Метод объемного интегрального уравнения используется для расчета электромагнитных экранов произвольной формы численными методами. Рассмотрим теперь простой пример получения аналитического решения. На рис. 15.1 представлен фрагмент плоского экрана из однородного немагнитного материала с комплексной диэлектрической проницаемостью er.
 |
Рис. 15.1. Фрагмент плоского экрана
Уравнение для рассматриваемого случая имеет вид:
, (1)
где интегрирование распространяется на весь объем плоского слоя 0< z < d (d - толщина экрана), а R в аргументе функции Грина – расстояние от точки наблюдения 
до точки интегрирования 
(, ÎVэ). Интегрирование удобно вести в цилиндрических координатах с началом в точке наблюдения:
r=|x-xv|2+|y-yv|2, 
.
Ограничимся случаем нормального падения плоской волны на поверхность экрана z=0:
. (2)
Решение ищем в виде суперпозиции двух плоских волн внутри слоя:
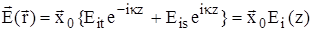. (3)
Интеграл (1) с учетом введенных переменных и представления решения в форме (3) можно записать в виде:
. (4)
Внутренний интеграл вычисляется аналитически. G(R) (
) от угловой координаты не зависит.
. (5)
Для преодоления неопределенности при подстановке верхнего предела можно применить принцип предельного поглощения. Это означает, что все соотношения рассматриваются при комплексной диэлектрической проницаемости 
, а в конечных формулах осуществляется конечный переход a®0. Благодаря этому в (16.5) подстановка верхнего предела дает нуль, поскольку волновое число ке содержит небольшую отрицательную мнимую составляющую, и результат интегрирования оказывается равным:
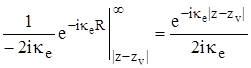. (6)
Интеграл (4) зависит от поперечных координат и оператор div в (1) равен нулю и поэтому само это уравнение превращается в скалярное относительно проекций полей на ось x:
. (7)
Для нахождения неизвестных амплитуд Eit и Eis в выражение для внутреннего поля Ei(z) следует подставить (3) в (7). Область интегрирования по zv необходимо разбить на две части: zv<z и zv>z.
. (8)
Последовательно получим значения отдельных интегралов:
(9)
(10)
Складывая (9) и (10) и проводя элементарные преобразования, значение (16.8) можно записать в виде:
(11)
(0<z<d)
Т.е. интегрирование восстанавливает с точностью до постоянного множителя внутреннее поле, Ei(z) и дает дополнительно две волны, распространяющиеся во внешней среде в положительном и отрицательном направлении оси z. Можно увидеть, что подстановка в (7) приводит к сокращению Ei(z) в уравнении. Оно превращается в функциональное уравнение:
(12)
В этом уравнение постоянные коэффициенты при двух линейно независимых функциях exp(-ikez) и exp(ikez) должны быть равны нулю. Отсюда следует следующая система двух линейных уравнений относительно неизвестных коэффициентов Eit и Eis:
(k + ke)Eit - (k - ke)Eis= 2keE0t,
(13)
(k - ke)e-ikd Ei t – (k + ke)Eiseikd = 0,
решение которой дает следующие значения неизвестных коэффициентов Eit и Eis:
, (14)
. (15)
Интересно, что если бы решение данной задачи осуществлялось на основе обычного подхода с использованием граничных условий непрерывности касательных составляющих электрического и магнитного поля на границах раздела сред z = 0 и z = d, то пришлось бы решать систему четырех уравнений с четырьмя неизвестными. Т.е. использование интегрального уравнения приводит к сокращению размерности задачи, хотя за это приходится платить некоторой предварительной процедурой вычисления интегралов.
По вычисленному внутреннему полю, можно найти поле, рассеиваемое экраном как в области z < 0 (перед экраном). Так и z ³ d (за экраном). Поле за экраном складывается из поля Е0 и поля Ees, рассеиваемого экраном:
. (16)
Поле Ees вычисляется по формуле:
(17)
Подставляя сюда выражения для коэффициентов (14) и (15) получим:
. (18)
Полное поле за экраном после подстановки (18) в (16) окончательно запишется таким образом:
. (19)
Можно показать, что с учетом магнитных свойств формула усложняется незначительно:
. (20