Процесс доказательства методом резолюций.

Используется доказательство методом от противного. Отрицание заключения принимается в качестве дополнительной посылки.

1. Все посылки и отрицания заключения привести к нормальной форме. Для этого используются следующие равносильности:

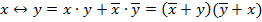
При необходимости применяются законы де Моргана:

.

2. Все полученные в 1–м пункте дизъюнкты записываются с новой строки (включая отрицание заключения). В результате получается последовательность формул или последовательность дизъюнктов.

3. В полученной последовательности находим любые две формулы, в одной из которых находится атом, а в другой отрицание атома. Положение атомов в формуле роли не играет. Эти две формулы соединяем с помощью правила резолюций и получаем новую формулу без этого атома.

4. Затем ищут следующую пару формул аналогичным образом, в одной из которых атом, а в другой отрицание, и соединяют эти две формулы с помощью правила резолюций и т.д.

Аналогичным образом продолжают до тех пор, пока не появится пустой дизъюнкт □, который и выражает противоречие.

Преимущества использования правила резолюций:

1) В этом методе используется лишь одно правило – это правило резолюций. Не надо запоминать многочисленные правила вывода и теоремы классического исчисления высказываний.

2) В процессе доказательства не надо использовать различные равносильности для проведения простых преобразований.

3) Метод прост в реализации.

Замечание. На основе этого правила разработан язык логического программирования – Пролог.

Пример. . Доказать выводимость.

1) ; ;

2) – гипотезы

Дизъюнкты: 1. ;

2. ;

3. ;

4. ;

5. ;

3) 6. (2, 4)

7. (3, 5)

8. (1, 6)

9 – ложь.

При практической реализации этого метода, несмотря на простоту метода доказательства, может возникнуть ряд проблем. Последовательность может содержать большое количество формул. Возникает проблема, какие формулы соединить с помощью правила резолюции и как быстрее достичь цели. Для решения этих проблем разработаны специальные методики поиска.

5. ЛОГИКА ПРЕДИКАТОВ

5.1. Определение предиката

Понятие предиката обобщает понятие высказывания, а логика предикатов представляет собой дальнейшее развитие логики высказываний.

Предикат – предложение, похожее на высказывание, но все же им не являющееся. Дадим определение предиката.

Определение 1. n – местным предикатом, заданным на множестве М ₁´ М ₂´…´ М_n называется выражение, содержащее n переменных x ₁, х ₂,..., х_n, которое становится высказыванием при подстановке вместо этих переменных элементов а ₁, а ₂,..., а_n, из множеств М ₁, М ₂,..., М_n соответственно.

Предикаты обозначаются как Р (х ₁, х ₂,..., х_n) и пред­ставляют собой отображения Р: М ₁´ М ₂´…´ М_n {0,1}. То есть, упорядоченному набору элементов (а ₁, а ₂,..., а_n) из множества М ₁´…´ М_n ставится в соответствие один из элементов множества {0,1}, причем 0, если Р (а ₁, а ₂,..., а_n) – ложное высказывание и 1, если истинное. Переменные х ₁, х ₂,..., х_n называются предметными, а элементы из множеств М ₁, М ₂, …, М_n, которые эти переменные пробегают – конкретными предметами. Местностью предиката называется число различных аргу­ментов, от которых зависит предикат. Предикат является функцией многих переменных.

Примеры

1. Предложение " х – четное число" представляет собой од­номестный предикат, заданный на множестве целых чисел, то есть Р: Z ®{0, 1}. Областью определения предиката Р является множе­ство целых чисел Z, областью значений – множество {0, 1}.

2. Отношения " х < у " и " х делится на у "представляют собой двуместные предикаты, заданные на множествах R ´ R и Z ´ Z соответственно.

Определение 2. Множеством истинности предиката Р (х ₁, х ₂,..., х_n), заданного на множестве М ₁´ М ₂´…´ М_n, называется совокупность таких упорядоченных наборов элементов (а ₁, а ₂,..., а_n) из М ₁´ М ₂´…´ М_n, для которых высказывание Р (а ₁, а ₂,..., а_n) является истинным.

Обозначение: P ⁺ ={(а ₁, а ₂,..., а_n): l (Р (а ₁, а ₂,..., а_n)) =1}.

Примеры.

1. Множеством истинности двухместного предиката Р (х, у):" х делится на у ", заданного на множестве М ´ М,
где М = {1, 2, 3, 4, 5, 6}, является следующее множество Р⁺ = {(1,1), (2,1), (3,1), (4,1), (5,1), (6,1), (4, 2), (6, 2), (6,3)}.

2. Множество истинности двуместного предиката Р (х,y): " x < у ", заданного на множестве М ₁´ М ₂, где М ₁ = {1, 2, 3}, М ₂ = {2, 4, 6}, равно P⁺ = {(1,2), (1,4), (1,6), (2,4), (2,6), (3,4), (3,6)}.

Определение 3. Два предиката Р (х ₁, х ₂,..., х_n) и Q (х ₁, х ₂,..., х_n), за­данные на одном и том же множестве М ₁´ М ₂´…´ М_n, называются равносильными, если оба предиката принимают истинные значения на одних и тех же наборах (а ₁, а ₂,..., а_n) из множества М ₁´ М ₂´…´ М_n, то есть, если Р⁺= Q⁺. Предикат Q (х ₁, х ₂,..., х_n), заданный на множестве М ₁´ М ₂´…´ М_n называется следствием предика­та Р (х ₁, х ₂,..., х_n), заданного на том же множестве, если он становится истинным высказыванием при всех значениях переменных х ₁, х ₂,..., х_n из соответствующих множеств М ₁, М ₂,..., М_n, при кото­рых истинным высказыванием становится предикат Р (х ₁, х ₂,..., х_n), то есть, если .

 

5.2. Логические операции над предикатами

Определение 4. Отрицанием предиката Р (х ₁, х ₂,..., х_n), заданного на множестве М ₁´ М ₂´…´ М_n, называется новый предикат (х ₁, х ₂,..., х_n), заданный на том же множестве, который становится истинным высказыванием при таких значениях (а ₁, а ₂,..., а_n) из множества М ₁´ М ₂´…´ М_n, при которых Р (а ₁, а ₂,..., а_n) является ложным высказыванием и становится ложным высказыванием, если Р (а ₁, а ₂,..., а_n) является истинным высказыванием.

Например, отри­цанием одноместного предиката Р(х): " х делится на 3", заданного на множестве М = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} будет предикат : " х не делится на 3". Множествами истинности предикатов Р и яв­ляются следующие множества Р⁺ = {0, 3, 6, 9}, ()⁺ = {1, 2, 4, 5, 7, 8}.

Множество истинности предиката является дополнением множества Р⁺ _,то есть (M – область определения предиката).

Определение 5. Конъюнкцией двух n –местных предикатов Р (х ₁, х ₂,..., х_n) и Q (х ₁, х ₂,..., х_n), заданных на множестве М ₁´ М ₂´…´ М_n, называется новый n –местный предикат Р (х ₁, х ₂,..., х_n) Q (х ₁, х ₂,..., х_n), который становится истинным высказыванием только для таких элементов (а ₁, а ₂,..., а_n) из множества М ₁´ М ₂´…´ М_n, для которых Р (а ₁, а ₂,..., а_n) и Q (а ₁, а ₂,..., а_n) являются истинны­ми высказываниями.

Определение 6. Дизъюнкцией двух n –местных предикатов Р (х ₁, х ₂,..., х_n) и Q (х ₁, х ₂,..., х_n), заданных на множестве М ₁´ М ₂´…´ М_n, называется новый n –местный предикат Р (х ₁, х ₂,..., х_n) Ú Q (х ₁, х ₂,..., х_n), который становится ложным высказыванием только для таких элементов (а ₁, а ₂,..., а_n) из множества М ₁´ М ₂´…´ М_n, для которых Р (а ₁, а ₂,..., а_n) и Q (а ₁, а ₂,..., а_n) являются ложными высказываниями.

Определение 7. Импликацией двух n –местных предикатов Р (х ₁, х ₂,..., х_n) и Q (х ₁, х ₂,..., х_n), заданных на множестве М ₁´ М ₂´…´ М_n, называется новый n –местный предикат Р (х ₁, х ₂,..., х_n) Q (х ₁, х ₂,..., х_n), который становится ложным высказыванием только для таких элементов (а ₁, а ₂,..., а_n) из множества М ₁´ М ₂´…´ М_n, для которых Р (а ₁, а ₂,..., а_n) является истинным высказыванием, а Q (а ₁, а ₂,..., а_n) является ложным. В остальных случаях – истинным.

Определение 8. Эквивалентностью двух n –местных предикатов Р (х ₁, х ₂,..., х_n) и Q (х ₁, х ₂,..., х_n), заданных на множестве М ₁´ М ₂´…´ М_n, называется новый n –местный предикат Р (х ₁, х ₂,..., х_n) Q (х ₁, х ₂,..., х_n), который становится истинным высказыванием только для таких элементов (а ₁, а ₂,..., а_n) из множества М ₁´ М ₂´…´ М_n, для которых высказывания Р (а ₁, а ₂,..., а_n) и Q (а ₁, а ₂,..., а_n) ли­бо одновременно являются истинными, либо ложными. В остальных случаях – ложным.

Если предикаты Р (х ₁, х ₂,..., х_n) и Q (y ₁, y ₂,..., y_m) заданы на разных множествах, то в результате применения операций конъюнк­ции, дизъюнкции, импликации и эквивалентности к этим предика­там, получим (n + m – k)–местный предикат, где k – число переменных, общих для обоих предикатов.

 

Кванторные операции

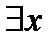Кроме операций отрицания, конъюнкции, дизъюнкции, им­пликации и эквивалентности в логике предикатов имеются две кванторные операции: квантор всеобщности () и существования (). Если Р(х) одноместный предикат, заданный на некотором множестве М, то в результате применения кванторов к предикату Р(х) получим новые предикаты P (x) и 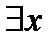Р (х), означающие соот­ветственно "все х из М обладают свойством Р "и "некоторые х из М обладают свойством Р ".

Пример 1. Пусть Р(х) одноместный предикат " х делится на 7", за­данный на множестве целых чисел Z. Применяя к этому предикату кванторы получим следующие предикаты: "все х из Z делятся на число 7" и "существуют х из Z, которые делятся на число 7". То есть, в результате применения кванторов () и (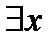) к одномест­ному предикату Р (х)получили высказывания, причем первое из них ложное, а второе – истинное. Высказывания являются нульместными предикатами.

Применение кванторов к предикатам понижает местность исходного предиката на единицу. Если Р (х ₁, х ₂,..., х_n) n –местный предикат, то в результате применения кванторов получим новые предикаты Q (х ₂,..., х_n)= Р (х ₁, х ₂,..., х_n), R (х ₂,..., х_n)= Р (х ₁, х ₂,..., х_n), которые зависят только от переменных х ₂, х ₂,..., х_n,то есть являются (n – 1)–мест­ными предикатами.

Предметная переменная, которая связывается квантором, то есть входит в предикат и в квантор, называется связанной. Предметная переменная, не связанная никаким квантором, называется свободной переменной.

Пример 2. Пусть Р (х, y)двухместный предикат, заданный неравенством " х ² + у ² 1" на множестве R ´ R. Множеством истинности преди­ката Р (х, y)является множество всех точек координатной плоскости, расположенных внутри окружности радиуса 1, включая точки ок­ружности. Найдем множества истинности предикатов Q (y)= x P (x, y), R (x)= у Р (х, у), S = x y P (x, y). Множеством истинно­сти предиката Q (y)является множество таких у, для которых данное неравенство выполняется при любых х из R. Однако таких у не су­ществует. Следовательно, множество истинности предиката Q не со­держит ни одного элемента, то есть Q⁺ = Æ. Множеству истин­ности предиката R (x)принадлежат все такие х, для которых можно найти число у, удовлетворяющее данному неравенству. Такие зна­чения х лежат в промежутке [–1, 1]. Следовательно, этот промежуток и будет множеством истинности предиката R. Предикат S – нульместный, то есть является высказыванием. В высказывании S говорится, что для любых х можно найти такое у, для которой выполняется данное неравенство. Однако это не верно. Например, для х,лежащих вне отрезка [–1, 1], такое у не существует. Тогда S – ложное выска­зывание.

5.3. Теоретико–множественный смысл предикатов

При определении множества истинности предиката, составленного из нескольких предикатов при помощи логических связок, можно воспользоваться соотношениями для их множеств истинности. Для двух n –местных предикатов Р (х ₁, х ₂,..., х_n) и Q (х ₁, х ₂,..., х_n) задан­ных на множестве М ₁´ М ₂´…´ М_n, верны следующие соотношения для их множеств истинности:

1) множество истинности отрицания предиката Р равно дополнению множества истинности этого предиката, то есть ;

2)множество истинности конъюнкции двух предикатов Р и Q рав­но пересечению множеств истинности Р⁺ и Q⁺, то есть ;

3) множество истинности дизъюнкции двух предикатов Р и Q рав­но объединению множеств истинности Р⁺ и Q⁺, то есть ;

4) множество истинности импликации двух предикатов Р и Q равно ;

5) множество истинности эквивалентности двух предикатов Р и Q равно .

Пример. Пусть предикаты Р (х):" х кратно двум" и Q (x): " х кратно трем", заданы на множестве М = {1, 2, 3, 4, 5, 6, 7, 8}. Их множествами истинности являются следующие множества: Р⁺ = {2, 4, 6, 8}, Q⁺ = {3, 6}. Тогда, по соотношениям (1)–(5) получим

а) {1, 3, 5, 7}, {l, 2, 4, 5, 7, 8};

б) {3, 6} = {6};

в) = {2, 4, 6, 8} {3,6}= {2, 3, 4, 6, 8};

г) ={1, 3, 5, 7} {3,6} ={1, 3, 5, 6, 7};

д) ={1, 3, 5, 6, 7} {1, 2, 4, 5, 6, 7, 8}= {1,5,6,7}.

 

5.4. Классификация предикатов

Определение 9. Предикат Р (х ₁, х ₂,... х _n), заданный на множестве М ₁´ М ₂´…´ М_n, называется тождественно истинным, если для всех элементов (а ₁, а ₂,..., а_n) из множества М ₁´ М ₂´…´ М_n высказывания Р (а ₁, а ₂,..., а_n) будут истинными и тождественно ложным, если для всех элементов (а ₁, а ₂,..., а_n) из множества М ₁´ М ₂´…´ М_n, выска­зывания Р (а ₁, а ₂,..., а_n) будут ложными. Предикат Р (х ₁, х ₂,... х _n), за­данный на множестве М ₁´ М ₂´…´ М_n, называется выполнимым, если существует хотя бы один элемент (а ₁, а ₂,..., а_n) из множества М ₁´ М ₂´…´ М_n, для которого высказывание Р (а ₁, а ₂,..., а_n) будет ис­тинным и опровержимым, если хотя бы для одного элемента (а ₁, а ₂,..., а_n) из множества М ₁´ М ₂´…´ М_n высказывание Р (а ₁, а ₂,..., а_n) будет ложным.

В соответствии с классификацией предикатов истинность нульместных предикатов, содержащих кван­торы, можно определить следующим образом. Высказывание " x P (x) будет истинным, если предикат Р (х)является тождественно истинным предикатом. В противном случае – ложным. Высказыва­ние $ х Р (х) будет истинным, если предикат Р (х) – является выпол­нимым и будет ложным в противном случае.

 

5.5. Формулы логики предикатов.
Равносильность формул

Определение формулы логики предикатов имеет индуктивный ха­рактер. Сначала задается алфавит символов, из которых составляются формулы:

– предметные переменные: х, у, z, x_i, y_i, z_i ();

– нульместные предикатные переменные: Р, Q, R, Р_i, Q_i, R_i,

(i N);

– n –местные () предикатные переменные: Р (,...,), Q (,...,), R (,...,), Р_i (,...,), Q_i (,...,), R_i (,...,) (i N) с указанием числа свободных мест в них;

– символы логических операций: ;

– кванторы: ", $;

– вспомогательные символы: (,) – скобки;, – запятая.

Определение 10. (формулы логики предикатов).

1. Каждая нульместная предикатная переменная есть формула.

2. Любой n –местный предикат Р (х ₁, х ₂,..., х_n) есть формула.

3. Если F, G – формулы, не содержащие предметных перемен­ных, которые связаны квантором в одной формуле и свободны в другой, то выражения (), (F Ù G), (F Ú G), (F ® G), (F «G) также являются формулами.

4. Если F формула, а х – предметная переменная, входящая сво­бодно в F, то выражения " x F (x) и $ x F (x) также являются формулами.

5. Никаких других формул в логике предикатов нет.

 

Формулы, в которых нет свободных переменных, называются замкнутыми, а формулы, содержащие свободные переменные, – открытыми.

Из определения формулы логики предикатов следует, что все фор­мулы алгебры высказываний являются также формулами логики предикатов.

Определение 11. Две формулы F и G называются равносильными, если при подстановке в эти формулы вместо предикатных перемен­ных конкретных предикатов, а вместо предметных переменных конкретных элементов, эти формулы преобразуются в высказывания с одинаковыми логическими значениями, то есть либо оба в ис­тинные высказывания, либо оба в ложные.

Все основные равно­сильности логики высказываний верны также и для формул логики предикатов. Кроме них, в логике предикатов имеются равносильности, связанные с кванторами:

1. Законы отрицания: , .

2. Законы дистрибутивности:

;

.

3. Если предикат Q не зависит от переменной х, то верны сле­дующие законы:

, ;

, .

4. Законы переименования связанных переменных:

, .

5. Законы перестановки кванторов:

, .

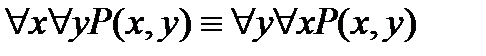5.6. Классификация формул логики предикатов

Определение 12. Формула F логики предикатов называется выпол­нимой (опровержимой) на множестве М, если можно найти такие конкретные предикаты, заданные на том же множестве, при подста­новке которых вместо предикатных переменных, она преобразуется в выполнимый (опровержимый) предикат. Формула логики преди­катов называется тождественно истинной (тождественно лож­ной) на множестве М, если при подстановке вместо предикатных пе­ременных любых конкретных предикатов, заданных на этом же множестве, она преобразуется в тождественно истинный (тождест­венно ложный) предикат. Формула логики предикатов называется тавтологией (противоречием), если при подстановке вместо преди­катных переменных любых конкретных предикатов, заданных на любом множестве, она преобразуется в тождественно истинный (тождественно ложный) предикат.

Критерием равносильности формул F и G является тавтологичность формулы (F «G).

Пример 1. Вычислить значение формулы , если предикат имеет значение – «число x меньше числа y » и определен на множестве , N = .

Так как при указанном значении предиката высказывание означает утверждение, что «для любого натурального числа x найдется натуральное число y, большее числа x », то это высказывание истинно. Высказывание означает утверждение, что «существует натуральное число x, которое меньше любого натурального числа y ». Это высказывание ложно. Поэтому получаем, что исходная формула ложна.

Пример 2. Доказать, что формула выполнима.

Для доказательства выполнимости формулы A достаточно найти область определения двухместного предиката и такое его значение, что в этой области формула принимает истинные значения. Такой областью определения предиката, в частности, будет множество . Действительно, если - предикат «y< x », то формула A тождественно истинна в области М, и, следовательно, выполнима в этой области. Однако, если в качестве предиката взять предикат «x< y », то формула A будет тождественно ложной в области М и, следовательно, невыполнимой в области М. При этом ясно, что формула A не общезначима.

Пример 3. Доказать, что формула является общезначимой.

Считая, что формула A определена на любой области M, проведем равносильные преобразования:

.

То есть формула A тождественно истинна для любых одноместных предикатов 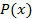и и в любой области.

Пример 4. Доказать, что формула тождественно ложна.

Так как формула , а формула , очевидно, тождественно ложна, то ложна и формула A.

Определение 13. Формула F', равносильная F, называется ее при­веденной формой, если F' из логических связок содер­жит только отрицание, конъюнкцию и дизъюнкцию, а отрицание относится только к предикатным переменным и к высказываниям. Предваренной нормальной формой (ПНФ) фор­мулы F называется такая ее приведенная форма, в которой все кванторы вынесены в начало формулы, а область действия каждого квантора распространяется до конца формулы.

ПНФ – это формула вида , где – один из кванторов " или $ (), а формула F не содержит кванторов и является приведенной формой.

Для формул логики предикатов справедлива следующая теорема.

Теорема. Для каждой формулы логики предикатов существует равносильная ей ПНФ.

Предваренные нормальные формы формул в логике предикатов используются для выяснения равносильности формул и для решения проблемы классификации формул.

Одной из задач классификации формул является проблема разрешимости, которая состоит в следующем. Необходимо найти алгоритм, при помощи ко­торого для произвольной формулы логики предикатов можно опре­делить, будет она тавтологией или нет. В отличие от алгебры выска­зываний, для формул логики предикатов общего алгоритма не су­ществует. Это было доказано в 1936 году американским математиком А. Чёрчем. Несмотря на отсутствие алгоритма в общем случае, в неко­торых частных случаях такой алгоритм существует. Например, для формул, содержащих только одноместные предикаты.

6. ИСЧИСЛЕНИЕ ПРЕДИКАТОВ (ИП)

Понятие формулы в ИП вводится так же, как оно вводилось в логике предикатов.

Аксиоматическая теория начинается с выбора системы аксиом. Как и в случае высказываний, этот выбор может быть осуществлен по-разному. Одной из таких систем аксиом может служить система, состоящая из трех аксиом рассмотренного выше формализованного исчисления высказываний и двух дополнительных аксиом (схем аксиом):

(P1) ;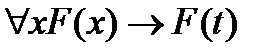

(P2) ,

где формула t не содержит свободной переменной x.

К правилу вывода modus pones (MP) добавляются еще два правила вывода:

	– правило введения квантора общности ("–правило);
	– правило введения квантора существования ($– правило),

где х не входит свободно в формулу F.

Понятия вывода и теоремы определяются аналогично соответствующим понятиям исчисления высказываний.

Возможны и другие системы аксиом и правил вывода.

Рассмотрим пример вывода в исчислении предикатов.

Пример. Доказать, что

.

Решение. Построим вывод второй формулы из первой:

 

7. ЗАДАЧИ

ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Задача 1

Решить системы логических уравнений:

1. а) б)

2. а) б)

3. а) б)

4. а) б)

5. а) б)

6. а) б)

7. а) б)

8. а) б)

9. а) б)

10. а) б)

11. а) б)

12. а) б)

13. а) б)

14. а) б)

15. а) б)

16. а) б)

17. а) б)

18. а) б)

19. а) б)

20. а) б)

21. а) б)

22. а) б)

23. а) б)

24. а) б)

25. а) б)

Пример. Решить систему логических уравнений:

Решение: Первый способ. Решаем первое уравнение системы. Отыскав все реше­ния первого уравнения, выбираем из них те, которые удовлетворяют вто­рому уравнению.

.

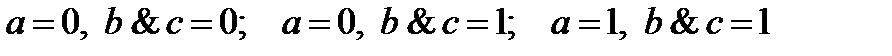Отсюда решениями первого уравнения будут

1) а = 0, b = 0, c = 0; 2) а = 0, b = 0, c = 1;

3) а = 0, b = 1, c = 0; 4) а = 0, b = 1, c = 1;

5) а = 1, b = 1, c = 1.

Подставив найденные решения во второе уравнение, найдем решение системы

1) 0 Ú 0 «0 = 1 ¹ 0; 2) 0 Ú 0 «1 = 0 = 0;

3) 0 Ú 1 «0 = 0 = 0; 4) 0 Ú 1 «1 = 1 ¹ 0;

5) 1 Ú 1 «1 = 1 ¹ 0.

Таким образом, решениями системы будут второе и третье решения первого уравнения, то есть

а = 0, b = 0, c = 1; а = 0, b = 1, c = 0.

Второй способ. Строим таблицы истинности для левых частей первого и второго уравнений и подчеркиваем строки, в которых их значения совпа­дают с соответствующими значениями правых частей уравнений.

a	b	c	(1) b & c	a ® (1)	(2) a Ú b	(2)«b
0	0	1
0	1	0

Поделиться: