Задание №2. Оптимизация динамических систем

Задание №1. Интерполяция

1. Сконструировать произвольную функцию 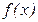, непрерывную на интервале . Создать два вектора и , где – случайное число, равномерно распределенное на отрезке .

2. По исходным данным построить интерполяционный полином Лагранжа. Построить графики исходных данных и полинома Лагранжа. Протабулировать полином Лагранжа на промежутке в девяти равноотстоящих точках.

2. По исходным данным провести линейную интерполяцию. Построить графики исходных данных и интерполяционной функции. Найти значение интеграла в пределах от интерполяционной функции.

3. Интерполировать исходные данные с помощью кубических сплайнов с использованием функций lspline, pspline, cspline. Построить графики исходных данных и интерполяционных функций. Экстраполировать значение функции в точке .

Решение

Зададим функцию

Создадим два вектора

 

 

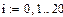
, где – случайное число, равномерно распределенное на отрезке .

Построим график исходных данных

 

Рис. 1. Исходные данные

 

Создадим функцию, определяющую интерполяционный полином Лагранжа:

 

Построим графики исходных данных и полинома Лагранжа.

Рис. 2. Интерполяционный полином Лагранжа

Протабулируем полином Лагранжа на промежутке [0,2] в девяти равноотстоящих точках табулированием

 

 

Проведем линейную интерполяцию с помощью функции linterp(x,y,t), где

x – вектор действительных значений аргумента (обязательно должны идти в порядке возрастания );

y – вектор действительных значений данных той же размерности;

t – значение аргумента, при котором вычисляется интерполяционная функция.

 

Построим графики исходных данных и интерполяционной функции.

Рис. 3. Линейная интерполяция

Рис. 3. Линейная интерполяция

Найдем значение интеграла в пределах[0,2] от интерполяционной функции.

 

 

Для интерполяции сплайнами используется функция interp. Перед применением функции interp необходимо предварительно определить пер­вый из ее аргументов — векторную переменную s.

Делается это при помощи одной из трех встроенных функций тех же аргументов (х, у):

• lspline (х, у) — вектор значений коэффициентов кубического сплайна с интерполяцией линейными функциями на граничных точках;

• pspline (х, у) — вектор значений коэффициентов кубического сплайна с интерполяцией квадратичными функциями на граничных точках;

• cspline(х,у) — вектор значений коэффициентов кубического сплайна с интерполяцией кубическими функциями на граничных точках:

Выбор конкретной функции сплайновых коэффициентов влияет на интерпо­ляцию вблизи конечных точек интервала.

Интерполируем исходные данные с использованием сплайнов:

 

Рис. 4. Сплайновая интерполяция

Экстраполируем значение функции в точке

 

 

Задание №2. Оптимизация динамических систем

Пусть дан объект, динамика которого определяется функцией:

Построить частотные характеристики данного объекта: КЧХ , ФЧХ и АЧХ . Найти частоту , начиная с которой АЧХ , найти значение ФЧХ при этой частоте. Для замкнутой системы с интегральным регулятором (T – варьируемый параметр настройки регулятора), передаточная функция по внутреннему каналу действия возмущения принимает вид . Построить график КЧХ системы при T=10: . Определить такое значение параметра настройки регулятора T, при котором интегральный квадратичный критерий качества регулирования системы принимает минимальное значение → min. Построить график , показать на нем минимальное значение и значение Т, на котором оно достигается.

 

Решение

Пусть дан объект, динамика которого определяется функцией:

Зададим функцию и определим все частотные характеристики:

 

 

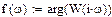
Построим график КЧХ динамического объекта

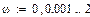
Рис. 5. КЧХ динамического объекта

 

 

Построим АЧХ и ФЧХ динамического объекта

Рис. 6. АЧХ и ФЧХ динамического объекта

 

Определим частоту и значение . Для чего по графику определим начальное приближение к корню:

 

Определим передаточную функцию замкнутой системы по внутреннему каналу действия возмущения с интегральным регулятором (T – варьируемый параметр настройки регулятора):

 

 

Построим график КЧХ замкнутой системы:

 

 

Рис. 7. График КЧХ замкнутой системы

Построим график интегрального квадратичного критерия качества регулирования системы → min.

 

 

 

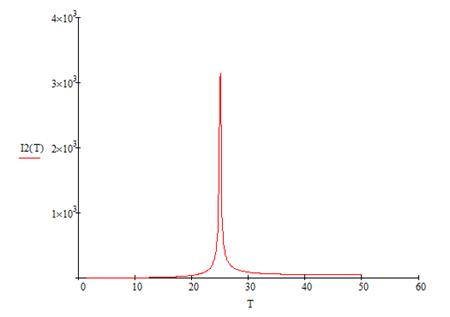
Рис. 8. График интегрального квадратичного критерия качества регулирования

Задание №3. Двумерная аппроксимация

Получить экспериментальные значения в матрице М размерностью 5х5: , где – случайное возмущение, и , , где значения параметров взять произвольно. Построить аппроксимацию данных моделью . Определить невязку и сравнить исходные значения параметров модели и полученные в ходе аппроксимации.

 

Решение

Получим экспериментальные данные в матрице M:

 

 

 

 

 

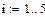
Зададим функцию невязки по узлам аппроксимации:

 

 

Зададим начальные значения искомых коэффициентов и найдем минимум функции невязки

 

 

 

 

 

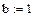
Постоим аппроксимирующую функцию

 

 

 

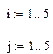
Рис. 9. Двухмерная аппроксимация