Косвенные показатели качества

К косвенным показателям качества относят корневые, частотные и интегральные.

Наиболее важными и одновременно удобными косвенными показателями являются частотные показатели, которые определяются по частотным характеристикам замкнутого и разомкнутого контура системы.

По амплитудной частотной характеристике А(w) замкнутой системы (рис. 7.9) оценивают частотный показатель колебательности М = А_m /А(0). Чем больше это отношение, тем больше перерегулирование и, как следствие, больше длительность переходного процесса. Качество системы управления обычно считается удовлетворительным, если М = 1,1 – 1,5.

Рис. 7.9

По этой характеристике определяют характерные частоты: резонансную частоту w₀, полосу пропускания (0 – ω_п) рабочий диапазон частот w_Р @ 3 w_п, которые служат косвенными показателями быстродействия системы.

По АФЧХ разомкнутого контура определяют запас устойчивости по амплитуде DА = 1 – А(w_p) и запас устойчивости по фазе , которые вместе характеризуют удалённость кривой W(jw) от критической точки (-1, j0). При проектировании систем обычно задаются запасом устойчивости по амплитуде DА = 0,5 – 0,6 и по фазе Dj ³ 30 – 60^о. При этом обеспечивается, как правило, и удовлетворительное качество процесса управления.

Запас устойчивости по амплитуде и фазе удобнее определять по логарифмическим амплитудным характеристикам.

Перерегулирование и длительность переходного процесса можно оценить с помощью вещественной частотной характеристики P(ω)- рис. 7.10. Начальное значение переходной функции , а установившееся значение переходной функции . Перерегулирования в системе рассчитывается по формуле

Рис. 7.10

Время переходного процесса в системе определим по соотношению

Если известны корни характеристического уравнения, то можно рассчитать среднее геометрическое значение модулей корней

Чем меньше a₀, тем ближе созвездие корней к мнимой оси и тем больше длительность переходного процесса. Так как а₀ = 1 + k или k, то чем больше k, тем лучше быстродействие системы. Таким образом, данный параметр может служить некоторой мерой быстродействия системы или её полосы пропускания.

Основное влияние на характер переходного процесса оказывают корни, расположенные ближе к мнимой оси, которые дают наиболее длительные составляющие переходного процесса и называются доминирующими. Расстояние от мнимой оси до ближайшего корня (рис. 7.11) называется степенью устойчивости и обозначается h. Длительность переходного процесса определяется приближённой формулой t_п £ 3 / h.

Рис. 7.11

Колебательные свойства системы регулирования предопределяет та пара комплексных корней s_{к, к+1} = - a_к ± jw_к, для которой отношение

w_к /a_к имеет наибольшее по модулю значение. Такая пара корней также называется доминирующей и отношение называется степенью колебательности. Величина 1/m_Д = m_Д называется корневым показателем колебательности. При выборе настроек регуляторов стремятся получить значение m_Д = 0,2 – 0,5.

Установлено, что в системе любого порядка наиболее быстрый апериодический переходный процесс имеет место, когда все n корней равны между собой. Максимальное быстродействие достигается при перерегулировании s £ 10%. Для этого все корни (как вещественные, так и комплексные) должны располагаться на одинаковом расстоянии h от мнимой оси, а мнимые части должны образовывать арифметическую прогрессию с разностью Dw = w₁. Причём для каждого порядка уравнения существует оптимальное отношение Dw/h:

n = 2 ® 1; n = 3 ® 1,45; n = 4 ® 0,79; n = 5 ® 1,5.

В заключении отметим, что наличие нулей передаточной функции замкнутой системы способствует увеличению перерегулирования, колебательности и уменьшению длительности переходного процесса.

 

7.4. Интегральные показатели качества.

Прямые и косвенные показатели качества характеризуют лишь одно какое-либо свойство системы, которые в совокупности носят противоречивый характер. Поэтому в инженерной практике применяются интегральные критерии качества. Подинтегральная функция выбирается таким образом, чтобы интеграл наилучшим образом характеризовал качество системы и выражался (если это возможно) через коэффициенты передаточной функции замкнутой системы. Чтобы интеграл был сходящимся, в подинтегральную функцию вводят не абсолютные значения е(t) и х(t), а их отклонения от конечных, установившихся значений.

Наибольшее распространение получили:

- линейная интегральная оценка

- модульная интегральная оценка

- улучшенная модульная оценка

- квадратичная интегральная оценка

- улучшенная квадратичная интегральная оценка

- интегральная оценка качества от квадратичных форм

Последний критерий обеспечивает наиболее плавные и быстрые переходные процессы, так как слагаемые подинтегрального выражения запрещают большие отклонения, скорости и ускорения выходной координаты от заданной.

Эти же критерии используются и для определения оптимальных значений настроечных параметров регуляторов системы.

 

7.5. Приближённая оценка качества по частотным

характеристикам модели второго порядка.

Приближённую оценку прямых показателей качества удобно осуществлять на основе гипотезы об эквивалентности динамических свойств реальной замкнутой системы W (s) свойствам колебательного звена второго порядка с передаточной функцией

при x £ 0,707 и передаточным коэффициентом k = 1 для астатических и близким к единице для статических систем. При этом частотные характеристики системы и модели должны совпадать (или по крайней мере должны быть близки друг к другу) на нулевой частоте, резонансной и в рабочем диапазоне частот.

Так как при синтезе АСР всегда стремятся показатели качества замкнутой системы оценивать по характеристикам разомкнутого контура, которые более просты и выбираются разработчиком, то для модели замкнутой системы желательно найти модель разомкнутого контура, при замыкании которого единичной жесткой отрицательной обратной связью получилось колебательное звено второго порядка (рис. 7.12).

Рис. 12

Таким звеном является реальное интегрирующее звено, передаточная функция которого

Передаточная функция замкнутой системы

где - собственная частота колебаний системы, - коэффициент затухания.

Такой подход позволяет оценивать динамические свойства реальных систем по приближённым формулам

s @ 0,2 sqrt(кТ₁); t_p @ 6T₁; M @ 1,1 sqrt(кТ₁); Dj @ 0,2/s;

w_p @ sqrt (кТ₁ – 0,5) /T₁.

Эти формулы обеспечивают достаточную для инженерных расчетов точность оценки качества реальной системы.

Кривые переходных процессов при ξ =0,5;0,707 и 1 приведены на рис. 13.

Рис. 7.13

Если реальная система астатическая и содержит одно идеальное интегрирующее и n апериодических звенев первого порядка с коэффициентами передачи k_i и постоянными времени Т_i, то

Аппроксимированная передаточная функция имеет ряд свойств, тождественных точной передаточной функции W(s) при оптимальной настройке. Как у той, так и у другой равны три первых временных момента для импульсной реакции, поскольку их значения определяются только коэффициентами до s² включительно. Равенству этих моментов соответствует равенство коэффициентов ошибок по положению, скорости и ускорению.

Будем считать, что входное воздействие или нагрузка изменяется по закону степенной функции х_З(t) = Аt^q, где q = 0, 1, 2, … - показатель степенного воздействия. При q = 0 получаем ступенчатое входное воздействие, если q =1, то линейно возрастающий сигнал. Сравнение этого показателя с астатизмом системы γ = γ_Р + γ_О позволяет сформулировать следующие правила:

- если порядок астатизма γ = q, то система в установившемся режиме имеет ошибку воспроизведения ε_З = Аq!/ k = const;

- постоянная ошибка подавления ε_В, возникающая в установившемся режиме при q = γ_Р, где γ_Р – порядок астатизма регулятора, обратно пропорциональна передаточному коэффициенту регулятора;

- если порядок астатизма регулятора γ_Р > q, то установившиеся значения ошибок по заданию и по возмущению в установившемся режиме равны нулю;

- если порядок астатизма γ < q, то эти ошибки стремятся к бесконечности;

- точность воспроизведения системой управления задающего воздействия и точность подавления внешних воздействий тем лучше, чем больше передаточный коэффициент регулятора.

 

7.6. Исследование качества САР в MATLAB.

Показатели качества систем управления целесообразно определять с помощью MATLAB.

Пример: рассмотрим замкнутую систему управления с передаточной функцией

Её можно рассматривать как последовательное соединение инерционного форсирующего звена

и колебательного звена второго порядка

с частотой собственных колебаний с^-1 и коэффициентом затухания . Следовательно, можно оценить длительность переходного процесса

а перерегулирование

Эту величину рассчитаем в MATLAB:

>> e=0.667

e =

0.6670

>> p=100*exp((-e*pi)/(sqrt(1-e^2)))

p = 6.0057%

Время регулирования и перерегулирование, рассчитанное таким образом, справедливо и для колебательного звена второго порядка

.

Рассматриваемая система содержит инерционное форсирующее звено с преобладанием дифференцирующих свойств, поэтому перерегулирование должно быть больше и следует ожидать меньшее время переходного процесса.

При s = 0 и х_ВХ(t) = 1(t) Wz(0) =1 и ошибка установившегося режима равна 0. Эту же ошибку можно рассчитать при единичном ступенчатом входном воздействии на основании передаточной функции и теоремы операционного исчисления о предельном значении функции

Следовательно, система астатическая. Моделирование в MATLAB подтверждает полученные результаты:

>> W1=tf([1 3],[1 8])

Transfer function:

s + 3

-----

s + 8

>> W2=tf([96],[1 8 36])

Transfer function:

--------------

s^2 + 8 s + 36

>> W3=tf([36],[1 8 36])

Transfer function:

--------------

s^2 + 8 s + 36

>> Wz=W1*W2

Transfer function:

96 s + 288

--------------------------

s^3 + 16 s^2 + 100 s + 288

>> step(Wz,W3) – рис. 7.14 –переходные процессы

>> bode(Wz,W3) – рис. 7.15 – диаграмма Боде

>> pole(Wz)

ans =

-8.0000

-4.0000 + 4.4721i

-4.0000 - 4.4721i

Рис. 7.14

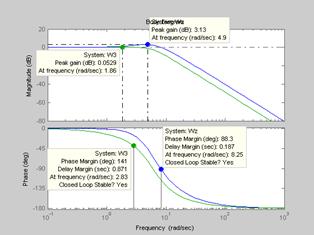
Рис. 7.15

Запас устойчивости по амплитуде и фазе рассчитаем с помощью оператора

>> [dL,dfi,omegapi,omegasr]=margin(Wz)

dL =

Inf - запас устойчивости по амплитуде

dfi =

88.2664 - запас устойчивости по фазе, , град

omegapi =

Inf - частота

omegasr =

8.2459 - частота

Пример: рассмотрим систему управления уровнем воды в баке [12, 13], состоящей из пропорционального регулятора

исполнительного механизма

звена транспортного запаздывания

резервуара

 

и поплавкового датчика уровня

Исследуем качество системы управления в среде MATLAB с учётом и без учёта запаздывания. Предварительно необходимо использовать аппроксимацию Паде с помощью функции [num, den]= pade(T,n), где Т – время запаздывания, n – порядок аппроксимации:

>> Wp=tf([0.25])

Transfer function:

0.25

>> Wim=tf([10],[1 1])

Transfer function:

-----

s + 1

>> [num,den]=pade(1,2)

num =

1 -6 12

den =

1 6 12

>> Wzap=tf([1 -6 12],[1 6 12])

Transfer function:

s^2 - 6 s + 12

--------------

s^2 + 6 s + 12

>> Wo=tf([3.15],[30 1])

Transfer function:

3.15

--------

30 s + 1

>> Woc=tf([1],[0.111 0.333 1])

Transfer function:

-----------------------

0.111 s^2 + 0.333 s + 1

>> Wrx=Wp*Wim*Wzap*Wo

Transfer function:

7.875 s^2 - 47.25 s + 94.5

---------------------------------------

30 s^4 + 211 s^3 + 547 s^2 + 378 s + 12

>> Wz=feedback(Wrx,Woc,-1)

Transfer function:

0.8741 s^4 - 2.622 s^3 + 2.63 s^2 - 15.78 s + 94.5

------------------------------------------------------------------------

3.33 s^6 + 33.41 s^5 + 161 s^4 + 435.1 s^3 + 682.1 s^2 + 334.7 s + 106.5

>> Wr=Wp*Wim*Wzap*Wo*Woc

Transfer function:

7.875 s^2 - 47.25 s + 94.5

-------------------------------------------------------------------

3.33 s^6 + 33.41 s^5 + 161 s^4 + 435.1 s^3 + 674.2 s^2 + 382 s + 12

Система без запаздывания

>> Wx=Wp*Wim*Wo

Transfer function:

7.875

-----------------

30 s^2 + 31 s + 1

>> Wxx=Wx*Woc

Transfer function:

7.875

----------------------------------------------

3.33 s^4 + 13.43 s^3 + 40.43 s^2 + 31.33 s + 1

>> W=feedback(Wx,Woc,-1)

Transfer function:

0.8741 s^2 + 2.622 s + 7.875

--------------------------------------------------

3.33 s^4 + 13.43 s^3 + 40.43 s^2 + 31.33 s + 8.875

Расчёт запасов устойчивости по амплитуде и фазе

>> [dL,dfi,omegapi,omegasr]=margin(Wr)

dL =

3.3586

dfi =

63.9355

omegapi =

0.7316

omegasr =

0.2532

>> [dL,dfi,omegapi,omegasr]=margin(Wxx)

dL =

9.5480

dfi =

78.4407

omegapi =

1.5272

omegasr =

0.2532

>> step(Wz,W) – рис. 7.16 – переходные процессы

Рис. 7.16

>> bode(Wr,Wxx) – рис. 7.17 – диаграмма Боде

Рис. 7.17

Результаты моделирования сведём в таблицу

Система	∆L, dB	∆φ,o	ωπ, c-1	ωcp, c-1	σ, %	tp, c	ε
без запаздывания	9,55	78,44	1,53	0,25	0,38	8,05	0,113
с запаздыванием	3,36	63,94	0,73	0,25	11,00	13,10	0,113

Моделирование в среде MATLAB+Simulink (рис.18) даёт аналогичные результаты.

Очевидно, что запаздывание вносит дополнительный отрицательный фазовый сдвиг и, следовательно, ухудшает устойчивость замкнутой системы. Запаздывание объективно присутствует во многих технических системах и для обеспечения заданных показателей качества приходится уменьшать общий передаточный коэффициент разомкнутого контура или применять специальные регуляторы - регуляторы Смита и Ресвика (рис. 7.18).