Множественной регрессией случайной переменной Y по переменным X 1, X 2,…, Xk называют условную среднюю (ожидание) M (Y/X 1= x 1, X 2= x 2,…, Xk = xk), она является функцией k переменных x 1, x 2,…, xk. В прикладном смысле Y – ценностный показатель, производственный, экономический или какой-либо иной, на который воздействуют другие переменные X 1, X 2,…, Xk, случайные или не случайные. При этом Y распадается в сумму двух составляющих, Y = f (X 1, X 2, …, Xk) + e. Первая составляющая f (X 1, X 2, …, Xk) детерминированная, однозначно определяется значениями x 1, x 2,…, xk переменных X 1, X 2, …, Xk, тогда как вторая составляющая e – стохастическая, выражает случайные возмущения и помехи, вносимые в Y неточностью вычислений или другими неучтенными факторами. Случайная величина e обычно считается нормальной с ожиданием 0 и дисперсией s2, e Î N (0, s). Задача регрессионного анализа состоит в том, чтобы по имеющейся (k+ 1)-мерной выборке (x 1 i , x 2 i ,…, xki, yi) i= 1, 2,…, n восстановить детерминированную часть случайной величины Y, зависящуюот x 1, x 2, …, xk, очистив её от возмущений и помех. Общий вид функции f, как правило, определяется теоретическими соображениями, её принадлежностью к какому-либо классу функций K, в то время как конкретный выбор функции f из класса K осуществляется подбором параметров, которые описывают этот класс. С учетом параметров b0, b1,…, b s регрессионная зависимость записывается в виде Y= f (x 1, x 2, …, xk, b0, b1,…, b s). Статистический материал всегда конечен и это не позволяет абсолютно точно из бесконечного множества возможных значений выбрать истинные значения параметров b0, b1,…,b s, для них возможны лишь хорошие статистические оценки b 0, b 1,…, bs. Поиск таких оценок b 0, b 1,…, bs. для параметров b0, b1,…,b s обычно осуществляется методом наименьших квадратов по многомерной выборке объема n для величин Yi, X 1 i , X 2 i , …, Xki (i= 1, 2, …, n). Для этого составляется функция F (b 0, b 1,…, bs) = S i { f (X 1 i , X 2 i , …, Xki, b 0, b 1,…, bs) – Yi }2, оценивающая расхождение между упомянутой выборкой и искомой функцией f, выбираемой из класса K. После чего минимизацией функции F по параметрам b 0, b 1,…, bs определяются их значения для эмпирического уравнения регрессии. Отсюда название метода наименьших квадратов. Минимум функции F достигается в её стационарной точке, где частные производные равны нулю, поэтому оценки b 0, b 1,…, bs ищутся решением системы k +1 уравнения
. (1).
Коэффициент 1/2 перед частными производными пишется во избежание многократных повторений в последующем множителя 2.
Ниже остановимся лишь на линейной регрессии вида Y= b0 + b1 X 1+… +b kXk. Соответствующие эмпирические оценки параметров b0, b1,…, b k обозначим b 0, b 1,…, bk. Функция F (b 0, b 1,…, bk) = S i {(b 0 +b 1 X 1 i +… +bkXki) – Yi }2,аравенства (1) принимают вид
(2)
(3)
Делением на объем выборки n обеих частей равенств (3) все суммы заменяем эмпирическими моментами.
(4)
Посредством первого уравнения 
исключаем параметр b 0 из всех остальных уравнений системы (4). Чтобы найти остальные параметры, выразим вторые центральные моменты через дисперсию и коэффициенты корреляции
, 
, 
.
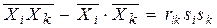В результате система линейных уравнений (4) относительно неизвестных b 0, b 1,…, bk приобретает более обозримый вид:
(5)
Определитель этой системы D ¹ 0 и потому через него и вспомогательные определители D1, D2, …D k решение системы можно выразить формулами Крамера b 1= D1/D, b 2= D2/D,…., bk= D k /D.
…………………………………………………………
Отсюда, b 1= 
: 
, ….
…………………………………………..
bk = 
: .
Вычислив свободный коэффициент b 0 = 
, составляем эмпирическое уравнение линейной регрессии и посредством его можем прогнозировать значения Y по заданным значениям X 1, X 2, …, Xn.
В частном случае множественной линейной регрессии Z = a + b X + g Y по двум переменным X, Y системы уравнений (1) – (5) принимают вид 
,
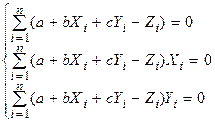(6)
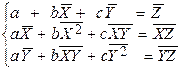
(7)
Решая систему уравнений (7), например по Крамеру, находим коэффициенты эмпирического уравнения регрессии Z = a + bX + cY.
. (8)
Меж тем к эмпирическому уравнению z = a + bx+ cy или, что то же самое, z= 
, надо относиться с определенной мерой осторожности, если его эмпирические коэффициенты регрессии b и c незначимы. Это тот случай, когда истинные коэффициенты регрессии, возможно равны нулю, b = 0 и g= 0, тогда как их приближенные не равные нулю значения b и c предсказывают рост или падение по соответствующей переменной X или Y. Незначимое уравнение регрессии не надежно для предсказаний и прогнозирования и не может быть использовано. Для решения проблемы значимости принимаем нулевую гипотезу H 0 как предположение о том, что в регрессионной зависимости Z = a+b X+ g Y +e оба коэффициента регрессии bи g перед X и Y равны нулю, b = 0 и g = 0. В этом случае на нормальную величину Z переменные X и Y не оказывают никакого влияния. Дисперсия DZ=D (e) = s2 и потому эмпирическая сумма ns 2/s2 распределена по закону хи-квадрат с n- 1 степенью свободы. Разложим эмпирическую дисперсию в сумму двух независимых составляющих
(9)
Сумма удвоенных произведений, появляющаяся при возведении в квадрат разностей, выделенных в (9) фигурными скобками, равна нулю. Этот факт является следствием условий (6) – применяемого здесь метода наименьших квадратов по подбору коэффициентов эмпирической регрессии. В равенствах (9) эмпирическая дисперсия s 2 распалась в сумму двух независимых частей – дисперсию регрессии 
и остаточную дисперсию 
. Первая отвечает встречной или алтернативной гипотезе H 1 ростом в ответ на проявление регрессионной зависимости. Вторая отражает чисто случайные отклонения, присущие любому статистическому материалу. Поскольку под знаком квадратов в n /s2 нормальные нормированные величины связаны тремя линейными равенствами (6), величина 
распределена по закону хи-квадрат с n- 3 степенями свободы. Сколько равенств связывает выборку значений нормальной величины Z, столько теряет степеней свободы из общего числа n квадратов. В разложении ns 2/s2= 
сумма и второе слагаемое является величиной хи-квадрат. Отсюда следует, что и другое слагаемое n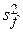 
/s2 тоже хи-квадрат и число степеней свободы для него равно разности степеней свободы для суммы ns 2/s2 и слагаемого 
. Из общего числа n- 1 независимых квадратов в ns 2/s2 вычитаем число n- 3 независимых квадратов в сумме и получаем для 
число степеней свободы 2. Поэтому частное
F (2, n‑ 3) = (n‑ 3)()/()/2=(n- 3) /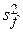 
распределено по Фишеру с 2 и n- 3 степенями свободы. Проверка значимости эмпирического уравнения регрессии осуществляется в следующем порядке. Выбирается уровень значимости a, ищется для него критическая точка t a, по имеющемуся статистическому материалу вычисляется статистика Фишера F = (n ‑ 3) 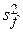/(2 ) и по тому выполнено ли неравенство F > t a или нет, значимость линейной регрессионной зависимости принимается или отвергается. При вычислении статистики Фишера коэффициент 1/ n, входящий, как в числитель 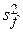, так и в знаменатель сокращается, поэтому на место 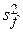и , в статистику Фишера можно непосредственно подставить величины
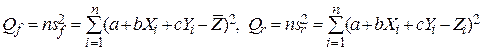(10)
и статистика Фишера запишется как F = (n ‑ 3) Qf /(2 Qr).