Курган 2015
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Цель работы:
1) Модельное изучение колебательного движения физических объектов.
2) Исследование движения тела под действием квазиупругой силы.
3) Экспериментальное определение зависимости периода и частоты колебаний от параметров системы.
Краткая теория
В физике при изучении реальных явлений, процессов и объектов их заменяют соответствующими физическими моделями, в которых рассматриваются только самые существенные свойства этих явлений, процессов или объектов и не рассматриваются, отбрасываются второстепенные свойства (в философии это называется абстракцией). Примерами физических моделей могут быть материальная точка, абсолютно твердое тело, идеальный газ и т.п. В данной работе изучаются математический маятники пружинный маятник– это модели объектов, в которых могут происходить гармонические колебания.
Математический маятник – это материальная точка (МТ), подвешенная на идеальной (невесомой и нерастяжимой) нити и совершающая колебания в вертикальной плоскости под действием силы тяжести.
Пружинный маятник – это материальная точка, прикрепленная к идеальной (невесомой и подчиняющейся закону Гука) пружине.
Компьютерная модель является виртуальной моделью реального физического явления. При этом отпадает необходимость в экспериментальной установке. Данная лабораторная работа проводится с компьютерными моделями «Свободные колебания (маятник)» (рис. 3.1) и «Свободные колебания (груз на пружине)» (рис. 3.2). Работая с моделями, Вы можете провести свое небольшое исследование. Можно менять значения параметров или конфигурацию модели и наблюдать за результатом.
Колебания - это любой физический процесс, характеризующийся той или иной повторяемостью во времени и пространстве. Такие процессы называются периодическими. Система, совершающая колебания называется колебательной.
Свободными (собственными) колебаниями называются колебания, которые происходят в отсутствие переменных внешних воздействий на колебательную систему. Вынужденными колебаниями называются колебания, возникающие в какой-либо системе под влиянием переменного внешнего воздействия.
Колебания называются периодическими, если значения всех физических величин, характеризующих колебательную систему и изменяющихся при ее колебаниях, повторяются через равные промежутки времени.
Наименьший промежуток времени T, через который значения таких величин повторяются, называется периодом колебаний. Период – время одного полного колебания. Полным колебанием называется минимальная часть периодического процесса, которая полностью повторяется. При периодических колебаниях зависимость колеблющейся величины s от времени t удовлетворяет условию s (t+T)= s (t).
Циклической (круговой) частотой называется скорость изменения фазы колебаний: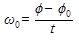 
.
Число полных колебаний, совершаемых колеблющейся величиной за единицу времени, называется частотой колебаний этой величины: 
.
Связь между циклической частотой и частотой: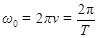 
.
Т.е. циклическая частота показывает, сколько полных колебаний совершается за 
секунд.
Периодические колебания величины s (t) называются гармоническими, если эта величина изменяется со временем по закону синуса или косинуса:
, (3.1)
или
, (3.1*)
где 
– собственная циклическая (круговая) частота гармонических колебаний; 
– максимальное значение колеблющейся величины s, называемое амплитудой колебаний; 
. Значение колеблющейся величины s в произвольный момент времени t определяется аргументом синуса или косинуса: величиной 
, которая называется фазой колебания. Начальной фазой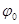 
колебания называется значение аргумента 
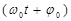гармонической функции при t= 0.
Колеблющаяся величина s может быть различной в зависимости от вида колебательной системы. Для конкретности рассмотрим колебания координаты x груза на пружине (пружинного маятника), подразумевая, однако, что во всех нижеследующих формулах вместо координаты x может быть какая-нибудь другая физическая величина, совершающая гармонические колебания (например, угол a отклонения математического маятника). Тогда для пружинного маятника формула (3.1*) примет вид:
. (3.2)
 |
Эта функция выражает закон движения материальной точки, совершающей гармонические колебания. График гармонических колебаний приведен на рисунке 3.1.
Рис.3.1
Проекция скорости груза и проекция его ускорения также совершают гармонические колебания той же частоты (будем для компактности обозначать производную по времени точкой над соответствующей буквой, вторую производную – двумя точками):
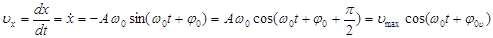; (3.3)
, (3.4)
где 
– амплитуда скорости; 
– амплитуда ускорения.
Из (3.3) и (3.4) видно, что фаза проекции скорости отличается от фазы координаты на величину p /2 (скорость опережает координату по фазе на p /2), а фаза проекции ускорения отличается от фазы координаты на p (ускорение опережает координату по фазе на p).
Выделив в (3.4) координату x (см. формулу (3.2)), получим
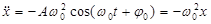. (3.5)
Таким образом, гармонически колеблющаяся координата x груза на пружине удовлетворяет дифференциальному уравнению
, (3.6)
являющимся уравнением движения материальной точки при гармонических колебаниях и называемому дифференциальным уравнением гармонических колебаний. Решением этого уравнения является функция (3.2).
Уравнение (3.6) можно получить из второго закона Ньютона 
. По закону Гука проекция силы упругости на ось x равна 
, где k – жесткость пружины. Тогда в проекциях на ось x
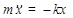, (3.7)
или
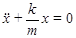. (3.8)
Сравнивая (3.8) и (3.6) получаем, что пружинный маятник совершает гармонические колебания по закону (3.2) с циклической частотой
, (3.9)
и периодом
. (3.10)
Силу упругости, действующую на груз на пружине с учетом (3.5) можно записать в виде
. (3.11)
Силы любой физической природы, пропорциональные смещению от положения равновесия и направленные к положению равновесия (в противоположную смещению сторону), называются квазиупругими.
Кинетическая энергия пружинного маятника в произвольный момент времени, с учетом (3.3) равна
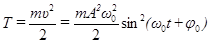, (3.12)
или, т.к. 
, получаем
. (3.13)
Потенциальная энергия пружинного маятника в произвольный момент времени, с учетом (3.11) и (3.2) равна
, (3.14)
или, т.к. 
, получается
. (3.15)
Применяя в (3.13) или в (3.15) формулу приведения, можно увидеть, что колебания потенциальной и кинетической энергии свершаются со сдвигом по фазе на p, поэтому полная механическая энергия системы не изменяется при гармонических колебаниях: сложив (3.12) и (3.14) получим
. (3.16)
Полная энергия остается постоянной вследствие закона сохранения механической энергии, поскольку упругая сила консервативна.
Потенциальная энергия пружинного маятника в произвольный момент времени согласно (3.14) и (3.9) равна
. (3.17)
Физическим маятником называется твердое тело произвольной формы, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, не проходящей через центр масс этого тела.
Записав для физического маятника основное уравнение динамики вращательного движения (уравнение моментов) и введя обозначение
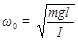, (3.18)
где m – масса тела; I – момент инерции физического маятника относительно оси подвеса; l – расстояние от оси подвеса до центра масс, можно получить для малых колебаний физического маятника уравнение
, (3.19)
идентичное с (3.6), решение которого (3.1*) известно:
, (3.20)
где a – угол отклонения маятника от вертикали; a 0 – амплитуда колебаний угла a.
Математический маятник можно рассматривать как предельный случай физического маятника, вся масса которого сосредоточена в его центре масс. Тогда формулы (3.19) и (3.20) относятся и к математическому маятнику. Момент инерции математического маятника
, (3.21)
где l – длина маятника. Подставляя (3.21) в (3.18), получим циклическую частоту малых колебаний математического маятника
(3.22)
и период колебаний
. (3.23)
Сравнивая формулы (3.6) для пружинного маятника и (3.19) для физического и математического маятников можно записать общее дифференциальное уравнение гармонических колебаний величины s в виде
, (3.24)
решением которого является функция (3.1*) или (3.1).
Затухающими колебаниями называются колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются. Рассмотрим свободные затухающие колебания пружинного маятника массы m, движущегося в вязкой среде вдоль оси x. На груз действуют две силы: сила упругости пружины и сила сопротивления среды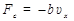 
, где b – коэффициент сопротивления (вязкого трения); ux – проекция скорости груза на ось x. По второму закону Ньютона, дифференциальное уравнение движения пружинного маятника в этом случае имеет вид
,
или
, (3.25)
где
, (3.26)
. (3.27)
Уравнение вида (3.25) получается и при рассмотрении других видов колебательных систем, в которых наблюдаются свободные затухающие колебания (например, колебательный контур). Поэтому можно утверждать, что общее дифференциальное уравнение свободных затухающих колебаний линейных[1] систем имеет вид:
, (3.28)
где s – колеблющаяся физическая величина; b =const³0 – коэффициент затухания; w 0 – циклическая частота свободных незатухающих колебаний той же системы, т.е. в отсутствие потерь энергии (при b =0).
Решением уравнения (3.28) в случае малых затуханий (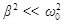
) является функция (рис. 3.2)
, (3.29)
где
(3.30)
– амплитуда затухающих колебаний; A 0 – начальная амплитуда;
(3.31)
– циклическая частота затухающих колебаний; w 0 – циклическая частота свободных незатухающих колебаний той же системы. Функция (3.29) может быть записана с синусом (вместо косинуса).
Для пружинного маятника функция (3.29) запишется в виде
. (3.32)
Эта функция – закон движения материальной точки, совершающей свободные затухающие колебания, – является решением дифференциального уравнения движения (затухающих колебаний) пружинного маятника (3.25).
Амплитуда затухающих колебаний уменьшается с течением времени тем быстрее, чем больше коэффициент затухания
Коэффициентом затухания 
называется величина обратная времени релаксации 
: 
.
Промежуток времени, в течение которого амплитуда затухающих колебаний уменьшается в е раз (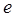
=2,718 - основание натурального логарифма), называется временем релаксации .
Логарифмическим декрементом затухания называется величина, характеризующая затухание колебаний системы за период Т, и равная логарифму отношения двух последующих амплитуд (т.е. в момент времени t и t+T):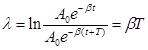 
.
За время релаксации система совершает 
колебаний. Подставив сюда 
и 
, получим: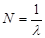 
. Следовательно: 
.
Т.е. 
- величина, обратная числу колебаний, совершаемых системой за время релаксации.
Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним не применимо понятие периода или частоты. Однако, если затухание мало, то можно условно пользоваться понятием периода, как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины (рис. 3.2). Тогда (условный) период затухающих колебаний с учетом формулы (3.31) равен
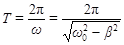. (3.33)
Для линейных систем этот период в процессе колебания остается постоянным.
Для характеристики быстроты убывания амплитуды затухающих колебаний пользуются величинами: декремент затухания и логарифмический декремент затухания. Для характеристики колебательной системы с точки зрения быстроты потерь энергии пользуются величиной добротность колебательной системы.
Рис. 3.2
Порядок выполнения работы Бригада №
1. В правом верхнем углу листа запишите № бригады(вариант).
2. Запустите программу. Выберите «Механика», «Механические колебания и волны» и «Свободные колебания» (сначала математический маятник, потом груз на пружине).
3.Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения.
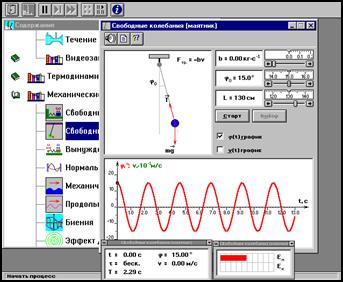
Модель. Свободные колебания (маятник)
Рис. 3.3