Лабораторная работа 4
РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ЛИНЕЙНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ВТОРОГО ПОРЯДКА МЕТОДОМ ПРОГОНКИ
Пусть на отрезке [ a,b ] требуется найти решение дифференциального уравнения
, (1)
удовлетворяющее следующим краевым условиям:
, 
, (2)
Численное решение задачи состоит в нахождении приближённых значений y 0, y 1, …, y n искомого решения y(x) в точках x 0, x 1, …, x n. Точки x 0, x 1, …, x n называются узлами сетки. Используем равномерную сетку, образованную системой равноотстоящих узлов 
i= 0, 1, 2, …, n. При этом x 0 =a, x n =b, h=(b-a)/n. Величина h – шаг сетки. Пусть p(xi)=pi, q(xi)=qi, f(xi)=fi, y(xi)=yi. Аппроксимируем y¢(xi) и y¢¢(xi) в каждом внутреннем узле центральными разностными производными
и на концах отрезка – односторонними производными
Используя эти формулы, получаем разностную аппроксимацию исходной задачи (1) – (2):
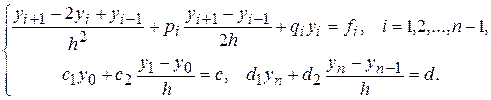(3)
Чтобы найти приближённые значения y 0, y 1, …, y n искомого решения, необходимо решить систему n +1 линейных уравнений (3) с n +1 неизвестными. Эту систему можно решить одним из стандартных методов решения линейных систем. Однако матрица системы (3) трёхдиагональная, поэтому для её решения применим специальный метод, называемый методом прогонки.
Перепишем систему (3) следующим образом:
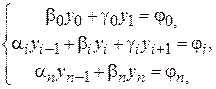
(4)
где b0= c 1 h – c 2, g0= c 2, j0= hc, j i = fih 2, a i =1–(1/2) pih, b i = qih 2–2, g i =1+(1/2) pih, i =1, 2, …, n –1, a n =– d 2, b n = hd 1+ d 2, j n = hd.
Будем искать решение системы (4) в виде
. (5)
тогда для ui и vi получаем следующие рекуррентные формулы:
.
Чтобы сделать схему счёта однородной, положим a0=0, gn=0. Прямой ход прогонки состоит в последовательном вычислении коэффициентов ui и vi, исходя из значений
v 0=–g0/b0, u 0=j0/b0.
При обратном ходе прогонки по формуле (5) последовательно определяются величины yn, yn-1, …, y 0. Так как gn=0, то vn =0 и yn = un, т.е. в прямом ходе прогонки вычисляются величины vn, un и приближённое значение решения yn на правом конце отрезка. Остальные величины yn-1, yn-2, …, y 0 вычисляются в обратном ходе прогонки по рекуррентной формуле (5). Таким образом, метод прогонки позволяет найти точное решение системы (3).
Погрешность решения краевой задачи (1)–(2) определяется только погрешностью разностной аппроксимации O (hk) исходной задачи системой (3). Порядок аппроксимации k равен 2, если с 2= d 2=0, или 1 в противном случае. Так как h =(b-a)/ n, то выбирая n достаточно большим, можно добиться уменьшения погрешности ценой увеличения объёма вычислений при решении системы (3).
При практической оценке погрешности найденного решения обычно используют правило Рунге. Если y (xi) – точное значение решения в узле xi, а yi и 
– приближённые значения решения в том же узле, полученные соответственно с шагом h и h /2, то оценка погрешности решения yi определяется формулой
, 
.
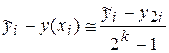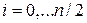Варианты заданий
На отрезке [ a, b ] решить методом прогонки линейную краевую задачу
Здесь 
| № | p(x) | Q(x) | a | b | c | d | a1 | a2 | b |
|
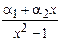
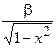
| 0,8 0,8 0,8 0,8 0,8 0,8 | -0,5 -0,375 | 0,5 0,1 -0,2 -0,4 -0,1 -0,3 | 1,4 1,8 | ||||
-2 x
|
| 0,5 0,5 0,5 | 0,8 0,8 0,8 0,6 0,6 0,6 0,6 0,6 0,6 0,6 0,8 0,8 0,8 0,8 0,8 0,8 0,8 0,8 | 0,2 0,15 -0,05 -0,1 -0,2 -0,5 0,4 -1 -1 -5 -0,5 -0,667 -0,625 | -0,5 -0,8 -1,3 0,8 0,2 0,2 -0,6 -1,2 -1,2 -0,9 0,896 -0,1264 -1,09824 -0,352 -0,843 -0,997 -0,7522 -0,2064 3,4 1,8 3,5 2,667 -1,292 | 2,2 2,6 1,5 1,7 1,9 2,1 2,3 2,5 2,3 | 2,5 2,7 2,9 3,1 3,3 3,5 2,7 | 33,5 34,5 35,5 36,5 37,5 33,5 |
ЛАБОРАТОРНАЯ РАБОТА 5
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА МЕТОДОМ СЕТОК
В настоящей лабораторной работе методом сеток требуется решить задачу Дирихле для уравнения Лапласа. Эта задача ставится следующим образом.
Найти непрерывную функцию и (х, у), удовлетворяющую внутри прямоугольной области 
уравнению Лапласа
и принимающую на границе области W заданные значения, т. е.
, 
,
, 
,
где f l, f 2, f 3, f 4 — заданные функции.
Будем считать, что и (х, у) непрерывна на границе области W, т. е. 
, 
, 
, 
. Выбрав шаги h, l по x и y соответственно, строим сетку 
, 
, 
, 
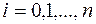, где 
, 
.
Вводя обозначения 
, аппроксимируем частные производные 
и 
в каждом внутреннем узле сетки центральными разностными производными второго порядка
,
и заменим уравнение Лапласа конечно-разностным уравнением
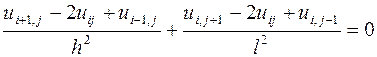, (1)
, 
.
Погрешность замены дифференциального уравнения разностным составляет величину 
.
Уравнения (1) вместе со значениями 
в граничных узлах образуют систему линейных алгебраических уравнений относительно приближенных значений функции и (х, у) в узлах сетки 
. Наиболее простой вид имеет эта система при 
:
(2)
, 
, 
, 
,
, .
При получении сеточных уравнений (2) была использована схема узлов, изображенная на рис. 22. Набор узлов, используемых для аппроксимации уравнения в точке, называется шаблоном. В данной работе используется шаблон типа «крест».
Численное решение задачи Дирихле для уравнения Лапласа в прямоугольнике состоит в нахождении приближенных значений искомой функции и (х, у) во внутренних узлах сетки. Для определения величин требуется решить систему линейных алгебраических уравнений (2).
В данной лабораторной работе она решается методом Гаусса—Зейделя, который состоит в построении последовательности итераций вида
(верхним индексом s обозначен номер итерации). При 
последовательность 
сходится к точному решению системы (2). В качестве условия окончания итерационного процесса можно принять
, 
, 
.
Таким образом, погрешность приближенного решения, полученного методом сеток, складывается из двух погрешностей: погрешности аппроксимации дифференциального уравнения разностными; погрешности, возникающей в результате приближенного решения системы разностных уравнений (2).
Известно, что описанная здесь разностная схема обладает свойством устойчивости и сходимости. Устойчивость схемы означает, что малые изменения в начальных данных приводят к малым изменениям решения разностной задачи. Только такие схемы имеет смысл применять в реальных вычислениях. Сходимость схемы означает, что при стремлении шага сетки к нулю (
) решение разностной задачи стремится в некотором смысле к решению исходной задачи. Таким образом, выбрав достаточно малый шаг h, можно как угодно точно решить исходную задачу.
Порядок выполнения работы на ПЭВМ
Составить подпрограммы решения задачи Дирихле, вычисления значений граничных функций 
, 
, 
, 
.
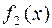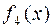Составить головную программу, содержащую обращения к подпрограммам, произвести вычисления.
Лабораторная работа № 6