Постановка задачи.
Пусть 
и заданы точки 
, 
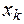(узлы интерполирования), в которых известны значения функции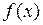 
. Задача интерполирования состоит в том, чтобы построить многочлен:
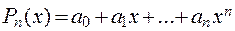
степени n, значения которого в заданных точках 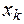, совпадают со значениями функции 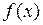в этих точках. Такой полином существует и единственен.
Интерполяционный многочлен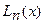 
степени не выше n по системе алгебраических многочленов 1, х, х²,…,xⁿ можно задать по формуле Лагранжа:
(☼) 
,где 
,
.
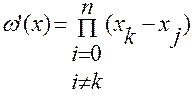Обозначая 
получим “барицентрический” вид многочлена Лагранжа:
Интерполяционная формула Ньютона.
Формула Ньютона является разностным аналогом формулы Тейлора и имеет вид: (1.1) 
где 
, i,j=0,1,…,n,
i≠j – разделенные разности первого порядка,
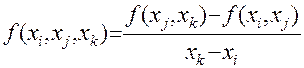, i,j,k=0,1,…,n,
i≠j≠k – разделенные разности второго порядка,
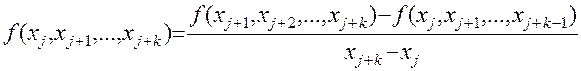– разделенные разности k -го порядка.
При выводе формулы Ньютона не накладывается ограничений на порядок узлов x0,x1,…,xn, поэтому множество интерполяционных формул можно получить из (1.1) перенумерацией узлов.
Погрешность интерполирования.
Заменяя функцию 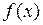интерполяционным многочленом 
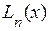, мы допускаем погрешность:
,
которая называется погрешностью интерполирования или остаточным членом интерполяционной формулы. Если функция 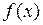имеет непрерывную (n+1)-ю производную, то имеет место следующая оценка остаточного члена:
(1.3)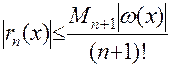 
,
где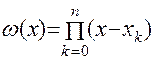 
, 
.
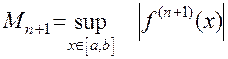Погрешность интерполирования можно представить также через разделенную разность следующим образом:
Минимизация остаточного члена интерполирования.
Из формулы (1.3) следует, что для данной функции 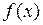погрешность интерполирования зависит от выбора узлов 
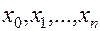на отрезке [a,b]. Величину 
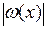можно минимизировать за счет выбора узлов интерполирования
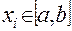, i=0,1,…,n.
Такими оптимальными узлами для отрезка [1,-1] являются корни многочлена Чебышева первого рода:
,
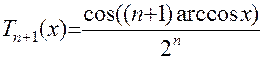которые вычисляются по формуле:
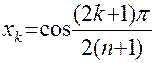, k=0,1,…,n.
В случае произвольного отрезка [a,b] из этого равенства получим формулу для оптимальных узлов:
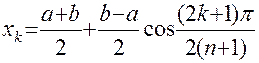, k=0,1,…,n.
При этом оценка (1.3) примет вид:
, и 
.
И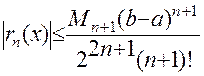нтерполирование по равноотстоящим узлам.
Приведем некоторые интерполяционные формулы для случая равноотстоящих узлов.
Пусть на отрезке [a,b] задана равномерная сетка 
, k=0,1,…,n и значения функции 
, h>0.
Пусть 
-- точка интерполирования. Тогда, используя (1.1), получаем первую интерполяционную формулу Ньютона:
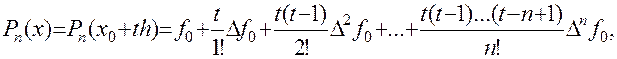
где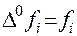 
, 
, i=0,1,…,k-n
конечные разности.
Положив 
, получаем вторую интерполяционную формулу Ньютона: 
Для двух последних интерполяционных формул оценка
погрешности интерполирования имеет вид:
,
.
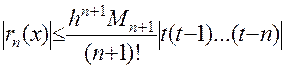При малых значениях h и при условии непрерывности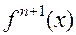 
можно приближенно считать:
, где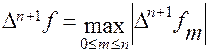 
.
Тогда оценка остаточных членов первой и второй интерполяционных формул Ньютона имеет вид:
(1.4) 
.
Формула (1.4) удобна тем, что позволяет делать оценку ошибки интерполирования без исследования (n+1)-й производной функции 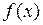. На окончательную погрешность интерполирования, разумеется, влияет и вычислительная погрешность, поэтому при вычислении интерполяционных многочленов желательно сводить число арифметических операций к минимуму.
6. Примеры:
1) Построить многочлен наименьшей степени, принимающий в данных точках следующие значения:
| Х | ||||
| У |
Вычислить в точке х=3 приближенное значение функции.
Решение: Воспользуемся формулой Лагранжа:
,
где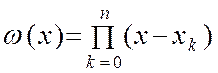 
,
, 
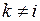получим:
2) С какой точностью можно вычислить по формуле Лагранжа
ln 100,5 по известным значениям ln 100, ln 101, ln 102, ln 103, ln 104?
Решение: Согласно формуле для остатка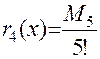 
.
Поскольку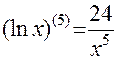 
, то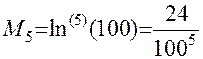 
,
Вычисляя:
w(x)=(100.5-100)(100.5-101)(100.5-102)(100.5-103)(100.5-104)=
=3.28125. Подставляя это в формулу для остатка, получаем:
.
Поэтому: 
3) Найти сумму конечного ряда нечетных чисел
S(p)=1+3+5+…+(2p-1)
Решение: Известно, что S(p) является некоторым многочленом относительно p. Применим интерполяционную формулу Ньютона. Составим таблицу разделенных разностей для S(p), а именно
,
,
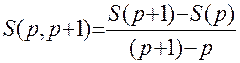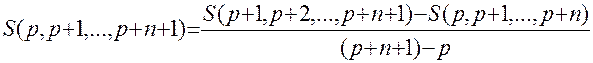
Таблицу составляем до тех пор, пока не получим разделенные разности, равные нулю.
| P | S(p) | S(p,p+1) | S(p,p+1,p+2) | S(p,p+1,p+2,p+3) |
| 1 | 3 | 1 | 0 |
Поскольку разделенные разности третьего порядка равны нулю,то S(p) является многочленом второй степени. Подставим подчеркнутые члены в формулу интерполяционного многочлена Ньютона, имеем:
S(p)=1+3(р-1)+1(р-1)(р-2)=р²
7. Контрольные задания:
Найти многочлен наименьшей степени, принимающий в данных точках заданные значения:
Вариант-1: Вариант-2: Вариант-3:
| X | Y | x | y | x | Y | ||
| 1,45 1,36 1,14 | 3,14 4,15 5,65 | 1,5 6,8 | 1,45 3,14 4,11 |
Дана таблица значений функции f(x):
| X | 2,0 | 2,3 | 2,5 | 3,0 | 3,5 | 3,8 | 4,0 |
| f(x) | 5,848 | 6,127 | 6,300 | 6,694 | 7,047 | 7,243 | 7,368 |
Пользуясь формулой Лагранжа, найти значения функции в указанных точках:
Вариант-4: 2,22;
Вариант-5: 2,41;
Вариант-6: 2,78;
Вариант-7: 3,34;
Вариант-8: 3,75;
Вариант-9: 3,88.
Используя “барицентрический” вид многочлена Лагранжа, найти значения функций, заданных таблицами, в указанных точках:
Вариант-10:
| X | ||||
| F(x) | 68,7 | 64,0 | 44,0 | 39,1 |
Найти f(20).
Вариант-11:
| X | 93,0 | 96,2 | 100,0 | 104,2 | 108,7 |
| f(x) | 11,38 | 12,80 | 14,70 | 17,07 | 19,91 |
Найти f(102).
Вариант-12:
| X | ||||||
| F(x) |
Найти f(5).
Построить интерполяционные многочлены Ньютона для функции
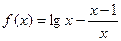по следующим узлам:
Вариант-13: х=1, 2, 4, 8, 10;
Вариант-14: х=2, 4, 8, 10;
Вариант-15: х=4, 8, 10;
Вариант-16: х=2, 4, 8.
(Для всех этих случаев вычислить приближенное значение lg5,25. Получить оценку погрешности остаточного члена.)
По данным таблицам значений функций определить значение аргумента х, соответствующее указанным значениям у, пользуясь многочленом Ньютона:
Вариант-17: у=0
| Х | 2,5 | |||
| У | -6 | -1 | 5,625 |
Вариант-18: y=20
| X | ||||
| Y |
Просуммировать конечные ряды:
Вариант-19: 1²+2²+3²+…+(n-1)²+n²;
Вариант-20: 1³+2³+3³+…+n³;
Вариант-21: 1²+3²+5²+…+(2n-1)²;
Вариант-22: 1³+3³+5³+…+(2n-1)³.
Дана таблица значений функции y=shx.
| X | Shx | x | Shx | |
| 1,0 1,1 1,2 1,3 1,4 | 1,17520 1,33565 1,50946 1,69838 1,90430 | 1,5 1,6 1,7 1,8 | 2,12928 2,37557 2,64563 2,94217 |
Найти приближенные значения shx для следующих значений аргумента:
Вариант-23: 1,01; 1,02; 1,03; 1,11; 1,12; 1,13;
(использовать первую интерполяционную формулу Ньютона)
Вариант-24: 1,75; 1,76; 1,78; 1,79.
(использовать вторую интерполяционную формулу Ньютона)