Для решения ряда практических задач необходимо знать закон распределения (или числовые характеристики) случайных величин вида Z = X ±Y, Z = X Y, Z = л/Х2 + У2, Z = max (я, У) и других.
Если каждой паре возможных значений с. в. X и У по определенному правилу соответствует одно возможное значение с. в. Z, то Z называют функцией двух случайных аргументов X и У, записывают Z = tp(X,Y).
Найдем закон распределения суммы двух случайных величин (наиболее важный на практике), т. е. закон распределения с. в. Z = X + У.
Пусть система двух непрерывных с. в. (X, У) имеет совместную плотность распределения f(x, у). Найдем по формуле (3.8) функцию распределения с. в. Z = X + У.
Fz(z) = P{Z<z} = P{X + Y<z} = ff ffay)dxdy.
Dz
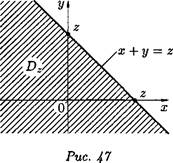
Здесь Dz — множество точек плоскости Оху, координаты которых удовлетворяют неравенству х + у < г, см. рис. 47.
 оо z—x
оо z—x
|
Имеем
Fz(г)г= /(/ ffav^v)**-
—оо —оо
Дифференцируя полученное равенство по переменной г, входящей в верхний предел внутреннего интеграла, получаем выражение для плотности распределения с. в. Z = X + У:
fz(z)= J f{x,z-x)dx. (4.6)
-оо
Если с. в. X и У независимы, то, как известно (п. 3.4), f(x,у) = — fl(x)f2(y)- Формула (4.6) примет вид
оо
fz(z) = fx+Y(z)= j h(x)f2(z-x)dx. (4.7)
—оо
Закон распределения суммы независимых с. в. называется композицией или сверткой законов распределения слагаемых.
Плотность распределения с. в. Z можно записать в виде fx+y ~ = fx * /у> где * — знак свертки, а формулу (4.7) называют формулой свертки или формулой композиции двух распределений.
Записав Z в виде Z = У+Х, можно получить другое представление для fziz)y а именно
оо
fz{z) = J f(z~y,v)dy
—оо
и
оо
fz{z)= J fi(z-y)f2(y)dy
—оо
в случае независимости с. в. X и У.
Задача нахождения закона распределения с. в, вида Z = X — У, Z = X ' У и других решаются аналогично.
Пример 4.4. Пусть с. в. X ~ iV(0,1), с. в. У ~ JV(0,1). Найти закон распределения с. в. Z — X + У, считая X и У независимыми с. в.
О Используя формулу (4.7), получаем
ОО Л,, 9 оо „
| / |
1 1 (2 - х) Л Г 2х2 - 2гх + z2
—оо -оо
ОО §)2 + т) 2 00 ч2
к!е------ s = кеЛ / е~И) d (*-1) =
2тг
—oo —oo
Ч/2\/2тг
/. N
/ e u du~ \fn — интеграл Пуассона
т. е.
Сумма независимых нормальных с. в. (с т — 0, а = 1) имеет нормальное распределение (с т = 0, с = \/2). •
Пример 4.5. Совместное распределение с. в. X и Y задано плотностью распределения вероятностей
Я*,!/) = {о,
Найти плотность распределения вероятностей с. в. Z — X — Y.
О Найдем сначала функцию распределения F(z) с. в. Z, а затем — ее производную F'z(z) - fz(z).
Fz(z) = P{Z <z} = P{X - Y < z) = fJiz + У) dxdyt
где Dz — множество точек, координаты которых удовлетворяют неравенству х — у < 2, т. е. у > x — z (они находятся выше прямой у — х — z), где z — произвольное число. Очевидно, если г ^ —1, то F(z) — 0; так как f{x,y) = 0 вне квадрата Область интегриро
|
| x — z |
| х—г |
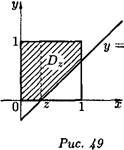
вания Dz при —1 < 2 < 0 изображена на рис. 48, при 0 < г ^ 1 — на рис. 49).

|
| у = х — Z |
| Рис. 48 При — 1 < z ^ 0 имеем |
ltz 1 ^
F{z) = JJ{x + у) dxdy = j dx J {x +у) dy= J dx ^xy +
Ds 0 x-z 0
1+z
= J (X + ±-X2+xz~ (X~2Z^ ^jdx = 0
(x2. 1Д x3|2,x2 - \ 2 + 2 3 2 6 J 0 "
| + г/, при O^z^l, 0 < у ^ 1, в противном случае. |
_ (1 -Yz)2, 1 + z (1 + 2)3, z(\ + z)2 x гз ^ (3, + iy
При 0 < z ^ 1 имеем
z 1 11
F{z) = JJ (х + у) dxdy = J dx J{x + y)dy + J dx J (x + y)dy =
Dz 0 0 z x—z
-f i+idx(xy+Y) l =
0 z
z 1
= J (x + i) dx + J ^x + | - x2 + xz - ^ ^ da; =
о г
/х2 x\ г, fx2, x x3. „х2 11
^ 2 2y o \2 2 3 2 6
_ г2, z, 1 г2, 1 z LzV z3 U^*)3 п=-г2 + 2г + 1
"г^г^г 2~^2 2 3 3^2 26 2
При z > 1 имеем
l l
= JJ(X + y) dxdy = J dx J{x + y)dy =
D, 0 0
| = 1. |
Ж, X 2 2
Таким образом,
при z ^ — 1, при — 1 < г ^ 0,
| fo, (z + l)2 |
| Fz(z) = |
| -г2 + 2z + 1 1. |
, при 0 < z < 1, при 2 > 1.
| Следовательно, Контроль: |
О, при z ^ —1, z > 1, = /2(2) = ^ + 1, при - 1 < г ^ 0, 1 — z, при 0 < z ^ 1.
-1
J f(z) dz — J 0 dz + J [z + \)dz + J (l-z)dz + J 0 dz
-l о 1
(z + l)2 0 (1 ~z)2 1
= i-0-0+i = l. О 2 z
IsT] Пример 4.6. Независимые с. в. X и У распределены равномерно X ~ Л[0,4], У ~ Л[0,1]. Найти плотность распределения вероятностей с. в. Z = X + Y (рис. 50).
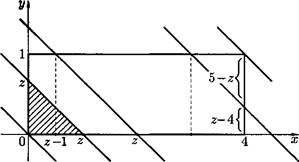 x+y — z x+y — z Рис. 50
x+y — z x+y — z Рис. 50
|
| x+y = z |
Q Система с. в. (X, У) равномерно распределена в прямоугольнике /l(X) \0| s*[0,4], Ш) (О, у* [0,1].
Так как с. в. X и У независимы, то /(ж,у) = f\(x) • fi(y) = ^ - 1 —
Fz(z)=P{X + Y <z}= JJ \dxdy = \sDz,
Dz
(x+y<z)
где Sdz — площадь области Dz — части прямоугольника, лежащей ниже прямой х + у = z. Если z < 0, то F(z) = 0; если 0 < г < 1, то F(z) = ^ ■ JjZ2 (так как Sdz = ^ * г • z); если 1 < z ^ 4, то
F(z) = \ ■ • l) = - 1);
если 4 < 2г < 5, то
F(z) = i • (l • 4 - 1(5 - *)(S - z)) = |(8 - (5 - zf).
Итак,
| Го, Ь 1 4' |
| f(z) = F'z{z) = |
z < 0, 2 > 5, 0 < г < 1,
1 < * < 4, -z), 4<z^5.
Контроль:
oo
j f{z)dz = J \zdz + f\dz + ± J (5 — z)dz = 1.
-oo 0 14
Плотность распределения fz{z) можно найти, используя формулу
оо
/М = J f\{x)-f2{z-x)dx.
—оо
4 4
/(*) = J \f2(z-x)dx^± J f2(z-x)dx.
о 0
Функция под знаком интеграла отлична от нуля лишь в случае
Г 0 < х < 4, \0 ^ z — ж ^ 1,
— 1 < яг z.
Решение системы зависит от значения z.
1. Если 2^0, система несовместна; отрезки [0,4] и [z — l,z] не пересекаются, (см. рис. 51).
Следовательно, f2(z — ж) = 0 и fx+y{z) = 0.
| Имеем |
| т.е. |
| (4.8) |
2. Если 0 < z ^ 1, система (4.8) эквивалентна неравенству 0 ^ х < z (см. рис. 52).
-- K/WVyj
z—1 z
О 4 х
Рис. 51
М////Л
z—1 Z
О 1 4
Рис. 52
Поэтому
z
| -_ z_ £ " 4Х\о~ 4- |
fx+y{z) = \ Jldx = \
3. Если 1 < г ^ 4, система (4.8) эквивалентна неравенству z — 1 < ^ х < г (см. рис. 53).
Vf'/t'/zi
z—\ z
О 1 А
Рис. 53
Поэтому
z
fx+Y(*) = \ j ldz=\x\'z_=±(z-z + l) = \. 2-1
4. Если 4 < г < 5, toz~1^o;<4 (см. рис. 54).
----------------- ЮООООЧ—(-
z—1 z 5
Рис. 54
Поэтому
| 5~z 4 ' |
fz(z) = \ I Uz = ±z|V= 1(4 -г 4-1) =
z-1
| /(*) = |
Рис. 55
5. Если 5 < г, то система (4.8) несовместна (см. рис. 55), а, значит, fz{z) = 0. Итак,
| ГО, | |
| h | |
| 4' | |
| 1 < г ^ 4, |
Упражнения
1. По условию примера 4.5 найти функцию и плотность распределения вероятностей с. в. Z = X + Y.
2. По условию примера 4.5 найти плотность распределения вероятно-
у
стей с. в. Z = -гр.