Лучшее соответствие экспериментальным данным показала функция вида
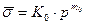 , (1)
, (1)
где  ,
,  – «коэффициент прочности» и показатель упрочнения, постоянные материала в данных условиях;
– «коэффициент прочности» и показатель упрочнения, постоянные материала в данных условиях;
 – логарифмическая пластическая деформирования;
– логарифмическая пластическая деформирования;
 – действительное напряжение;
– действительное напряжение;
 – условное напряжение, определяемое отношением силы, приложенной к образцу, к начальной площади поперечного сечения;
– условное напряжение, определяемое отношением силы, приложенной к образцу, к начальной площади поперечного сечения;
 – пластическая деформация в направлении приложения нагрузки при одноосном растяжении.
– пластическая деформация в направлении приложения нагрузки при одноосном растяжении.
Для пластичного материала (таблица 1)
 ,
,
поэтому значение показателя упрочнения вычисляется по формуле
 .
.
При известном показателе m 0 коэффициент прочности K 0 определяется с помощью выражения [2]
 .
.
Зависимость, аппроксимирующая кривую статического деформирования, имеет вид
 . (2)
. (2)
 Кривая статического деформирования представлена в графической (рисунок 2) и табличной (таблица 9) формах.
Кривая статического деформирования представлена в графической (рисунок 2) и табличной (таблица 9) формах.
Используя степенной закон упрочнения вида (1) для описания диаграммы деформирования, можно определить истинное сопротивление разрыву
 ,
,
где 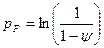 ресурс пластичности материала.
ресурс пластичности материала.
Подставляя данные из таблицы 1, определим
 ;
;
 .
.
Таблица 9. Зависимость истинного напряжения от логарифмической
пластической деформации при статическом растяжении
| p, % | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | |
 , МПа , МПа
|

 Рисунок 2. Кривая статического деформирования
Рисунок 2. Кривая статического деформирования
сплава ХН73МБТ (ЭИ698)
 3.2 Определение параметров циклической кривой в симметричном цикле
3.2 Определение параметров циклической кривой в симметричном цикле
Результаты упругих циклических испытаний представляются в виде кривых малоцикловой усталости, описываемых
 – уравнением Дж. Морроу;
– уравнением Дж. Морроу;
 – уравнением Мэнсона-Коффина,
– уравнением Мэнсона-Коффина,
где 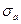 – амплитуда напряжения в цикле;
– амплитуда напряжения в цикле;
 – амплитуда пластической деформации в цикле;
– амплитуда пластической деформации в цикле;
 – долговечность – число циклов до разрушения;
– долговечность – число циклов до разрушения;
B, β, C, α – константы материала.
Постоянные B, β, C, α этих уравнений определяют по результатам испытаний большого числа (не менее 10) образцов, используя при обработке данных метод “наименьших квадратов”.
Кривые усталости могут быть представлены в форме уравнения Мэнсона-Лэнджера
 . (3)
. (3)
По кривым усталости получают циклическую кривую – зависимость  для стабилизированного состояния материала. Обработка широкого массива экспериментальных данных позволила установить, что и циклическую кривую можно аппроксимировать степенной зависимостью
для стабилизированного состояния материала. Обработка широкого массива экспериментальных данных позволила установить, что и циклическую кривую можно аппроксимировать степенной зависимостью
 , (4)
, (4)
где  ,
, 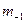 – постоянные материал.
– постоянные материал.
Для определения констант  ,
, 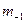 при известных параметрах кривой усталости необходимо выразить из уравнения Мэнсона-Коффина величину
при известных параметрах кривой усталости необходимо выразить из уравнения Мэнсона-Коффина величину  и подставить ее в уравнение Морроу:
и подставить ее в уравнение Морроу:
 ;
;

 .
.
Подставим данные из таблицы 1 и получим
 ;
;
 .
.
Уравнение циклической кривой деформирования в симметричном цикле для сплава ХН73МБТ (ЭИ 698) имеет вид
 . (5)
. (5)
Предел пропорциональности при циклическом нагружении  можно определить по формуле
можно определить по формуле
 . (6)
. (6)
Предел пропорциональности при симметричном цикле
 .
.
Циклическая кривая в симметричном цикле представлена в графической (рисунок 3) и табличной (таблица 10) формах.
Таблица 10. Зависимость амплитуды напряжения от амплитуды
пластической деформации в симметричном цикле
| p, % | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | |
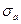 , МПа , МПа
|

 Рисунок 3. Циклическая кривая в симметричном цикле
Рисунок 3. Циклическая кривая в симметричном цикле
 3.3 Определение параметров циклической кривой в пульсационном цикле
3.3 Определение параметров циклической кривой в пульсационном цикле
При несимметричном «жестком» нагружении цикл напряжений за счет циклической релаксации напряжений стремится к симметричному. Особенно значительным квазистатическое повреждение может оказаться в условиях «мягкого» несимметричного нагружения, если амплитуда 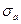 достаточно велика, сопоставима с переделом прочности
достаточно велика, сопоставима с переделом прочности  , то может происходить одностороннее накопление деформации
, то может происходить одностороннее накопление деформации  , которое вносит дополнительное статическое повреждение.
, которое вносит дополнительное статическое повреждение.
При малых величинах 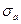 статическое повреждение незначительно, его можно не учитывать. В этом случае параметры уравнения Мэнсона-Коффина довольно слабо зависят от коэффициента асимметрии
статическое повреждение незначительно, его можно не учитывать. В этом случае параметры уравнения Мэнсона-Коффина довольно слабо зависят от коэффициента асимметрии  , тогда как для параметров уравнения Морроу (
, тогда как для параметров уравнения Морроу ( ) такая зависимость оказывается существенной. Это параметры можно определить с помощью диаграммы предельных амплитуд (диаграммы Хея). Получение полной диаграммы предельных амплитуд для ряда значений долговечности и тысячи марок конструкционных материалов представляют весьма трудоемкую задачу. В связи с этим используют линейную аппроксимацию диаграммы предельных амплитуд (аппроксимацию по Кинасошвили), которая представлена на рисунке 3. Ошибка аппроксимации диаграммы Хея идет всегда в запас.
) такая зависимость оказывается существенной. Это параметры можно определить с помощью диаграммы предельных амплитуд (диаграммы Хея). Получение полной диаграммы предельных амплитуд для ряда значений долговечности и тысячи марок конструкционных материалов представляют весьма трудоемкую задачу. В связи с этим используют линейную аппроксимацию диаграммы предельных амплитуд (аппроксимацию по Кинасошвили), которая представлена на рисунке 3. Ошибка аппроксимации диаграммы Хея идет всегда в запас.

Рисунок 4. Линейная аппроксимация диаграммы Хея
 На рисунке использованы следующие обозначения:
На рисунке использованы следующие обозначения:
 – определяет угол наклона луча подобных циклов, для которых
– определяет угол наклона луча подобных циклов, для которых  ;
;
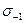 – предел усталости (предельная амплитуда) в симметричном цикле;
– предел усталости (предельная амплитуда) в симметричном цикле;
 – предельное (соответствующее разрушению) истинное напряжение при однократном монотонном растяжении;
– предельное (соответствующее разрушению) истинное напряжение при однократном монотонном растяжении;
 – предельная амплитуда в несимметричном цикле;
– предельная амплитуда в несимметричном цикле;
 – предельное среднее напряжение в несимметричном цикле;
– предельное среднее напряжение в несимметричном цикле;
 – величина, определяющая наклон аппроксимирующей диаграмму предельных амплитуд прямой.
– величина, определяющая наклон аппроксимирующей диаграмму предельных амплитуд прямой.
Диаграмма Хея позволяет определить предельные для данной долговечности амплитуду цикла с коэффициентом асимметрии 

и соответствующее среднее напряжение  .
.
Для пульсационного цикла ( ),
),  , получаем
, получаем

( – предел усталости в пульсационном цикле).
– предел усталости в пульсационном цикле).
Тогда уравнения кривых усталости для пульсационного цикла можно записать в виде
 (7)
(7)
где B, β, C, α – константы кривых усталости в симметричном цикле;
BR=0, βR=0 – константы кривых усталости в пульсационном цикле.
 Задавшись двумя значениями долговечности
Задавшись двумя значениями долговечности  (например,
(например,  ,
,  ), и зная константы материала B, β, C, α (таблица 1), определяем коэффициенты BR=0, βR=0 из уравнения (7)
), и зная константы материала B, β, C, α (таблица 1), определяем коэффициенты BR=0, βR=0 из уравнения (7)  :
:
 ,
, 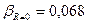 .
.
Затем находим параметры циклической кривой для пульсационного цикла
 ;
;
 .
.
Получаем уравнение циклической кривой деформирования в пульсационном цикле для сплава ХН73МБТ (ЭИ698)
 . (8)
. (8)
Определим предел пропорциональности в пульсационном цикле из уравнения (6)
 .
.
Циклическая кривая в пульсационном цикле представлена в графической (рисунок 4) и табличной (таблица 11) формах.
Таблица 11. Зависимость амплитуды напряжения от амплитуды
пластической деформации в пульсационном цикле
| p, % | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | |
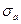 , МПа , МПа
|
 Циклическая кривая для симметричного цикла проходят выше кривой статического деформирования в диапазоне пластических деформаций
Циклическая кривая для симметричного цикла проходят выше кривой статического деформирования в диапазоне пластических деформаций  , что соответствует циклическому упрочнению материала на этом диапазоне деформирования (рисунок 5). Циклическая кривая для пульсационного цикла проходит ниже кривой статического деформирования, что соответствует циклическое разупрочнение на всем диапазоне деформирования.
, что соответствует циклическому упрочнению материала на этом диапазоне деформирования (рисунок 5). Циклическая кривая для пульсационного цикла проходит ниже кривой статического деформирования, что соответствует циклическое разупрочнение на всем диапазоне деформирования.

1 – кривая статического деформирования;
2 – циклическая кривая в симметричном цикле;
3 – циклическая кривая в пульсационном цикле;
Рисунок 5. Сопоставление кривой статического деформирования с циклическими кривыми
При малых амплитудах пластической деформации ( ) отношение амплитуды напряжений для циклической кривой в симметричном цикле к напряжению при статическом деформировании (степень циклического упрочнения материала в симметричном цикле) равна δ = 1,186, степень циклического упрочнения для пульсационного цикла равна δ = = 0,729. При больших амплитудах пластической деформации (
) отношение амплитуды напряжений для циклической кривой в симметричном цикле к напряжению при статическом деформировании (степень циклического упрочнения материала в симметричном цикле) равна δ = 1,186, степень циклического упрочнения для пульсационного цикла равна δ = = 0,729. При больших амплитудах пластической деформации ( ) степень циклического упрочнения материала для циклической кривой в симметричном цикле δ = 1,327, для пульсационного цикла степень циклического упрочнения равна δ = 0,737.
) степень циклического упрочнения материала для циклической кривой в симметричном цикле δ = 1,327, для пульсационного цикла степень циклического упрочнения равна δ = 0,737.
По рисунку 5 можно увидеть, что в процессе циклического нагружения данный материал в симметричном цикле при малых амплитудах деформации 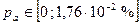 разупрочняется. При больших амплитудах пластической деформации материал упрочняется без стабилизации (
разупрочняется. При больших амплитудах пластической деформации материал упрочняется без стабилизации ( ) в симметричном цикле. В пульсационном цикле материал циклически разупрочняется на всем диапазоне деформирования
) в симметричном цикле. В пульсационном цикле материал циклически разупрочняется на всем диапазоне деформирования  .
.

4 ОПРЕДЕЛЕНИЕ МАКСИМАЛЬНОГО НАПРЯЖЕНИЯ ПО КРИТЕРИЯМ СТАТИЧЕСКОЙ ПРОЧНОСТИ
 |
В основу Норм расчетов на прочность атомных энергетических установок [1] положены расчетные оценки по следующим предельным состояниям:
1) кратковременное разрушение (вязкое и хрупкое);
2) разрушение в условиях ползучести при статическом нагружении;
3) пластическое течение по всему сечению детали;
4) накопление деформации ползучести;
5) циклическое накопление неупругой деформации, которое приводит к формоизменению детали;
6) возникновение макротрещин при циклическом нагружении;
7) потеря устойчивости сжатых элементов.
При проведении проверочного расчета действующие напряжения делят на категории:
 – общие мембранные напряжения – средние напряжения по поперечному сечению;
– общие мембранные напряжения – средние напряжения по поперечному сечению;
 – местные мембранные напряжения (средние напряжения в зонах краевых эффектов);
– местные мембранные напряжения (средние напряжения в зонах краевых эффектов);
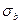 – общие изгибные напряжения, вызванные силовыми воздействиями;
– общие изгибные напряжения, вызванные силовыми воздействиями;
 – местные изгибные напряжения;
– местные изгибные напряжения;
 – температурные напряжения;
– температурные напряжения;
 – местные температурные напряжения;
– местные температурные напряжения;
 – напряжения компенсации (кинематическое воздействие) и др.
– напряжения компенсации (кинематическое воздействие) и др.
 Расчет по критерию статической прочности проводят для следующих расчетных случаев:
Расчет по критерию статической прочности проводят для следующих расчетных случаев:
1) НУЭ – нормальные условия эксплуатации:
 ,
,  ;
;
2) ННУЭ – нарушение нормальных условий эксплуатации:
 ,
,  ;
;
3) АС – аварийные ситуации:
 ,
,  .
.
Основное допускаемое напряжение  определяют из условия
определяют из условия
 , (9)
, (9)
здесь  – минимальное значение предела прочности
– минимальное значение предела прочности  при расчетной температуре;
при расчетной температуре;
 – минимальное значение предела текучести
– минимальное значение предела текучести 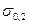 при расчетной температуре;
при расчетной температуре;
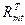 – минимальное значение предела длительной прочности, соответствующее расчетному ресурсу конструкции при расчетной температуре.
– минимальное значение предела длительной прочности, соответствующее расчетному ресурсу конструкции при расчетной температуре.
Минимальные значения расчетных сопротивлений 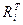 определяют по средним значениям этих величин и коэффициентами вариации в предположении, что распределение значений механических характеристик подчиняется нормальному закону.
определяют по средним значениям этих величин и коэффициентами вариации в предположении, что распределение значений механических характеристик подчиняется нормальному закону.
Анализируя данные литературы, можно сделать вывод, что для конструкционных сталей и сплавов можно принять следующие средние значения коэффициентов вариации:
 ;
;  ,
,
 где
где 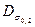 – среднеквадратичное отклонение предела текучести
– среднеквадратичное отклонение предела текучести 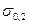 ;
;
 – математическое ожидание
– математическое ожидание 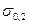 ;
;
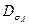 – среднеквадратичное отклонение предела прочности
– среднеквадратичное отклонение предела прочности  ;
;
 – математическое ожидание
– математическое ожидание  .
.
Поскольку сплав ХН73МБТ (ЭИ698) при заданной температуре существенной ползучести не проявляется, длительная прочность в этих условиях не является предельным состоянием. Следовательно, в дальнейшем предел длительной прочности 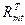 не принимается во внимание.
не принимается во внимание.
Для нормального закона распределения минимальное значение величины  с вероятностью 0,997 будет равно
с вероятностью 0,997 будет равно
 .
.
При указанных значениях коэффициентов вариации получим
 (10)
(10)
что позволяет определить величину допускаемого напряжения  .
.
При оценке статической прочности конструктивных элементов в нормальных условиях эксплуатации условие прочности согласно Нормам имеет вид
 ;
;  , (11)
, (11)
где  – среднее по поперечному сечению напряжение, связанное с нормальной силой N;
– среднее по поперечному сечению напряжение, связанное с нормальной силой N;

 – максимальное напряжение изгиба, определяемое изгибающим моментом M;
– максимальное напряжение изгиба, определяемое изгибающим моментом M;
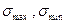 – наибольшее и наименьшее (с учетом знака) напряжения в опасном сечении.
– наибольшее и наименьшее (с учетом знака) напряжения в опасном сечении.
Для определения допускаемого напряжения воспользуемся заданными механическими характеристиками сплава ХН73МБТ (ЭИ698) (таблица 1). По формулам (10) определим  и
и  :
:
 ;
;
 .
.
Из условия прочности (9) определим допускаемое напряжение
 .
.
Мембранные и изгибные напряжения определяются по следующим формулам:
 ;
;  .
.
Учитывая, что  (таблица 2), определим среднее по поперечному сечению напряжение и максимальное напряжение изгиба
(таблица 2), определим среднее по поперечному сечению напряжение и максимальное напряжение изгиба
 (12)
(12)

 ;
;  .
.

 Рисунок 6. Эпюры распределения напряжения по высоте номинального сечения AB в плоском стержне с галтельным переходом между участками от нормальной силы
Рисунок 6. Эпюры распределения напряжения по высоте номинального сечения AB в плоском стержне с галтельным переходом между участками от нормальной силы  , изгибающего момента
, изгибающего момента  и суммарного воздействия
и суммарного воздействия 
Подставим в условия прочности (11) найденные категории напряжений (12)

Определим предельную величину максимального напряжения 
 . (13)
. (13)
 При нагружении одновременно нормальной силой N и изгибающим моментом M данного элемента конструкции (рисунок 6) из Норм расчетов на прочность (11) нормальные напряжения достигают максимального значения в точке A (
При нагружении одновременно нормальной силой N и изгибающим моментом M данного элемента конструкции (рисунок 6) из Норм расчетов на прочность (11) нормальные напряжения достигают максимального значения в точке A ( ). Напряжения в точке B равны
). Напряжения в точке B равны  .
.
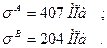 (14)
(14)
 5 ОПРЕДЕЛЕНИЕ ТЕОРЕТИЧЕСКОГО КОЭФФИЦИЕНТА КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ
5 ОПРЕДЕЛЕНИЕ ТЕОРЕТИЧЕСКОГО КОЭФФИЦИЕНТА КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ
Одним из основных факторов, который необходимо учитывать при расчетах на циклическую прочность, является концентрация напряжений. Реальная деталь отличается от своей расчетной схемы и образцов наличием различных геометрических и механических особенностей, которые могут вызвать местное (локальное) увеличение напряжений. Многочисленные экспериментальные и теоретические исследования показали, что в области механических или геометрических неоднородностей элемента конструкции возникает местное (локальное) увеличение напряжений. Такая особенность распределения напряжений получила название концентрации напряжений.
Основным показателем местных напряжений является теоретический коэффициент концентрации напряжений (при изгибе, растяжении-сжатии, кручении)
 , (15)
, (15)
где  – наибольшее местное напряжение;
– наибольшее местное напряжение;
 – номинальные напряжения, определенные без учета концентрации.
– номинальные напряжения, определенные без учета концентрации.
Теоретический коэффициент концентрации определяется для идеально упругого тела. Он не описывает полностью характер изменения местных напряжений, а характеризует только относительное увеличение одной наибольшей компоненты напряженного состояния.
Величина теоретического коэффициента концентрации определена для основных, часто встречающихся на практике типовых элементов конструкции. Данные по величине  приводятся в виде таблиц и графиков в справочной литературе.
приводятся в виде таблиц и графиков в справочной литературе.
Таблица 12. Значения теоретического коэффициента концентрации
напряжений для плоского стержня с галтельным переходом между участками при испытании на изгиб
| |||||||

| 0,02 | 0,05 | 0,10 | 0,15 | 0,20 | 0,25 | 0,30 |
| 6,0 | 3,26 | 2,66 | 2,05 | 1,75 | 1,55 | 1,47 | 1,40 |
| 2,0 | 3,0 | 2,35 | 1,85 | 1,65 | 1,50 | 1,43 | 1,35 |
| 1,2 | 2,70 | 2,08 | 1,70 | 1,54 | 1,47 | 1,35 | 1,32 |
| 1,05 | 2,30 | 1,84 | 1,57 | 1,46 | 1,37 | 1,32 | 1,30 |
Таблица 13. Значения теоретического коэффициента концентрации
напряжений для плоского стержня с галтельным
 переходом между участками при испытании на
переходом между участками при испытании на
растяжение
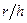
| |||||||

| 0,02 | 0,05 | 0,10 | 0,15 | 0,20 | 0,25 | 0,30 |
 ≥ 2 ≥ 2
| 5,25 | 3,0 | 2,3 | 2,0 | 1,85 | 1,70 | 1,65 |
| 1,50 | 4,20 | 2,72 | 2,15 | 1,86 | 1,73 | 1,63 | 1,57 |
| 1,15 | 3,20 | 2,15 | 1,70 | 1,56 | 1,45 | 1,30 | 1,28 |
| 1,05 | 2,35 | 1,74 | 1,48 | 1,40 | 1,33 | 1,12 | 1,11 |
Для элемента конструкции (рисунок 1) используя линейную интерполяцию значений теоретических коэффициентов концентрации (таблицы 12, 13), определим теоретические коэффициенты концентрации напряжений при заданных соотношениях  ,
,  (таблица 2) при растяжении и изгибе
(таблица 2) при растяжении и изгибе
 (16)
(16)
 Общий коэффициент концентрации напряжений в опасной точке A для плоского стержня с галтельным переходом между участками, находящегося в условиях одновременного растяжения и изгиба (рисунок 1), можно представить следующим образом:
Общий коэффициент концентрации напряжений в опасной точке A для плоского стержня с галтельным переходом между участками, находящегося в условиях одновременного растяжения и изгиба (рисунок 1), можно представить следующим образом:
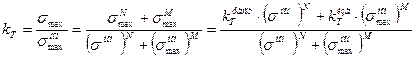 , (17)
, (17)
где  – максимальное номинальное напряжение в зоне концентрации при изгибе (без учета концентрации напряжений);
– максимальное номинальное напряжение в зоне концентрации при изгибе (без учета концентрации напряжений);
 – номинальное напряжение в зоне концентрации при растяжении (без учета концентрации напряжений);
– номинальное напряжение в зоне концентрации при растяжении (без учета концентрации напряжений);
 ,
,  – теоретические коэффициенты концентрации напряжении при изгибе и растяжении;
– теоретические коэффициенты концентрации напряжении при изгибе и растяжении;
Определим номинальные напряжения при растяжении  и максимальные номинальные напряжения при изгибе
и максимальные номинальные напряжения при изгибе  из формул (12) и (14), которые изображены на рисунке 6
из формул (12) и (14), которые изображены на рисунке 6
 (18)
(18)
Подставляя максимальные номинальные напряжения при растяжении и изгибе (18) и теоретические коэффициенты концентрации (16) в выражение (17), получим
 . (19)
. (19)