Кафедра математики и естественнонаучных дисциплин
Борисова О.Н.
Интегральное исчисление функций одной переменной
Сборник контрольных задач и методических указаний
Королев, 2009
Борисова О.Н. Интегральное исчисление функций одной переменной. Сборник контрольных задач и методических указаний. - Королев: КИУЭС, 2009, 54 с.
Рецензенты: к.п.н., доцент Федосеева З.Р.
Сборник включает в себя задачи контрольных работ по курсу «Математика», раздел интегральное исчисление, и методических указаний по их решению. Предназначен для проведения практических занятий, контрольных работ, а также для самостоятельной работы студентов всех специальностей, изучающих данный курс.
| РЕКОМЕНДОВАНО Учебно-методическим советом КИУЭС Протокол № от 2009 г. | Учебное пособие рассмотрено и одобрено на заседании кафедры математики. Протокол № от 2009 г. |
| Зав. кафедрой математики и естественнонаучных дисциплин КИУЭС д.ф.-м.н., профессор Борисов В.Ф. |
Введение
Данное пособие содержит подборки задач, предназначенных как для самостоятельного решения, так и для проведения контрольных работ по курсу «Интегральное исчисление функций одного вещественного переменного». Все разделы содержат краткие формулировки основных понятий и теорем, необходимых для решения задач. В сборник включено 3 контрольные работы, каждая из которых приводится в 25 различных вариантах. Каждой контрольной работе предшествует разбор типового варианта.
Неопределённый интеграл
Первообразной от непрерывной функции f (x) называется любая функция F (x), для которой выполнено соотношение
.
Для любой функции f (x) имеется много первообразных, однако все они отличаются друг от друга на константу: если F 1(x) и F 2(x) – первообразные от f (x), то 
.
Совокупность всех первообразных называется неопределенным интегралом от f (x) и обозначается так:
.
Здесь F (x) − любая фиксированная первообразная. Прямым дифференцированием можно проверить справедливость следующих соотношений.
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
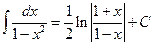
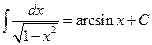
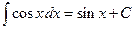
Частные случаи формулы 
:
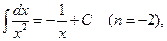
Имеется два основных приема вычисления неопределенных интегралов.
Замена переменной
Это наиболее часто используемый прием.
.
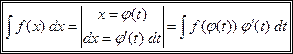Интегрирование по частям
Интегрирование по частям позволяет «перебросить» производную с одного множителя, входящему в интегрируемую функцию, на другой
Во многих случаях угадать формулу замены переменной, упрощающей интегрируемую функцию, помогает занесение множителя под знак дифференциала
,
где 
− произвольная первообразная функции 
.
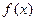Так как производная постоянной функции равна нулю, а постоянный множитель можно выносить за знак дифференциала, для произвольных постоянных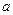 
и 
имеет место формула
.
Рекомендуется запомнить следующие формулы
| 
|
| 
|
| 
|
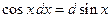
Разберем типичные ситуации, в которых используется интегрирование по частям.
1) Под знаком интеграла стоит 
, 
, 
, умноженные на многочлен.
2) Интеграл вида 
, 
, 
.
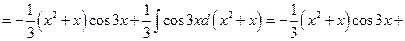
3) Интеграл вида 
, 
.
Обозначим F (x) произвольную первообразную функции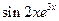 
, получим
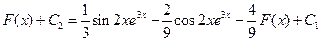
Выразим
.
Интегрирование рациональных функций
Рациональной функцией, или рациональной дробью, называется выражение вида 
, где 
и 
− многочлены степени n и m соответственно. Если n 
m, дробь называется неправильной, а если n 
m, то правильной. Неправильную рациональную дробь можно записать в виде суммы многочлена и правильной дроби. Для этого используется следующая процедура деления с остатком многочлена на многочлен (алгоритм Евклида).
Пусть 
, 
при этом 
, n m. Умножим на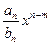 
и вычтем получившееся выражение из 
. В результате получим некоторый многочлен 
, степень которого строго меньше 
, и при этом 
. Если степень 
все еще больше 
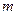, применим описанный прием уже к многочлену , и так до тех пор, пока не получим «в остатке» многочлен степени строго меньше 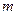. Эта процедура деления разобрана далее на нескольких примерах (деление «уголком»).
Правильная рациональная дробь называется простой, если она принадлежит к одному из нижеперечисленных типов
Примеры простых дробей:
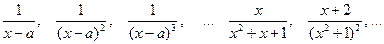
Любая правильная рациональная дробь может быть представлена как сумма простых дробей с подходящими коэффициентами. Такое разложение находят методом неопределенных коэффициентов, который мы проиллюстрируем на одном конкретном примере. Рассмотрим функцию:
. (1)
Составим комбинацию простых дробей, в знаменателях которых присутствуют все возможные делители знаменателя исходной функции:
После приведения этих пяти дробей к общему знаменателю получим:
(2)
Приравняв числители (1) и (2), получим уравнение
(3)
Соотношение (3) должно быть выполнено при всех значениях х. Подставим в (3) пять (по числу неизвестных коэффициентов A, B, C, D, E) различных значений х и получим систему уравнений на A, B, C, D, E:
Можно показать, что у такой системы всегда существует единственное решение. Решив эту систему (например, методом Гаусса), получим требуемое представление 
Интегрирование любой простой дроби всегда сводится к интегрированию табличных функций. Приведем несколько наиболее типичных примеров:
1) 
2) 
3) 
.
Кратный неразложимый квадратный многочлен в знаменателе дроби.
1 способ. Интегрирование по частям.
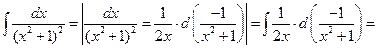
2 способ. Замена переменной. 
= 