Если функция f (x, y) определена в некоторой области D, то ее частные производные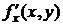 
и 
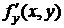тоже будут определены в той же области или ее части. Будем называть эти производные частными производными первого порядка.
Производные этих функций будут частными производными второгопорядка: 
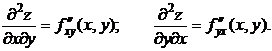
Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков. Частные производные вида 
и т.д. называются смешанными производными.
Теорема (Шварц). Двесмешанные частные производные одного порядка одной и той же функции, отличающиеся лишь порядком дифференцирования, в случае, когда они являются непрерывными функциями, равны между собой (например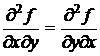 
).
Т.е. частные производные высших порядков не зависят от порядка дифференцирования.
Пример 14. Найти все частные производные второго порядка функции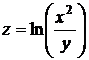 
.
Решение. Используя свойства логарифмов преобразуем выражение 
. Найдем частные производные первого порядка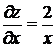 
и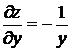 
. Найдем частные производные второго порядка 
, 
, 
, 
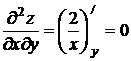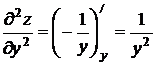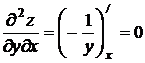.[10]
Дифференциалы высших порядков
Аналогично определяются дифференциалы высших порядков.
…………………
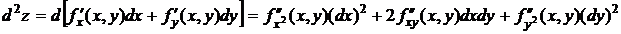
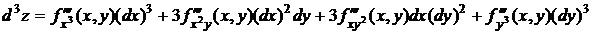
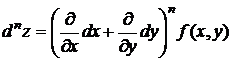
Здесь n – символическая степень производной, на которую заменяется реальная степень после возведения в нее стоящего в скобках выражения.
Пример 15. Для функци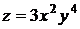и 
найти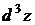 
.
Решение. Найдем все частные производные третьего порядка. 
, 
, 
, 
; 
, 
, 
, 
, 
.
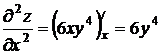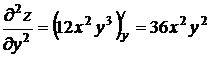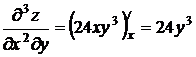Подставим полученные производные в формулу =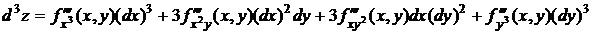
= 
+ 
+ 
+ 
.
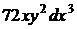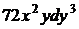Приложения дифференцирования функции
Нескольких переменных
Касательная плоскость и нормаль к поверхности
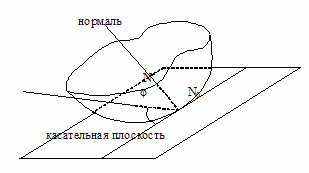Пусть N и N 0 – точки данной поверхности. Проведем прямую NN 0. Плоскость, которая проходит через точку N 0, называется касательной плоскостью к поверхности, если угол между секущей NN 0 и этой плоскостью стремится к нулю, когда стремится к нулю расстояние NN0.
Нормалью к поверхности в точке N0 называется прямая, проходящая через точку N0 перпендикулярно касательной плоскости к этой поверхности.
Рис.21
Замечание. В какой – либо точке поверхность имеет, либо только одну касательную плоскость, либо не имеет ее вовсе.
Пусть поверхность задана уравнением z = f (x, y), запишем её в неявном виде 
, где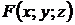 
– функция, дифференцируемая в точке 
. Тогда касательная плоскость существует и имеет уравнение
.
Уравнение нормали к поверхности в этой точке: 
Пример 17. Найти уравнения касательной плоскости и нормали к поверхности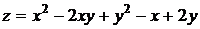 
в точке М (1, 1, 1).
Решение. Запишем данную функцию в неявном виде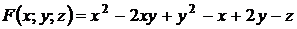 
. Найдём 
,
, 
.
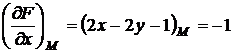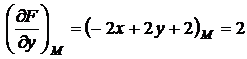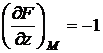Уравнение касательной плоскости: 
.
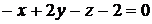Уравнение нормали: 
Приближенные вычисления с помощью полного дифференциала
Пусть функция f (x, y) дифференцируема в точке (х, у). Найдем полное приращение этой функции: 
,
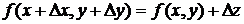
Если подставить в эту формулу выражение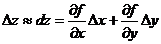 
, то получим приближенную формулу: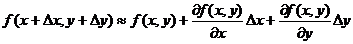 
Пример 18. Вычислить приближенно значение 
, исходя из значения функции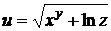 
при x = 1, y = 2, z = 1.
Решение. Из заданного выражения определим Dx = 1,04 – 1 = 0,04, Dy = 1,99 – 2 = -0,01, Dz = 1,02 – 1 = 0,02.
Найдем значение функции u (x, y, z) =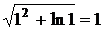 
.
Находим частные производные: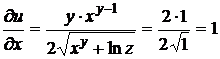 
;
; 
.
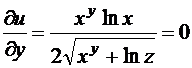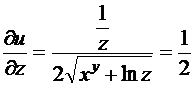Полный дифференциал функции u равен:
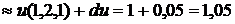
Точное значение этого выражения: 1,049275225687319176.