Вопрос 6. Линейное ДУ первого порядка. Уравнение Бернулли

Df. Уравнение вида y' + Р(х)у = q(x), (1)

где р(х) и q(x) определены на интервале (а,b), называется линейным дифференциальным уравнением первого порядка. Если q(x)=0, то уравнение (1) принимает вид у' + р(х)у = 0 и называется линейным однородным, в противном случае его называют линейным неоднородным.

Примечание. Линейное однородное дифференциальное уравнение является частным случаем уравнения с разделяющимися переменными у' = g(x)h(y), в ко- ором принимаем g(x) = , = у. Отметим также, что функция у(х)=0 является одним из решений такого уравнения. Решение подобного типа называют тривиальным.

Метод интегрирующего множителя

Если функция является решением уравнения (1), то выполняется равенство

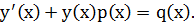Умножим обе части последнего равенства на функцию 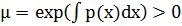, называемую интегрирующим множите­лем. Получим

у’(х)ехр(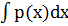) + р(х)у(х)ехр(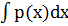) = q(х)ехр().

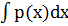Выражение в левой части полученного равенства можно записать в виде

(y(x)ехр(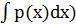 '. Откуда (у(х)ехр 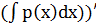= ехр(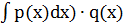

Интегрируя обе части полученного равенства, имеем

у(x)ехр 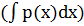= 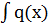exp 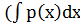))dx + С, где С — произвольная постоянная. Получим у(х) = ехр(- )( exp 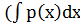))dx + С).

Теорема (существование и единственность решения задачи Коши)

Если функции р(х) и q(x) непрерывны в интервале (а, b) и 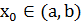, то задача Коши

у' + р(х)у = q(x), у(х₀) = у₀, имеет единственное решение, которое определено на интервале (а, b).

Примечание. Иными словами, через каждую точку (x₀, у₀) бесконечной по­лосы (а,b) проходит только одна интегральная кривая линейного неоднород­ного дифференциального уравнения первого порядка.

Df. Уравнение Бернулли имеет вид у' + р(х)у = q(x)yⁿ,(2)

где р(х) и q(х) — определенные и непрерывные на интервале (а, b), функ­ции; n 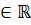\{0; 1}.

Примечание. Если положить n = 0, то получим линейное неоднородное урав­нение вида у' + р(х)у = q(x), а если п = 1, то получим линейное однородное урав­нение вида у' + (х)у = 0, где (х) = р(х) - q(x).

Для каждого п > 0 функция у(х) = 0 является одним из решений уравнения Бернулли.

Утверждение (приведение уравнения Бернулли к линейному) Дифференциальное уравнение Бернулли (2) с помощью замены перемен­ных z = у^1-n приводится к линейному неоднородному дифференциальному уравнению вида z' + (1 - п)р(х)z = (1 - n)q(x).

 

Вопрос 7. Уравнение Риккати. Уравнение Абеля. ДУ, приводящие к этим уравнениям

Df. Ур-ние вида называется Общим уравнением Риккати.

– специальное уравнение Риккати, где

Если A(x)=0, то (1)Линейное Общее Дифференциальное Уравнение 1-го порядка.

Если С(x)=0, то (1) ДУ Бернулли, n=2

Если A(x)=C(x)=0, то (1) Линейное Однородное ДУ

Если A=В=0, то (1) неполное ДУ с разделяющимися переменными

Если В=С=0, то уравнение с разделяющими переменными.

Теорема: Если - частное решение ДУ(1), то это уравнение интегрируется в квадратурах.

Cв-ва ур-ния Риккати:

1. 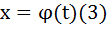, где 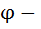непрерывная дифференцируемая функция, x – старая, t – новая.

– инвариантно

2. Преобразование искомой функции: 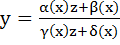(11)

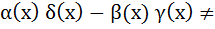0

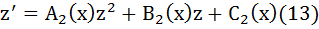
3. Коэффициент при квадрате искомой функции всегда можно сделать

Теорема: Если известны два частных решения уравнения Риккати, то его общее решение находится с помощью не более чем одной квадратуры.

Док-во: Пусть частные решения уравнения (1). Тогда для решения уравнения известно одно частное решение

. Следовательно (24) решение (*).

Уравнение(*) с учетом замены (24) интегрируемо в квадратурах, причем число квадратур не более одной.

Теорема: Если известно 3 частных решения, то его общее решение находится без квадратуры.

Теорема: Сложное отношение 4-х частных решений уравнений Риккати есть постоянное

Уравнение Абеля.

– уравнение Абеля 1-го рода

– уравнение Абеля 2-го рода

Теорема: Пусть известно, что 4-ре функции являются частными решениями уравнения Абеля. Тогда мы можем установить вид этого уравнения, но не сможем его проинтегрировать.

Вопрос 8. Уравнения в полных дифференциалах. Интегрирующий множитель

Df. Дифференциальное уравнение вида М(х, y)dx + N(x, y)dy = О(1), где функции М(х, у) и N(x,у) определены в некоторой области D, на­зывается уравнением в полных дифференциалах, если: 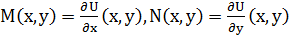для некоторой функции U(x,у).

Замечание: Выражение называется полным дифференциалом функции U(x,y) и обозначается символом dU(x,у). Иначе говоря, дифференциальное уравнение (1) является уравнением в полных дифференциалах, если его левая часть есть полный дифференциал некоторой функции. Такое урав­нение можно записать в виде dU(x, у) = 0.

Утверждение: ( необх и достаточное условие уравнения в полных дифференциалах)

Пусть функции М(х,у), N(x, у) и частные производные ,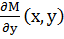

непрерывны в связной области . Уравнение (1) является

дифференциальным уравнением в полных дифференциалах тогда и только тогда, когда для каждой пары (х, у) 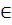D выполняется условие: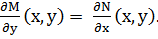

Утверждение (уравнение для определения интегрирующего множителя)

Если функция 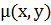является интегрирующим множителем уравнения (1), то она удовлетворяет дифференциальному уравнению в частных производных:

 

Вопрос 9. Теорема существования и единственности. Доказательство теоремы существования и единственности для одного уравнения. Теорема Коши для комплексной плоскости.

(1); и

-задача Коши для 1ого векторного уравнения//если начальные уравнения, то задача Коши для системы n скалярных уравнений.

Введем вектор:

Решением системы наз. Вектор-функция , которая определена и непрерывно дифференцируема на некотором интервале Р=()(можно на отрезке и полуинтервале) и удовлетворяет системе (1).

Пусть решение системы (1) определённое на интервале Р. Интегральной кривой системы (1) наз. кривая () в (n+1)-мерном пространстве (количество уравнений + количество переменных из (1)) с координатами .

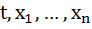{Геометрическая интерпретация задачи Коши}:

Требуется найти интегральную кривую системы , проходящую через точку . Вектор 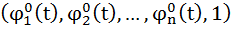касается интегральной кривой 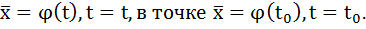В силу системы получим в рассмотренной области поле. Интегральные кривые системы принадлежат этому векторному полю, то есть касаются векторов этого поля, в каждой точке которого, верно и обратное, а именно: любая непрерывно – дифференцируемая прямая 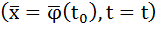принадлежащая данному векторному полю является интегральной кривой системы

Теорема решения задачи Коши: Пусть имеется задача Коши , если и 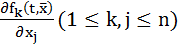определены и непрерывно дифференцируемы в некоторой области G и т. С координатами (, тогда:

1) Решение задачи Коши 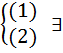на некотором интервале Р=(;

2) Решение задачи Коши ! на Р, т.е. если мы имеем 2 решения , то на Р эти решения .

Рассм. Задачу Коши для 1ого уравнения:

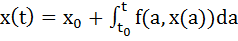
Применим метод последовательных приближений:

{ Геометрическая интерпретация основной теоремы }:

В условии теоремы через каждую точку области G проходит интегральная кривая и при этом только одна.

Лемма: Задача Коши 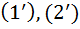эквивалентна системе интегральных уравнений: , т.е. 1. любое решение удовлетворяет условию (3)

2. любая непрерывная на некотором интервале 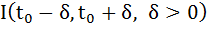решение уравнения (3) является решением задачи Коши .

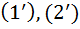Df. Пусть для любой функции x(t) M поставлена в соответствии функция , тогда мы говорим, что задан оператор А, переводящий функцию x(t) в функцию g(t),

 

3. компл плоскость

Df. Функция называется аналитической в точке , если она разлагается в степенной ряд сходится в нем в окрестности точки .

Df. Функция f(z,w) называется аналитической в точке , если она разлагается в данный степенной ряд: сходится в окрестности точки .

Теорема Коши: Пусть функция f(z,w) аналтична в т , тогда решение задачи Коши аналитично в точке и единственно в этой точке.