Общее уравнение плоскости

Формулы вычисления смешанного произведения векторов

Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов.

Смешанное произведение векторов a = {a_x; a_y; a_z}, b = {b_x; b_y; b_z} и c = {c_x; c_y; c_z} в декартовой системе координат можно вычислить, используя следующую формулу:

a · [b × c] =	ax	ay	az
bx	by	bz
cx	cy	cz

 

• Геометрический смысл смешанного произведения.

Модуль смешанного произведения трех векторов a, b и сравен объёму параллелепипеда, образованного этими векторами:

V_парал = |a · [b × c]|

• Геометрический смысл смешанного произведения.

Объем пирамиды образованной тремя векторами a, b и сравен одной шестой части от модуля смешанного произведения этих векторов:

Vпир =		|a · [b × c]|

Условия компланарности векторов

• Для 3-х векторов. Три вектора компланарны если их смешанное произведение равно нулю.
• Для 3-х векторов. Три вектора компланарны если они линейно зависимы.
• Для n векторов. Вектора компланарны если среди них не более двух линейно независимых векторов.

10) Определение. Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними.

Скалярное произведение в координатах равно сумме произведений соответствующих координат, поэтому,

Определение. Векторным произведением вектора на вектор называется третий вектор , который удовлетворяет следующим трем условиям:

1) и ;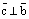

2) тройка векторов является правоориентированной;

3) .

Векторное произведение в координатах имеет вид

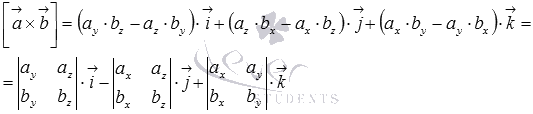
смешанное произведение векторов равно определителю матрицы третьего порядка, строками которой являются координаты умножаемых векторов, то есть,
.

 

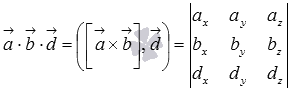Общее уравнение плоскости

Любую плоскость можно задать уравнением плоскости первой степени вида

A x + B y + C z + D = 0

где A, B и C не могут быть одновременно равны нулю.

 

Уравнение плоскости, проходящие через 3 заданные точки

 

12) нормальное уравнение плоскости или уравнение плоскости в нормальном виде. Нормальное уравнение плоскости иногда называют нормированным уравнением плоскости.

Расстояние от точки до плоскости – это длина перпендикуляра, опущенного из заданной точки к заданной плоскости.

Итак, алгоритм для нахождения расстояния от точки до плоскости следующий:

· составляем уравнение прямой a, которая проходит через точку М₁ и перпендикулярна к плоскости ;

· находим координаты 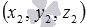точки H₁ - точки пересечения прямой a и плоскости ;

· вычисляем расстояние от точки М₁ до плоскости по формуле .

Второй способ, подходящий для нахождения расстояния от точки до плоскости .

Так как в прямоугольной системе координат Oxyz нам задана плоскость , то мы можем получить нормальное уравнение плоскости в виде . Тогда расстояние от точки до плоскости вычисляется по формуле .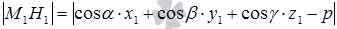

13) Если все числа А, В, С и D отличны от нуля, то общее уравнение плоскости 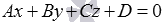называется полным. В противном случае, общее уравнение плоскости называется неполным.

14) прямая в пространстве в прямоугольной системе координат Oxyz может быть задана системой из уравнений двух пересекающихся плоскостей .

Параметрические уравнения прямой в пространстве имеют вид 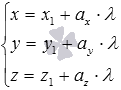, где x₁, y₁ и z₁ – координаты некоторой точки прямой, a_x, a_y и a_z (a_x, a_y и a_z одновременно не равны нулю) - соответствующие координаты направляющего вектора прямой, а - некоторый параметр, который может принимать любые действительные значения.

Разрешив каждое из параметрических уравнений прямой вида 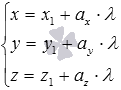относительно параметра , легко перейти к каноническим уравнениям прямой в пространстве вида .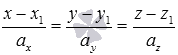

Канонические уравнения прямой в пространстве определяют прямую, проходящую через точку , а направляющим вектором прямой является вектор .

15)

Начнем с приведения общего уравнения прямой к каноническому уравнению прямой вида .

Если , то переносим слагаемое в правую часть равенства с противоположным знаком . В левой части равенства выносим А за скобки . Полученное равенство можно записать как пропорцию вида .

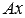Если , то оставляем в левой части общего уравнения прямой только слагаемое , а остальные переносим в правую часть с противоположным знаком: 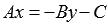. Теперь выносим в правой части равенства –B за скобки и записываем полученное равенство в виде пропорции .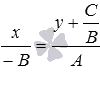

 

16) Существует три варианта взаимного расположения прямой и плоскости:

1) прямая пересекает плоскость в некоторой точке ;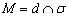

2) прямая параллельна плоскости: ;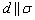

3) прямая лежит в плоскости: .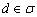

Прямая пересекает плоскость тогда и только тогда, когда её направляющий вектор не ортогонален вектору нормали плоскости.

Из утверждения следует, что скалярное произведение вектора нормали и направляющего вектора будет отлично от нуля: .

В координатах условие запишется следующим образом:

Если же данные векторы ортогональны, то есть если их скалярное произведение равно нулю: , то прямая либо параллельна плоскости, либо лежит в ней:

Разграничим данные случаи.

Если прямая параллельна плоскости, то точка (а, значит, и ЛЮБАЯ точка данной прямой) не удовлетворяет уравнению плоскости: .

Таким образом, условие параллельности прямой и плоскости записывается следующей системой:

Если прямая лежит в плоскости, то точка (а, значит, и ЛЮБАЯ точка данной прямой) удовлетворяет уравнению плоскости: .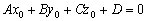

Аналитические условия данного случая запишутся похожей системой:

17) Общим уравнением второго порядка называется уравнение вида:

Ax²+2Bxy+Cy²+2Dx+2Ey+F=0

где коэффициенты A,B,C одновременно не равны нулю.
Линии, определяемые такими уравнениями, называются кривыми второго порядка.

Окружностью называется фигура, состоящая из всех точек плоскости, находящихся от данной точки на данном расстоянии.

"Уникальные" свойства окружности

1.Два угла с вершинами на окружности, опирающиеся на одну и ту же дугу, равны.

2.Касательные к окружности, проведенные из одной точки, равны.

3.Из всех замкнутых кривых данной длины окружность ограничивает область максимальной площади.

4.Из всех замкнутых кривых, для которых длины всех хорд не превосходят заданной величины, окружность ограничивает область максимальной площади.

5.Любые две дуги окружности равной длины можно совместить.

Это свойство называется самоконгруэнтностью. На плоскости им, кроме окружности, обладает только прямая. Если кривая может не лежать в плоскости, оно задает также винтовую линию.

Однако замкнутых самоконгруэнтных кривых, отличных от окружности, не существует. Благодаря этому свойству меч, имеющий форму дуги окружности, можно вставлять и вынимать из ножен той же формы.

6.При любом расположении двух равных окружностей на плоскости они имеют не больше двух общих точек.

7.Любая прямая, проходящая через центр окружности, является ее осью симметрии.

Эллипс - замкнутая кривая линия, полученная сечением конуса или цилиндра плоскостью.

Рассмотрим свойства эллипса.

Свойство 10.1.

Эллипс пересекает каждую из осей координат в двух точках.

Сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равная удвоенной большей полуоси.

Эллипс имеет две взаимно перпендикулярные оси симметрии.

Эллипс имеет центр симметрии.

Эллипс может быть получен сжатием окружности.

 

18) В новой системе координат, которую называют также канонической, уравнение гиперболы имеет вид

Это уравнение называется каноническим уравнением гиперболы.

Отметим следующие свойства гиперболы.

Свойство 10.6.

Гипербола не имеет общих точек с осью Oy, а ось Ox пересекает в двух точках A (a; 0) и B (– a; 0), которые называются вершинами гиперболы.

Гипербола имеет две взаимно перпендикулярные оси симметрии.

Гипербола пересекается с прямой y = kx при в двух точках. Если 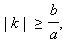то общих точек у прямой и гиперболы нет.

Свойства параболы

Парабола имеет ось симметрии.

Парабола расположена в полуплоскости x ≥ 0.

 

19)

Общее уравнение поверхности второго порядка
Ax2+By2+Cz2+2Fyz+2Gzx+2Hxy+2Px+2Qy+2Rz+D=0,
где x, y, z − координаты точек поверхности, A, B, C, … − действительные числа.

Сфе́ра (др.-греч. σφαῖρα — мяч, шар^[1]) — это геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки (центра сферы).

Эллипсо́ид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей.

В математике гиперболоид — это вид поверхностивторого порядка в трёхмерном пространстве, задаваемый в декартовых координатах уравнением

{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1} (однополостный гиперболоид),

где a и b — действительные полуоси, а c — мнимая полуось;

или

{\displaystyle -{x^{2} \over a^{2}}-{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1} (двуполостный гиперболоид),

где a и b — мнимые полуоси, а c — действительная полуось.

Параболо́ид ― тип поверхности второго порядка в трёхмерном евклидовом пространстве. Параболоид может быть охарактеризован как незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка.

Канонические уравнения параболоида в декартовых координатах:

{\displaystyle z=tx^{2}+uy^{2}},

где {\displaystyle t} и {\displaystyle u} — действительные числа не равные нулю одновременно. При этом

· если {\displaystyle t} и {\displaystyle u} одного знака, то параболоид называется эллиптическим, частный случай эллиптического параболоида {\displaystyle t=u,} в этом случае поверхность принято называть параболоидом вращения;

· если {\displaystyle t} и {\displaystyle u} разного знака, то параболоид называется гиперболическим;

· если один из коэффициентов равен нулю, то параболоид называется параболическим цилиндром.

· Цилиндрической поверхностью называется поверхность, которая в некоторой декартовой системе координат определяется уравнением, в котором не фигурирует одна из переменных:

F (x, y) = 0, F (x, z) = 0 или F (y, z) = 0.