ВЫСШАЯ МАТЕМАТИКА
Методические указания и контрольная работа №2
Для студентов Гродненского филиала кафедры
«Информационные системы и технологии»
МИДО БНТУ
специальность
«Экономика и управление на предприятии»
Номер варианта задания совпадает с последней цифрой номера зачётной книжки студента (цифра 0 соответствует 10-му варианту)
Решение типового варианта.
Задача 1. Найти предел последовательности
а)  б)
б)  в)
в)  г)
г) 
д)  е)
е)  ж)
ж) 
Решение.
а) Числитель и знаменатель дроби являются бесконечно большими последовательностями, т.е. имеет место неопределённость вида  . Разделим числитель и знаменатель на старшую степень дроби, т.е. на
. Разделим числитель и знаменатель на старшую степень дроби, т.е. на  и используя теоремы об операциях над пределами, получим
и используя теоремы об операциях над пределами, получим  б) В знаменателе имеется неопределённость вида
б) В знаменателе имеется неопределённость вида  . Умножив числитель и знаменатель дроби на выражение
. Умножив числитель и знаменатель дроби на выражение  и, после выполнения тождественных преобразований, разделив числитель и знаменатель на
и, после выполнения тождественных преобразований, разделив числитель и знаменатель на  , получим
, получим


в) Здесь имеет место неопределённость вида  . Разделим числитель и знаменатель дроби на
. Разделим числитель и знаменатель дроби на  :
:

г) В данном примере имеется неопределённость вида  . Преобразуем общий член последовательности:
. Преобразуем общий член последовательности: 

д) Числовая последовательность  представляет собой сумму членов двух геометрических прогрессий. Применяя формулу суммы первых
представляет собой сумму членов двух геометрических прогрессий. Применяя формулу суммы первых  членов геометрической прогрессии, получим:
членов геометрической прогрессии, получим:

Тогда 

е) Поскольку  , а
, а  , то
, то

ж) Учитывая, что  , имеем:
, имеем: 

Задача 2. Найти предел функции не пользуясь правилом Лопиталя
а)  б)
б)  в)
в)  г)
г) 
д)  е)
е)  ж)
ж)  з)
з) 
Решение.
а) Поскольку пределы числителя и знаменателя равны нулю, мы имеем дело с неопределённостью вида  . Чтобы избавиться от неё, разложим числитель и знаменатель на множители и сократим дробь на
. Чтобы избавиться от неё, разложим числитель и знаменатель на множители и сократим дробь на  :
: 
б) Для раскрытия неопределённости вида  сделаем следующие преобразования:
сделаем следующие преобразования: 
в) Сделаем замену  , тогда
, тогда  и
и  при
при  . Отсюда
. Отсюда 
г) Положим  , отсюда получаем, что
, отсюда получаем, что  и
и  при
при  . Таким образом
. Таким образом

д) Имеем  .
.
Сделаем замену  , отсюда
, отсюда  и
и  при
при  . Тогда, учитывая, что
. Тогда, учитывая, что  , находим
, находим 
е) В данном примере предел основания степени равен 1, а показатель стремится к бесконечности, значит имеет место неопределённость вида  . Используя второй замечательный предел, получаем:
. Используя второй замечательный предел, получаем:

ж) Положим  , тогда
, тогда  и
и  при
при  . Следовательно
. Следовательно

з) Здесь имеется неопределённость вида  . Для её раскрытия приведём дроби к общему знаменателю:
. Для её раскрытия приведём дроби к общему знаменателю:

Задача 3. Найти производную заданной функции
а) 
б) 
в) 
г) 
Решение.
Применяя правила дифференцирования и используя таблицу производных, находим:
а) 




б)



в) 
Прологарифмируем обе части:


Продифференцируем обе части



г) Дифференцируя обе части равенства, имеем

Т.к. по условию  , то получаем
, то получаем

Задача 4. Дана функция  в точке
в точке  и
и 
а) Установить является ли функция непрерывной в этих точках
б) Найти пределы слева и справа
в) Сделать схематический чертеж
Решение:
В точке x = 0 функция непрерывна, т.е.

В точке x = 2
предел слева

предел справа

Схематичный чертеж на рис 1
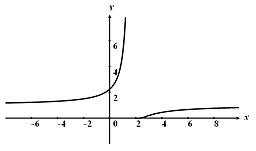
Рисунок 1
Задача 5.
 x + 1, если x ≤ 0
x + 1, если x ≤ 0
Дана функция y = x2, если 0 > x ≤ 2
½ x + 3, если x ≥ 2
Найти точки разрыва, если они существуют сделать чертеж.
Решение:
График функции изображен на рисунке

В точке x = 0 разрыв первого рода т.к. 

В точке x = 2 разрыва нет. 
В остальных точках функция непрерывна.
Задача 6. Используя правило Лопиталя вычислить пределы:
а) 




б) 
в) 


г) 

Имеем неопределённость вида  . Положим
. Положим  и прологарифмируем обе части равенства
и прологарифмируем обе части равенства 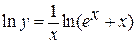
Найдём

Поскольку 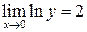 , то
, то 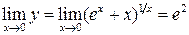
Задача 7. Исследовать функцию и построить её график: 
Решение: Приведём схему полного исследования функции
1. Область определения функции
2. Чётность, нечётность, переодичность
3. Точки разрыва функции; приделы при  концам промежутков области определения; асимптоты
концам промежутков области определения; асимптоты
4. Интервалы возрастания и убывания функции, точки экстремума; вычислить значения экстремумов
5. Интервалы выпуклости и точки перегиба
6. Точки пересечения графика с осями координат
7. График
1. Функция  определена, если
определена, если  , значит
, значит 
2. Т.к. область определения функции  не является симметричным множеством относительно начала координат, то функция
не является симметричным множеством относительно начала координат, то функция  не может быть чётной, нечётной и периодической.
не может быть чётной, нечётной и периодической.
3. Найдём пределы функций при  концам промежутков области определения
концам промежутков области определения

Аналогично, получаем что 
Поскольку
 , то точка
, то точка  - точка разрыва второго рода, а
- точка разрыва второго рода, а  - вертикальная асимптота.
- вертикальная асимптота.
Найдём наклонные асимптоты  , где
, где


Следовательно,  - уравнение наклонной асимптоты
- уравнение наклонной асимптоты
4. Производная
 определена на
определена на 
Поскольку  при
при  ,
,  , то это критические точки функции. Так как
, то это критические точки функции. Так как
 при
при 

 при
при 

 |
то на интервалах  ,
, 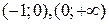 функция возрастает, а на интервале
функция возрастает, а на интервале
 - убывает.
- убывает.
При  функция имеет максимум, т.к. переходе через эту точку
функция имеет максимум, т.к. переходе через эту точку  меняет знак с «+» на «
меняет знак с «+» на « ».
».
 , значит точка
, значит точка 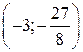 - точка максимума.
- точка максимума.
5. Находим вторую производную
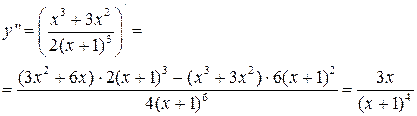
Она определена для  . Поскольку
. Поскольку  при
при  , то определив знак
, то определив знак  на каждом из интервалов
на каждом из интервалов 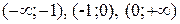 , получим, что для
, получим, что для 
 , график выпуклый; для
, график выпуклый; для  график вогнутый.
график вогнутый.
При переходе через точку  производная
производная  меняет знак, поэтому
меняет знак, поэтому  - точка перегиба, причём
- точка перегиба, причём  .
.
6. График функции пересекает координатные оси в т.  .
.

Задача 8. Разложить число 100 на два слагаемых так, чтобы их произведение было наибольшим.
Решение. Пусть  - первое слагаемое,
- первое слагаемое,  будет второе слагаемое.
будет второе слагаемое.
Произведение этих слагаемых даёт функцию  .
.
По условию задачи  . Найдём экстремумы этой функции
. Найдём экстремумы этой функции  ,
,  ,
,
то при  функция достигает максимума.
функция достигает максимума.

 следовательно функция принимает наибольшее значение в критической точке
следовательно функция принимает наибольшее значение в критической точке  .
.
Ответ: Произведение двух слагаемых будет наибольшее, если они равны 50. 
Задача 9. Найти неопределённые интегралы. В пунктах a) и b) проверить результаты дифференцированием.
a. 
Преобразуем подынтегральную функцию таким образом, чтобы в числителе получилась производная знаменателя:

Проверим полученный результат:

b. 
Воспользуемся методом интегрирования по частям, основанном на следующей формуле:


Выполним проверку результата:

c. 
Подынтегральная функция представляет собой рациональную дробь. Разложим её знаменатель на множители:  тогда:
тогда:

Приведя правую часть последнего равенства к общему знаменателю, и приравняв числители дробей, получим тождество:

Найдём искомые коэффициенты:
а) полагая  , получаем
, получаем  , откуда
, откуда  ;
;
б) полагая  , получаем
, получаем  , откуда
, откуда  ;
;
в) полагая  , получаем
, получаем  , откуда
, откуда  ;
;
Подставив найденные коэффициенты в разложение подынтегральной функции на простейшие дроби, получим:

d. 
Подынтегральная функция представляет собой интеграл вида:

Где  - рациональная функция;
- рациональная функция;  - целые положительные числа. С помощью подстановки
- целые положительные числа. С помощью подстановки  (здесь
(здесь  - наименьшее общее кратное (НОК) знаменателей
- наименьшее общее кратное (НОК) знаменателей  ) данный интеграл приводится к интегралу от рациональной функции.
) данный интеграл приводится к интегралу от рациональной функции.

Задача 10. Вычислить несобственные интегралы или доказать их расходимость:
a) 
b) 
Задача 11. a) Вычислить площадь фигуры, ограниченной линиями
 и
и 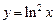 .
.
Построим графики данных кривых:

Найдём точки пересечения данных кривых:

 Тогда по формуле
Тогда по формуле
 имеем:
имеем:



Окончательно имеем:
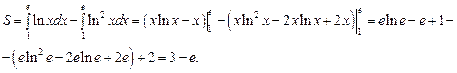
Задачи для контрольной работы №2.
Задача 1. Найти предел последовательности
1. а)  б)
б)  в)
в) 
г)  д)
д)  е)
е)  ж)
ж) 
2. а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е)  ж)
ж) 
3. а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е)  ж)
ж) 
4. а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е)  ж)
ж) 
5. а)  б)
б)  в)
в)  г)
г) 
д)  е)
е)  ж)
ж) 
6. а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е)  ж)
ж) 
7 а)  б)
б)  в)
в)  г)
г) 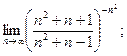
д)  е)
е)  ж)
ж) 
8. а)  б)
б)  в)
в) 
г)  д)
д)  е)
е)  ж)
ж) 
9. а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е)  ж)
ж) 
10. а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е)  ж)
ж) 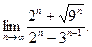
Задача 2. Найти предел функции не пользуясь правилом Лопиталя;
1. а)  б)
б)  в)
в)  г)
г) 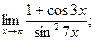
д)  е)
е)  ж)
ж) 
2. а)  б)
б)  в) г)
в) г) 

д)  е)
е)  ж)
ж) 
3. а)  б)
б)  в)
в)  г)
г) 
д)  е)
е)  ж)
ж) 
4. а)  б)
б) 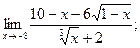 в)
в)  г)
г) 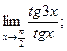
д)  е)
е) 

5. а)  б)
б)  в)
в)  г)
г) 
д)  е)
е)  ж)
ж) 
6. а)  б)
б)  в)
в)  г)
г) 
д)  е)
е)  ж)
ж) 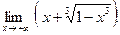
7. а)  б)
б)  в)
в)  г)
г) 
д)  е)
е)  ж)
ж) 
8. а)  б)
б)  в)
в)  г)
г) 
д)  е)
е)  ж)
ж) 
9. а)  б)
б)  в)
в)  г)
г) 
д)  е)
е)  ж)
ж) 
10. а)  б)
б)  в)
в) 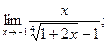 г)
г) 
д)  е)
е)  ж)
ж) 
Задача 3. Найти производные данных функций
1.
а)  б)
б) 
в)  г)
г) 
2.
а)  б)
б) 
в)  г)
г) 
3.
а)  б)
б) 
в)  г)
г) 
4.
а)  б)
б) 
в)  г)
г) 
5.
а)  б)
б) 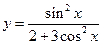
в)  г)
г) 
6.
а)  б)
б) 
в) 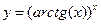 г)
г) 
7.
а)  б)
б) 
в)  г)
г) 
8.
а)  б)
б) 
в)  г)
г) 
9.
а)  б)
б) 
в)  г)
г) 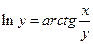
10.
а)  б)
б) 
в)  г)
г) 
Задача 4. Заданы функции  и два значения аргумента
и два значения аргумента  и
и  .
.
Требуется
а) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента;
б) в случае разрыва функции найти ее пределы слева и справа;
в) сделать схематический чертеж
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
Задача 5. Задана функция  . Найти точки разрыва функции, если они существуют. Сделать чертеж.
. Найти точки разрыва функции, если они существуют. Сделать чертеж.
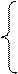
 , если
, если 
1. 
 , если
, если 
 , если
, если 

 , если
, если 
2. 
 , если
, если 
 , если
, если 

 , если
, если 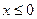
3. 
 , если
, если 
 , если
, если 

 , если
, если 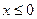
4. 
 , если
, если 
 , если
, если 

 , если
, если 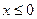
5. 
 , если
, если 
 , если
, если 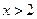

 , если
, если 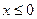
6. 
 , если
, если 
 , если
, если 

 , если
, если 
7. 
 , если
, если 
 , если
, если 

 , если
, если 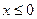
8. 
 , если
, если 
 2, если
2, если 
 , если
, если 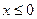
9. 
 , если
, если 
2, если 

 , если
, если 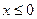
10. 
 , если
, если 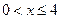
1, если 
Задача 6. Используя правило Лопиталя вычислить пределы:
1. а)  б)
б) 
2. а)  б)
б) 
3. а)  б)
б) 
4. а)  б)
б) 
5. а)  б)
б) 
6. а)  б)
б) 
7. а)  б)
б) 
8. а)  б)
б) 
9. а)  б)
б) 
10. а)  б)
б) 
Задача 7. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить её график.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
Задача 8.
1. Требуется изготовить из жести ведро без крышки данного объема V цилиндрической формы. Каковы должны быть высота цилиндра и радиус основания, чтобы на изготовление ведра ушло наименьшее количество материала?
2. Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиуса  ?
?
3. При каких линейных размерах закрытая цилиндрическая банка данной вместимости V будет иметь наименьшую полную поверхность?
4. Требуется изготовить открытый цилиндрический