Содержание
численное интегрирование формула программирование
Введение
Методы численного интегрирования
2. Квадратурные формулы
3. Автоматический выбор шага интегрирования
Заключение
Библиографический список
Введение
Цель реферата состоит в изучение и сравнительный анализ методов численного интегрирования функций; реализация этих методов в виде машинных программ на языке высокого уровня и практическое решение задач численного интегрирования на ЭВМ.
При решении инженерных задач часто возникает необходимость в вычислениях значений определенного интеграла вида
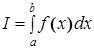. (1)
Если функция непрерывна на отрезке [ a, b ] и ее первообразная может быть определена через известную функцию, то вычисление такого интеграла производится по формуле Ньютона – Лейбница:
.
В инженерных задачах получить значение интеграла в аналитическом виде удается редко. Кроме того, функция f (x) может быть задана, например, таблицей экспериментальных данных. Поэтому на практике для вычисления определенного интеграла используют специальные методы, в основе которых лежит аппарат интерполирования.
Идея таких методов заключается в следующем. Вместо того, чтобы вычислять интеграл по формуле (1), сначала вычисляют значения функции f (xi) = yi в некоторых узлах xi Î[ a, b ]. Затем выбирается интерполяционный многочлен P (x), проходящий через полученные точки (xi, yi), который используется при вычислении приближенного значения интеграла (1):
.
При реализации такого подхода формулы численного интегрирования принимают следующий общий вид:
, (2)
где 
- узлы интерполирования, Ai – некоторые коэффициенты, R – остаточный член, характеризующий погрешность формулы. Заметим, что формулы вида (2) называют квадратурными формулами.
|
|
Геометрический смысл численного интегрирования состоит в вычислении площади криволинейной трапеции, ограниченной графиком функции f (х),осью абсцисс и двумя прямыми х = а и х = b. Приближенное вычисление площади приводит к отбрасыванию в квадратурных формулах остаточного члена R, характеризующего погрешность метода, на которую дополнительно накладывается вычислительная погрешность.
Методы численного интегрирования
В прикладных исследованиях часто возникает необходимость вычисления значения определённого интеграла
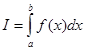
Как известно из курса математики, аналитически вычисление интеграла можно провести не во всех случаях. И даже в том случае, когда удаётся найти аналитический вид этого интеграла, процедура вычисления даёт приближённый результат, поэтому возникает задача приближенного значения этого интеграла.
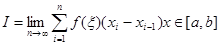
Суть приближенного вычисления заключается в двух операциях: 1. в выборе конечного числа вместо n; 2. в выборе точки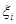 
в соответствующем отрезке.
В зависимости от выбора 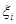мы получаем различные формулы для вычисления интеграла: Формулы левых и правых прямоугольников (5), (6)
(5)
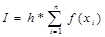(6)
Формула трапеции:
Формула Симпсона
где m=n/2
h=b-a/n
b, a - концы рассматриваемого отрезка.
Для сравнения результатов вычисления вышеизложенными формулами численного интегрирования вычислим 3-мя способами следующий интеграл, разделив отрезок [0, 
] на 6 равных отрезков:
|
|
h= 
По формуле левых прямоугольников:
По формуле трапеции:
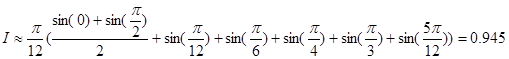
По формуле Симпсона:
А результат полученный аналитически равен
=1
Следовательно, можно сделать вывод о том, что численный метод интегрирования по формуле Симпсон является более точным, но используется в общем случае при делении рассориваемого отрезка на чётное число промежутков.
Квадратурные формулы
Формулы прямоугольников являются наиболее простыми квадратурными формулами. Разобьем отрезок интегрирования [ a, b ] на п равных частей длиной 
. Заметим, что величину h называют шагом интегрирования. В точках разбиения х 0 = а, х 1 = a + h,..., xn= b отметим ординаты y 0, y 1,…, yn кривой f (x), т.е. вычислим уi = f (xi), xi = a+ ih = xi -1 + h (i = 
). На каждом отрезке длиной h построим прямоугольник со сторонами h и yi, где i = , т.е. по значениям ординат, вычисленных в левых концах отрезков. Тогда площадь криволинейной трапеции, определяющую величину интеграла (1), приближенно можно представить в виде суммы площадей прямоугольников (рис. 1). Отсюда получим формулу прямоугольников:
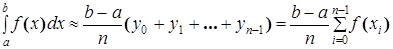. (3)
Если при вычислении интегральной суммы брать значения функции f (x) не в левых, а в правых концах отрезков длиной h, что показано на рис. 1 пунктирной линией, то получим второй вариант формулы прямоугольников:
. (4)
Третий вариант формулы прямоугольников можно получить при использовании значений функции f (x), вычисленных в средней точке каждого отрезка длины h (рис. 2):
. (5)
Формулы (3), (4) и (4) называют формулами левых, правых и центральных прямоугольников соответственно.
|
|
 |
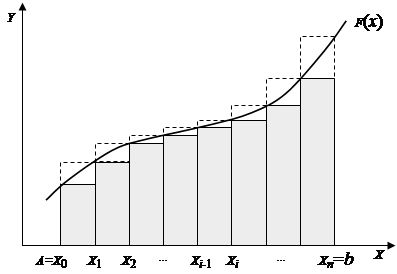Рис. 1
 |
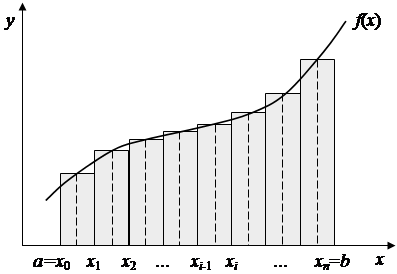Рис. 2
Формула трапеций. Здесь на каждом элементарном интервале [ xi -1, xi ] длины h точки с координатами (xi -1, yi -1) и (xi, yi) соединяются отрезком (рис. 3). Тогда площадь трапеции, построенной на этом интервале, определяется произведением 0,5 h (yi -1 + yi). Суммируя площади элементарных трапеций для i = 
получим приближенное значение интеграла:
. (6)
 |
Рис. 3.
Формула Симпсона. Разобьем интервал интегрирования на 2 n равных частей длиной 
. На каждом отрезке [ xi, xi+2 ] подынтегральную функцию f (х) заменим параболой, проходящей через точки (xi, yi), (xi +1, yi +1), (xi +2, yi +2). Тогда приближенное значение интеграла определяется формулой Симпсона:
. (7)
При вычислениях на ЭВМ более удобна следующая формула:
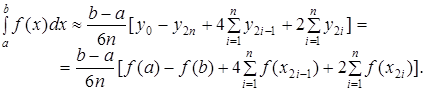
Метод Симпсона - один из наиболее широко известных и применяемых методов численного интегрирования, он дает точные значения интеграла при интегрировании многочленов до третьего порядка включительно.
Формула Ньютона. Приближенное значение интеграла по формуле Ньютона вычисляется следующим образом:
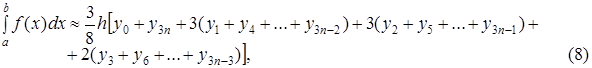
где число участков разбиения кратно трем, т.е. составляет 3 n. При разработке программ для ЭВМ удобнее использовать эквивалентную формулу:
Метод Ньютона дает точные значения интеграла при интегрировании многочленов до четвертого порядка включительно.