Определение случайной величины. Закон распределения.

Случайной величиной называется функция, определенная на пространстве элементарных исходов и принимающая действительные значения. Случайные величины будем обозначать большими буквами, а их значения - маленькими буквами латинского алфавита. Обозначим множество действительных чисел через R, а случайную величину через X. Тогда: X: ® R. Случайная величина должна удовлетворять еще одному условию. При любом действительном числе x Î R для события А_x = {wç X (w) < x } определена вероятность Р (А_x). Ведь согласно определению вероятности, она не обязана быть определена для любого события.

Случайная величина называется дискретной, если множество ее значений конечно или счетно, т.е. может быть представлено в виде бесконечной последовательности чисел . Каждое значение дискретная случайная величина принимает с определенной вероятностью. Заметим, что случайная величина Y принимает такие же значения с такими же вероятностями, но, тем не менее, случайные величины X и Y разные.

Законом распределения дискретной случайной величины называется взаимно однозначное соответствие между ее значениями x_i и вероятностями p_i, с которыми эти значения принимаются, где p_i = Р (X = x_i).Удобно соответствие между значениями и вероятностями дискретной случайной величины задавать в виде таблицы:где x₁ <x₂ <..., .Такая таблица называется рядом распределения дискретной случайной величины.

7.Биномиальное распределение. Рассмотрим подробнее несколько наиболее часто встречающихся дискретных случайных величин.

Случайная величина S_n имеет биномиальное распределение, если она означает количество появлений события А в n независимых опытах.Случайная величина S_n принимает целые неотрицательные значения 0, 1, 2,..., n с вероятностями Р_n (m), задаваемыми формулой Бернулли.

При больших значениях n вычисления вероятностей P_n (m) затруднительны. Если вероятность Р появления события А в одном опыте мала, то можно воспользоваться приближенной формулой

Применение этой формулы обосновывает следующая

Теорема. Если и так, что имеет пределом некоторое число l>0, то

при любых m = 0, 1, 2,....

Случайная величина ξ с таким распределением имеет смысл числа успехов в n испытаниях схемы Бернулли с вероятностью успеха р. Таблица распределения ξ имеет вид.

 

ξ	0	1	..	k	..	n
Р	(1-p)n	n p(1-p)n-1	..	Cnkpk (1-p)n-k	..	Pn

8.Распределение Пуассона. Геометрическое распределение. Случайная величина, принимающая целые неотрицательные значения m = 0, 1, 2,... с вероятностями

где l> 0, называется распределенной по закону Пуассона. Предположим, что серия независимых опытов проводится до тех пор, пока не появится событие А. Обозначим через Р - вероятность появления события А в одном опыте, а через X - количество проведенных опытов. Так определенная случайная величина X называется распределенной по геометрическому закону. Из независимости опытов сразу следует, что при m = 1, 2,.... Геометрическое распределение. Говорят, что случайная величина τ имеет геометрическое распределение с параметром р, где 0 £ p £, n, и пишут τ Î G _р, если τ принимает значения 1, 2, 3, … с вероятностями P(τ = k) = p (1-p)^k-1. Случайная величина τ с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха р.

9.Независимость случайных величин. Случайные величины называются независимыми, если для всех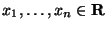

Другими словами, набор есть набор независимых событий.Случайные величины с абсолютно непрерывным распределением являются независимыми тогда и только тогда, когда

10.Математическое ожидание ДСВ, его смысл, свойства. Мат ожидание биномиального и геометрических законов, и закона Пуассона. Дадим теперь строгое определение математического ожидания дискретной случайной величины X, имеющий закон распределения P (X = x_i) = p_i. Если < ¥, то математическим ожиданием случайной величины X называют число . Если случайная величина Z является функцией случайных величин X и Y, т.е. Z = f (X, Y), то математическое ожидание M (Z) можно вычислить по формуле: где x_i пробегают все значения случайной величины X, а y_j - случайной величины Y. Рассмотрим свойства математического ожидания дискретной случайной величины. 1. Математическое ожидание постоянной равно этой постоянной, т.е. если С = const, то M ( C ) = C. Действительно, константу можно рассматривать как случайную величину, принимающую значение С с вероятностью 1. Поэтому M (C) = 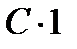= C. 2.Постоянную величину можно выносить за знак математического ожидания, т.е. M ( cX ) = cM ( X ). Согласно определению случайной величины cX, ее значения c x_i, а вероятности P (cX = cx_i) = P (X = x_i). Поэтому 3.Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых, т.е. M ( X + Y ) = M ( X ) + M ( Y ). Доказательство проведем лишь для случая, когда случайные величины X и Y имеют конечное множества значений и 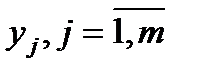, соответственно. При доказательстве будем использовать следующие равенства:

Действительно, события А₁ = { X = x₁ },..., А_n = { X = x_n } составляют полную группу событий. Если обозначить В_j = { Y = y_j }, то B_j = B_j = B_j 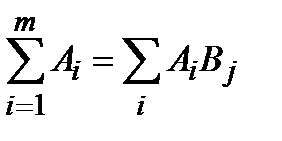. Поэтому т.е. Аналогично доказывается и первое равенство. Вычислим математическое ожидание случайной величины X + Y, обозначив ее значения через z_p:

где три последние суммы распространяются на всевозможные значения индексов i, j. Порядок суммирования можно выбрать произвольно. Следовательно,

n

4.Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей, т.е. M ( XY ) = M ( X )× M ( Y ). Как и в предшествующем случае доказательство проведем лишь для случайных величин, принимающих конечные множества значений:

n

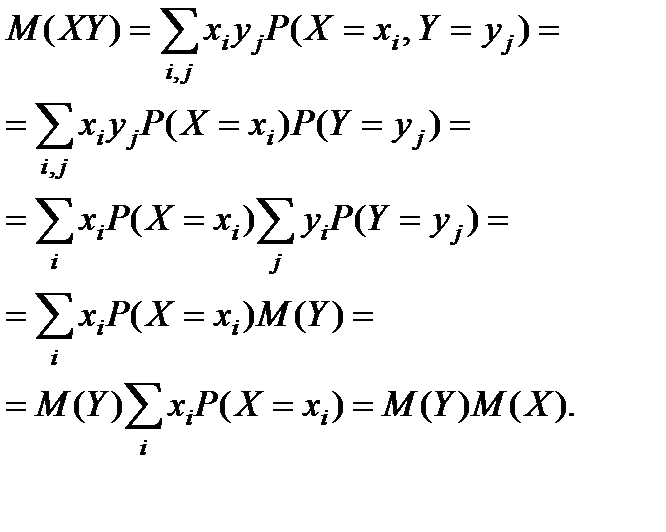Степень рассеивания случайной величины характеризуется дисперсией. Математическое ожидание и дисперсия случайной величины - ее основные числовые характеристики. Математическое ожидание дискретного распределения. Если X — дискретная случайная величина, имеющая распределение 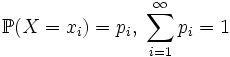, то прямо из определения интеграла Лебега следует, что 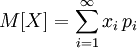. Математическое ожидание абсолютно непрерывной случайной величины, распределение которой задаётся плотностью f_X(x), равно 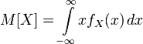Используя свойства математического ожидания, вычислим его для случайной величины, распределенной по биномиальному закону. M(S_n) = M(S_n⁽¹⁾ +... + S_n⁽ⁿ⁾) = M(S_n⁽¹⁾) +... + M(S_n⁽ⁿ⁾) = . математическое ожидание случайной величины, имеющей геометрическое распределение

 

Вычислим математическое ожидание случайной величины, распределенной по закону Пуассона m = 0, 1, 2,...; l > 0.

11.Дисперсией случайной величины X называется число D (X), определенное как математическое ожидание случайной величины Y = (X - M (X))², т.е. D (X) = M (X - M (X))². Если дискретная случайная величина X имеет распределение P (X = x_i) = p_i для i Î I, то D (X) = где m = M (X). В том случае, когда I - бесконечное множество, ряд (5) может расходиться. Тогда случайная величина X не имеет дисперсии. Величина называется среднеквадратическим отклонением случайной величины X. Заметим, что определение s_x корректно, т.к. D (X) . Для практического вычисления дисперсии удобно использовать формулу: D (X) = M (X ²) - M ²(X). Действительно, D (X) = M (X - m)² = M (X ² - 2 mX + m ²)= M (X ²) - 2 mM (X) + m ² = M (X ²) - 2 m ² + m ² = M (X ²) - m ². Используя свойства математического ожидания, выведенные для дискретных случайных величин, можно доказать следующие свойства дисперсии дискретной случайной величины. 1.Дисперсия постоянной равна нулю, т.е. D ( C ) = 0. Действительно, D (C) = M (C - M (C))² = M (C - C)² = M (0) = 0. 2. Постоянную можно выносить за знак дисперсии, возводя ее в квадрат, т.е. D (cX) = c ² D (X). D (cX) = M (cX - M (cX))² = M (cX - cM (X))² = M (c ²(X - m)²)= c ² M (X - m)² = c ² D (X). 3.Если X и Y независимые случайные величины, то D ( X + Y ) = D ( X ) + D ( Y ). ■ D (X + Y) = M (X + Y)² - M ²(X + Y) = = M (X ² + 2 XY + Y ²) - M ²(X) - 2 M (X) M (Y) - M ²(Y) = = M (X ²) + 2 M (XY) + M (Y ²) - M ²(X) - 2 M (X) M (Y) - M ²(Y).Так как случайные величины X и Y независимы, то M (XY) = M (X) M (Y). Поэтому D (X + Y) = M (X ²) - M ²(X) + M (Y ²) - M ²(Y) = D (X) + D (Y). ■ 4.Пусть X₁, X₂ ,..., X_n попарно независимые случайные величины. Тогда D (X₁ + X₂ +... + X_n) = D (X₁) + D (X₂) +... + D (X_n).■Действительно, D (X₁ + X₂ +... + X_n) = M (X₁ + X₂ +... + X_n - m₁ - m₂ -... - m_n)²,где m_i = M (X_i). Очевидно, что При i = j имеет M( (X_i - m_i)(X_j - m_j)) = D (X_i), а при i ¹ j M( (X_i - m_i)(X_j - m_j)) = M (X_i - m_i) M (X_j - m_j), т.к. случайные величины X_i - m_i и X_j - m_j в этом случае независимы. Но M (X_i - m_i) = M (X_j - m_j) = 0. Значит . Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения. По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула: Дисперсия случайной величины X, распределённой по биномиальному закону, D(X)=np

12. Функции распределения и ее свойства. Функция F (x) действительного аргумента x, определенная как вероятность события A_x = { w | X (w) < x } называется функцией распределения случайной величины X, т.е. F (x) = P (X < x).

Свойства: 1) значения функции распределения принадлежат отрезку [0, 1].

2) F(x) – неубывающая функция.

при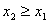

3) Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале.

4) На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице. 5) Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.Таким образом, не имеет смысла говорить о каком – либо конкретном значении случайной величины. Интерес представляет только вероятность попадания случайной величины в какой – либо интервал, что соответствует большинству практических задач.