Электромагнитная индукция

Установочные лекции по физике

Магнитное поле

· Магнитное поле создается движущимися зарядами или токами.

· Характеристики магнитного поля:

- вектор магнитной индукции, характеризует результирующее поле, создаваемое макро- и микротоками, [ B ] = 1 Тл (тесла),

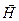- напряженность магнитного поля, характеризует поле, создаваемое макротоками, [ Н ] = 1 А/м.

Макроскопические токи – токи проводимости в проводниках, микроскопические токи – токи, обусловленные движением электронов в атомах.

· Магнитное поле называется однородным, если .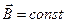

· Связь между В и Н: , где m ₀ = 4p×10^-7 Гн/м – магнитная постоянная, m – магнитная проницаемость среды (m = 1 для вакуума (воздуха), m < 1 для диамагнетиков, m > 1 для парамагнетиков, m >> 1 для ферромагнетиков).

· Магнитное поле изображают при помощи силовых линий (линий магнитной индукции) – касательная в каждой точке к которым совпадает с направлением вектора . Силовые линии магнитного поля замкнуты и охватывают проводники с током, их направление определяется правилом правого винта (буравчика): оно совпадает с направлением вращения головки винта при его поступательном перемещении вдоль тока.

· Магнитную индукцию dB, создаваемую элементом проводника dl, по которому течет ток силой I, на расстоянии r от dl можно определить по закону Био-Савара-Лапласа: . Модуль вектора магнитной индукции , а его направление определяется правилом правого винта (правилом буравчика).

· Для магнитного поля справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими зарядами или токами, равна векторной сумме магнитных индукций полей, создаваемых каждым из зарядов или токов: 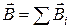или .

·

Правило буравчика

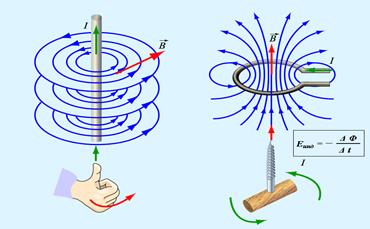Магнитная индукция B (напряженность H) поля, создаваемого бесконечным прямым проводником с током: 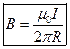, , 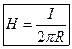где R – расстояние от оси проводника.

· Магнитная индукция (напряженность) в центре кругового проводника с током:

, , где R – радиус кругового проводника.

· Магнитная индукция (напряженность) поля внутри соленоида (тороида) в вакууме , , где n = N / l – число витков на единицу длины.

· На элемент длины проводника с током силой I в магнитном поле с индукцией действует сила Ампера: .

Модуль силы Ампера , где a - угол между векторами и . Для проводника конечной длины .

Направление силы 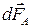определяется правилом левой руки: в ладонь , 4 пальца – по направлению тока, отогнутый на 90^о большой палец совпадает с направлением силы.

· Сила взаимодействия двух параллельных проводников длиной l с токами I ₁ и I ₂ , которые находятся на расстоянии d друг от друга

.

 

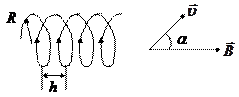· На заряженную частицу в магнитном поле действует сила Лоренца: , где q – заряд частицы, u – ее скорость, a – угол между векторами и . Модуль силы Лоренца .

o Если заряженная частица влетает в магнитное поле под углом a, она движется по винтовой линии.

– радиус окружности, 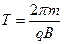– период обращения, – шаг винтовой линии.

· Для исследования магнитных полей используют контур с током, который характеризуется собственным магнитным моментом: , модуль которого , а его направление определяется правилом правого винта, I – сила тока, S – площадь контура, – вектор единичной нормали, [ p_m ] = 1 А×м².

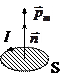· На контур с током в магнитном поле действует момент сил 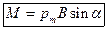, который поворачивает контур так, чтобы .

· Закон полного тока для магнитного поля в вакууме: циркуляция магнитной индукции в вакууме по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых этим контуром, умноженной на : .

Циркуляцией вектора называется криволинейный интеграл по замкнутому контуру (математическая процедура – суммирование вектора вдоль какого-то контура).

· Магнитный поток для однородного магнитного поля где, a – угол между В и нормалью к S, [F] = 1 Вб (вебер).

· Теорема Остроградского-Гаусса для поля вектора : Поток вектора сквозь любую замкнутую поверхность равен нулю: .

( - интеграл по замкнутой поверхности ). Эта теорема выражает факт, что в природе нет магнитных зарядов, на которых начинались бы и заканчивались линии магнитной индукции.

· Работа по перемещению проводника с током (контура с током) в магнитном поле: где, – изменение магнитного потока, сцепленного с контуром.

 

Электромагнитная индукция

· Закон Фарадея для электромагнитной индукции: Э.д.с. магнитной индукции, возникающая в замкнутом контуре, равна скорости изменения магнитного потока через поверхность, ограниченную этим контуром, взятой с обратным знаком. , где e_i – эдс индукции, F – магнитный поток. e_i = I_i×R (I_i = dq/dt – сила индукционного тока).

Знак минус указывает на направление индуктивного тока и является математическим выражением правила Ленца: направление индукционных токов таково, что создаваемое ими магнитное поле противодействует изменению магнитного потока вызвавшего индукционный ток (причине вызывающей эти токи), т.е. при , и наоборот.

· эдс индукции, возникающая в рамке, имеющей N витков площадью S, которая вращается в однородном магнитном поле с индукцией B с угловой скоростью w = 2 pn, где n – линейная частота,

, .

· разность потенциалов на концах проводника длиной l, который движется в магнитном поле с индукцией B со скоростью v .

· заряд q (количество электричества), прошедший через контур при изменении магнитного потока от Ф₁ до Ф₂ , где R – сопротивление контура.

· Возникновение эдс индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией.

· Индуктивность контура называется скалярная физическая величина L, равная отношению магнитного потока, сцепленного с контуром, к силе тока, протекающего по контуру и создающего этот магнитный поток: 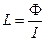, [ L ] = 1 Гн.

· индуктивность соленоида (тороида) (19), где объем V = lS, l – длина, S площадь поперечного сечения соленоида, n = N/l – число витков на единицу длины, N – число витков соленоида.

· Потокосцепление катушки (соленоида) (N – число витков соленоида, F – магнитный поток через один виток).

· эдс самоиндукции: .

· Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом или при изменении их взаимного расположения называется взаимной индукцией.

При изменении силы тока I ₁ в первом контуре, во втором контуре возникает э.д.с.: .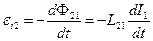

· Энергия магнитного поля: .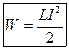

· Объемная плотность энергии однородного магнитного поля .

Уравнения Максвелла

Максвелл показал, что переменное электрическое поле создает вокруг себя переменное магнитное поле и наоборот. Таким образом, электрическое и магнитное поля неразрывно связаны друг с другом и образуют единое электромагнитное поле.

Уравнения Максвелла в интегральной форме:

1) (Переменное магнитное поле порождает вихревое электрическое поле.)

2) (Магнитное поле порождается переменным электрическим полем.)

3) (Источником электрического поля являются электрические заряды.)

4) . (Свободных магнитных «зарядов» в природе не существует.)

Эта система уравнений не является полной. Их необходимо дополнить тремя уравнениями, характеризующими электрические и магнитные свойства среды. В случае изотропной однородной среды: ..

Максвелл показал, что в вакууме электромагнитные возмущения распространяются со скоростью света:

.

Гармонические колебания

Колебаниями называются процессы, которые повторяются во времени.

Колебания называются свободными, если они совершаются за счет первоначально сообщенной энергии.

Гармонические колебания – колебания описываемые по закону синуса или косинуса:

· Уравнение гармонических колебаний 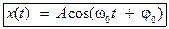, где x (t) – смещение точки от положения равновесия; А – амплитуда колебания – максимальное смещение (А = | x _max|).

w ₀ – собственная частота гармонического осциллятора – число колебаний за 2 p секунд, , [w] = 1 рад/с= 1 с^-1;

Т – период колебания – время одного полного колебания. [Т] = 1 с.

n – линейная частота – число колебаний за одну секунду , [n] = 1 Гц = 1 с^-1;

() – фаза колебания – характеризует мгновенное состояние колебательной системы, определяется смещением от положения равновесия и временем.

j ₀ – начальная фаза колебания – фаза колебания в момент времени t = 0.

· Скорость точки, совершающей гармонические колебания:

, где .

· Ускорение точки, совершающей гармонические колебания: 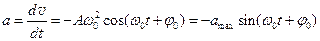, где .

· Полная механическая энергия точки, совершающей гармоническое колебание:

· Сложение колебаний:

а) одного направления: x ₁ = A ₁cos(w₀ t + j₀₁), x ₂ = A ₂cos(w₀ t + j₀₂), x = x ₁ + x _2.

Уравнение результирующего колебания: , где , Dj = j₀₂ – j₀₁; .

б ) взаимноперпендикулярных: x = A ₁cos(w₀ t + j₀₁), y = A ₂cos(w₀ t + j₀₂).

– уравнение траектории результирующего колебания – эллипс.

· Дифференциальное уравнение гармонических механических свободных незатухающих колебаний: , его решение: .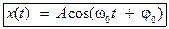

· Примеры гармонических осцилляторов

а) пружинный маятник: , (9);
б) математический маятник: ,
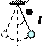
в) физический маятник , (11);
I – момент инерции относительно точки подвеса, m – масса маятника, d – расстояние от точки подвеса до центра масс.

г) колебательный контур – (12). L – индуктивность, C – емкость.

· Дифференциальное уравнение гармонических электромагнитных свободных незатухающих колебаний , его решение q = q _mcos(w₀ t + j₀), где q – заряд на обкладках конденсатора.

U = U _mcos(w₀ t + j₀) – напряжение на конденсаторе, U _m = q _m/C,

I = – I _msin(w₀ t + j₀) – ток в контуре, I _m = q _mw.

· Полная энергия электрического поля:

.

 

Затухающие колебания

· Дифференциальное уравнение свободных затухающих колебаний:

, его решение: - уравнение затухающих колебаний, где –амплитуда затухающих колебаний, – условная частота затухающих колебаний, b – коэффициент затухания, , где r – коэффициент сопротивления среды, m – масса тела.

· Энергия затухающих колебаний: .

· Декремент затухания 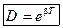– показывает, во сколько раз амплитуда колебаний уменьшается за период колебаний.

– логарифмический декремент.

Добротность – показывает убыль энергии через один период: 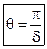– добротность.