Глава YI. Линейные пространства.
Из курса векторной алгебры известно, что свободные векторы на плоскости (и в пространстве) можно складывать и умножать на вещественные числа, причём эти операции обладают определёнными свойствами.
Многочлены с вещественными (комплексными) коэффициентами также можно складывать и умножать на вещественные (комплексные) числа, причём и эти операции обладают аналогичными свойствами.
В этой главе мы будем изучать множества элементов произвольной природы, для которых определены операции сложения и умножения на числа, причём эти операции обладают теми же свойствами, что и соответствующие операции над свободными векторами.
Такие множества обладают рядом общих свойств и называются линейными пространствами.
Понятие линейного пространства.
Определение поля.
Полем будемназывать множество K элементов произвольной природы, для которого выполнены следующие три требования:
I. На множестве K определена операциясложения, т.е. имеется правило, с помощью которого любой упорядоченной паре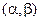 
элементов этого множества ставится в соответствие единственный элемент 
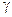этого множества, называемый их суммой, который будем обозначать так: 
.
II. На множестве K определена операцияумножения, т.е. имеется правило, с помощью которого любой упорядоченной паре 
элементов этого множества ставится в соответствие единственный элемент 
этого множества, называемый их произведением, который будем обозначать так: 
.
III. Эти операции подчиняются следующим 9 аксиомам:
1.Коммутативность сложения. Для любых элементов 
K справедливо равенство:
2. Ассоциативность сложения. Для любых элементов 
K справедливо равенство:
3. Существование нулевого элемента. Среди элементов множества K существует элемент, обозначаемый так: 0 и называемый нулевым, такой, что для любого элемента 
K справедливо равенство:
4. Существование противоположного элемента. Для любого элемента K существует элемент множества K, обозначаемый так: 
и называемый противоположным к 
, и такой, что справедливо равенство:
5. Коммутативность умножения. Для любых элементов K справедливо равенство:
6.Ассоциативность умножения. Для любых элементов K справедливо равенство:
7. Дистрибутивность. Для любых элементов K справедливо равенство:
8. Существование единицы. Среди элементов множества K существует элемент, обозначаемый так: 1 и называемый единицей, такой, что для любого элемента K справедливо равенство:
9. Существование обратного элемента. Для любого элемента K, не равного нулевому, существует элемент, обозначаемый так: 
и называемый обратным к , и такой, что справедливо равенство:
Замечание 1. Элементы поля в дальнейшем будем называть числами.
Пример 1. Множество вещественных чисел R, очевидно, является полем.
Пример 2. Множество комплексных чисел C, очевидно, является полем.
Пример 3. Множество рациональных чисел Q, очевидно, является полем. Напомним, что рациональное число - это такое, которое можно представить в виде 
, где 
и 
- целые числа.
Пример 4. Множество Q 
Q 
также является полем. Докажите это утверждение.
Пример 5. Множество Z, состоящееизвсех целых чисел, не является полем, т.к. не выполняется аксиома 9.
Например, для числа 2 нет обратного, т.е. такого целого числа , чтобы выполнялось равенство 
.
Пример 6. Множество K 
всех квадратных матриц вида 
, где 
R является полем.
На этом множестве определены операции сложения и умножения. Очевидно, нулевым элементом является нулевая матрица 
, которая принадлежит K . Единичная матрица 
, которая также принадлежит K , исполняет роль единицы. Действительно, ранее было доказано, что для любой квадратной матрицы 
второго порядка справедливы равенства 
и 
. В частности, эти равенства выполняются и для матриц из множества K . Кроме того,для любой матрицы 
противоположной служит матрица 
K . Следовательно, аксиома 4 также выполнена. Остальные аксиомы, за исключением 5-ой, и 9-ой выполняются для всех квадратных матриц второго порядка, в частности, эти аксиомы выполняются и для матриц из множества K .
Покажем, что на множестве K умножение коммутативно. Вычислим
и
для любых матриц 
K .
Покажем, что для любой ненулевой матрицы 
K существует обратная матрица, принадлежащая K . Действительно, матрица 
K . Таким образом, множество K относительно обычных операций сложения и умножения матриц является полем.
Пример 7. Пусть множество Z 
состоит из двух элементов, которые будем обозначать так: 1 и 0.
Операцию сложения на этом множестве зададим так: 
.
Операцию умножения на этом множестве зададим так: 
.
Легко проверить, что множество Z является полем, которое называют полем из двух элементов. Заметим, что существуют и другие поля, содержащие конечное число элементов.
Замечание 2. Для матриц одинакового строения с элементами из поля K определена операция сложения (см. глава III§2).
Замечание 3. Для матриц с элементами из поля K определена операция умножения на числа, т.е. элементы поля K. Для этих операций сложения матриц и умножения их на числа поля K справедливы 8 свойств (см. глава III§2).
Замечание 4. Для матриц с элементами из поля K согласованного строения определена операция умножения, причём эта операция удовлетворяет 6 свойствам (см. глава III§3).
Справедливость этих утверждений предлагается проверить самостоятельно в качестве упражнения. В дальнейшем мы будем пользоваться этими утверждениями.
Определение линейного пространства.
Множество X элементов произвольной природы будемназывать линейным пространством над полем
K, если для него выполнены следующие три требования:
I. На множестве X определена операциясложения, т.е. имеется правило, с помощью которого любой упорядоченной паре 
элементов этого множества ставится в соответствие единственный элемент 
этого множества, называемый их суммой, который будем обозначать так: 
.
II. На множестве X определена операцияумножения на числа, т.е. на элементы поля K. Это означает, что имеется правило, с помощью которого любому числу 
K и любому элементу 
X ставится в соответствие единственный элемент 
множества X, называемый их произведением, который будем обозначать так: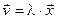 
или так: 
.
III. Эти операции подчиняются следующим 8 аксиомам:
1.Коммутативность сложения. Для любых элементов 
X, справедливо равенство:
2. Ассоциативность сложения. Для любых элементов 
X, справедливо равенство:
3. Существование нулевого элемента. Среди элементов множества X существует элемент, обозначаемый так: 
и называемый нулевым, такой, что для любого элемента X, справедливо равенство:
4. Существование противоположного элемента. Для любого элемента X, существует элемент множества X, обозначаемый так: 
и называемый противоположным к 
, и такой, что справедливо равенство:
5. Для любого элемента X, справедливо равенство:
, где 
- единица поля K.
6. Дистрибутивность относительно сложения векторов. Для любых элементов X, и для любого числа K справедливо равенство:
7. Дистрибутивность относительно сложения чисел. Для любых чисел K и длялюбого элемента X справедливо равенство:
8. Для любых чисел K идля любого элемента X справедливо равенство:
Замечание 1. Линейное пространство над полем K называют также векторным пространством над полем K.
Если по смыслу ясно, о каком поле идёт речь, или неважно каково поле K, то иногда X будем называть просто линейным пространством.
Замечание 2. Элементы линейного пространства будем, как правило, обозначать маленькими буквами латинского алфавита, снабжёнными сверху стрелкой, и называть векторами. Элементы поля K, т.е. числа, будем обозначать греческими буквами. Разумеется, будут и отступления от этих договорённостей.
Пример 1. Из курса векторной алгебры известно, что множества V и V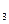 
свободных векторов на плоскости и в пространстве соответственно, являются линейными пространствами над полем вещественных чисел относительно имеющихся там операций сложения и умножения на вещественное число.
Пример 2. Из свойств действий над матрицами следует, что X = 
(K) является линейным пространством над полем K относительно имеющихся там операций сложения и умножения на числа поля K. В частности,множества K 
, K 
, 
(K) являются линейными пространствами над полем K относительно имеющихся там операций сложения и умножения на числа поля K.
Пример 3. Множество X = R 
всех многочленов от буквы 
с вещественными коэффициентами является вещественным линейным пространством (или линейным пространством над полем R).
Пример 4. Множество X 
непрерывных на отрезке 
функций является вещественным линейным пространством, если сложение и умножение на вещественные числа определить так:
для любого 
;
для любого и любого R.
Пример 5. Множество X = R всех многочленов от буквы с вещественными коэффициентами степени не превосходящей , является вещественным линейным пространством (или линейным пространством над полем R).
Замечание 3. Определение умножения матриц будем использовать и в случае, когда их строение согласовано известным образом (см. глава III§3), причём элементами одной матрицы являются векторы линейного пространства X над полем K, а элементами другой матрицы – числа, т.е. элементы поля K.
В качестве упражнения предлагается доказать, что и в этом случае для умножения матриц справедливы 6 свойств (см. глава III§3).