Лекция 3. Рациональные дроби.
Содержание лекции: Рациональные дроби, правильные, неправильные. Простейшие рациональные дроби. Представление правильной рациональной дроби в виде суммы простейших. Метод неопределенных коэффициентов.
В этой лекции мы будем рассматривать многочлены только на множестве действительных чисел, а переменную будем обозначать х.
Определение 3.1.
Рациональной дробью называется отношение двух многочленов:
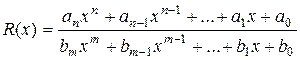 ,
,
Если  (степень числителя меньше степени знаменателя), то дробь называется правильной; если
(степень числителя меньше степени знаменателя), то дробь называется правильной; если  (степень числителя не меньше степени знаменателя), то дробь называется неправильной.
(степень числителя не меньше степени знаменателя), то дробь называется неправильной.
Например, 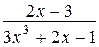 - правильная дробь (степень многочлена, стоящего в числителе, равна 1, а степень многочлена-знаменателя равна 3). Дроби
- правильная дробь (степень многочлена, стоящего в числителе, равна 1, а степень многочлена-знаменателя равна 3). Дроби  и
и  – неправильные.
– неправильные.
Если  =
=  – неправильная дробь, то, выполнив деление многочлена Р (х) на многочлен Q (x):
– неправильная дробь, то, выполнив деление многочлена Р (х) на многочлен Q (x):
P(х) = Q(х)S(х) + R(х),
можно представить эту дробь в виде суммы
 = S(x) +
= S(x) +  ,
,
где S(x) – многочлен, а  – правильная рациональная дробь. Многочлен S(x) называют целой частью неправильной рациональной дроби.
– правильная рациональная дробь. Многочлен S(x) называют целой частью неправильной рациональной дроби.
Правильные дроби вида:
I.  II.
II. 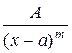 III.
III. 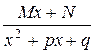 IV.
IV. 
называются простейшими или элементарными. Здесь А, M, N, a, p, q – действительные числа, т ³ 2 – натуральное число, квадратный трехчлен  – неприводимый многочлен (дискриминант D = p 2 – 4 q < 0).
– неприводимый многочлен (дискриминант D = p 2 – 4 q < 0).
Теорема 3.1
Всякую правильную рациональную дробь можно представить в виде суммы простейших дробей (разложить на простейшие дроби). При этом если знаменатель правильной дроби представлен в виде произведения неприводимых множителей
 ,
,
то
· каждому множителю вида  в указанной сумме соответствует дробь вида
в указанной сумме соответствует дробь вида  ;
;
· каждому множителю вида  в разложении соответствует сумма т дробей
в разложении соответствует сумма т дробей  ;
;
· множителю вида  в разложении соответствует дробь вида
в разложении соответствует дробь вида 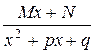 ;
;
· множителю вида  соответствует сумма дробей
соответствует сумма дробей

Например,  =
=  +
+  ,
,
 =
= 
Тогда всякую неправильную рациональную дробь можно представит в виде суммы целой части и простейших рациональных дробей. Для этого выделяют целую часть дроби, разделив числитель на знаменатель, а затем полученную правильную рациональную дробь разлагают на сумму простейших.
Разложение правильных дробей на простейшие можно проводить, придерживаясь следующего алгоритма:
Алгоритм разложения правильной дроби  :
:
1. Знаменатель правильной рациональной дроби разложить на неприводимые множители (если при разложении получим квадратный трехчлен, имеющий иррациональные корни, то будем считать его неприводимым).
2. Учитывая теорему 3.1, составить сумму простейших дробей с неопределенными коэффициентами, записав для каждого неприводимого множителя знаменателя соответствующую ему одну или несколько простейших дробей.
3. Найти коэффициенты разложения.
4. Подставить найденные значения коэффициентов в составленную формально сумму и записать окончательное разложение.
Неизвестные коэффициенты разложения можно находить следующими способами.
Метод неопределённых коэффициентов.
Составленную формально сумму простейших дробей (с неизвестными, буквенными, коэффициентами) привести к общему знаменателю (этот общий знаменатель обязательно равен знаменателю исходной дроби) и сложить дроби. Записать равенство числителей исходной и вновь полученной дробей. Приравняв коэффициенты при одинаковых степенях многочленов, стоящих в левой и правой частях этого равенства, записать систему уравнений относительно неизвестных коэффициентов разложения. Решив полученную систему уравнений, найти значения коэффициентов разложения и подставить их в разложение.
Метод частных значений.
Составленную формально сумму простейших дробей привести к общему знаменателю и сложить дроби. Записать равенство числителей исходной и вновь полученной дробей. В этом равенстве переменной придать числовые значения и записать систему уравнений относительно неизвестных коэффициентов разложения. Значений переменной нужно взять столько, сколько неизвестных коэффициентов в разложении дроби.В частности удобно придавать переменной х значения корней знаменатель исходной дроби.. Из полученной системы равенств найти неизвестные коэффициенты разложения и подставить их в разложение дроби.
Эти методы можно применять и в комбинации.
Пример 1: Разложить дробь  в сумму простейших.
в сумму простейших.
Запишем сначала формальное разложение
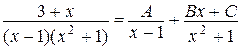 .
.
Теперь полученную сумму дробей приведем к общему знаменателю
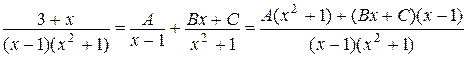
Приравняем числители полученной и исходной дробей:
3 + x = Ax 2 + A+Bx 2 + Cx – Bx – C, или (A+B) x 2 + (C-B) x + A – C =3 + x.
Два многочлена равны, если равны их коэффициенты при одинаковых степенях переменной:

Следовательно,  .
.
Пример 2: Разложить дробь  в сумму простейших.
в сумму простейших.
Действуем аналогично примеру 1:
 =
=
= 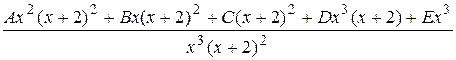

Придадим переменной х значения и сравним левую и правую части этого равенства:

Получили систему

Решив эту систему, находим

Тогда искомое разложение имеет вид
 .
.