Способы задания множества.
1.Перечисление: А={1,2,3,4,5};В={1,2,..,99}
2.С помощью характеристического свойства – свойства, которым обладает любой элемент входящий в множество и не обладает элемент не входящий в множество: А={а|P(a)}; B={k|k-чётное число}
3.Указанием порождающей процедуры.
Порождающая процедура – это процесс будучи запущен порождает все элементы данного множества. К={к|к=5n  -3n-2, где n
-3n-2, где n  N}.
N}.
Перечислением можно задать только конечные множества.
Диаграмма Эйлера-Венна.
Для наглядного изображения множеств и их свойств используют диаграммы, при этом множества мыслятся как множество точек круга.
Универсальное множество:- содержит в себе как подмножества все другие множества (V), принято изображать прямоугольником либо множеством.
.y
С В С  В
В
.x х  А
А
y  В
В
2) Операции над множествами и их свойства.
1.Объеденение (сумма) А и В - А  В называется множество состоящие из тех и только тех элементов принадлежащих хотя бы одному из множеств А или В.
В называется множество состоящие из тех и только тех элементов принадлежащих хотя бы одному из множеств А или В.
Опр: А  В={х|х
В={х|х  А или х
А или х  В}
В}
2.Пересечение (произведение) А и В - А  В состоит из элементов принадлежащих и А и В
В состоит из элементов принадлежащих и А и В
3.Разностью множеств А и В называется множества А\В состоящие из тех и только тех элементов которые принадлежат А и не принадлежат В.
А\В={х| х  А и х
А и х  В }=А
В }=А 

Частный случай разности: если А  V, V\A=
V, V\A=  ={x|x
={x|x  А}является дополнением множества А.
А}является дополнением множества А.
4.Симетрическая разность (кольцевая сумма) А и В называется множество А 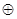 В (А
В (А  В) состоящие из элементов объединения этих множеств, но не входящие в пересечение этих множеств.
В) состоящие из элементов объединения этих множеств, но не входящие в пересечение этих множеств.
А 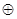 В=(А
В=(А  В)\(А
В)\(А  В)=(А\В)
В)=(А\В)  (В\А)={x| (х
(В\А)={x| (х  А и х
А и х  В) или (х
В) или (х  В и х
В и х  А)}
А)}
5.Декартовое произведение (прямое) множеств А и В называется множества АхВ состоящие из всех упорядоченных пар(а,в) где а  А и в
А и в  В.
В.
АхВ={(а,в)| а  А,в
А,в  В }
В }
Свойства операций над множествами.
1.Комутативность
А  В=В
В=В  А;В
А;В  А=А
А=А  В
В
2.Ассоциативность
(А  В)
В)  С=А
С=А  (В
(В  С);(А
С);(А  В)
В)  С=А
С=А  (В
(В  С)
С)
3.Дистрибутивность
А  (В
(В  С)=(А
С)=(А  В)
В)  (А
(А  С);А
С);А  (В
(В  С)=(А
С)=(А  В)
В)  (А
(А  С)
С)
4.Правило иденпотентности
А  А=А;А
А=А;А  А=А; А
А=А; А 
 =А; А
=А; А 
 =
=  ;А
;А  V=
V=  ;A
;A  V=A
V=A
5.Закон поглащение
А  (А
(А  В)=А;А
В)=А;А  (А
(А  В)=А
В)=А
6.Закон де`Моргана
 =
= 

 ;
;  =
= 


7.Закон двойного дополнения (инвалютивность)
 =А
=А
8.Закон включение
А  В
В 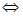



9.Закон равенства
А=В 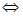 ((А
((А  В)
В)  (В
(В  А))
А)) 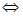 (А
(А  В)
В)  (
(

 )
)
10.Свойства дополнения
А 
 =V; А
=V; А 
 =
= 
3) Бинарные отношения.
Опр: n-местным отношением (предикатом Р) на множествах А  А
А  …А
…А 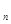 называется любое подмножество девартового произведения А
называется любое подмножество девартового произведения А  х А
х А  х…хА
х…хА 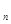 .
.
Если: n=1,то P называется унарным и Р(х  )
)  А
А 
n=2, то Р называется бинарным и это множество упорядоченных пар Р(х  х
х  )
)  А
А  х А
х А  ,
,
х 
 А
А  х
х 
 А
А 
опр: х  …х
…х  называются координатами или компонентами отношения Р
называются координатами или компонентами отношения Р
опр:  А отношение id
А отношение id  ={(х,х)/х
={(х,х)/х  А} называется тождественным отношением
А} называется тождественным отношением
V  =А
=А  =АхА={(x,y)/ х
=АхА={(x,y)/ х  А, y
А, y  А } называется полным отношением или квадратом.
А } называется полным отношением или квадратом.
Пусть Р это бинарное отношение множеств А  и А
и А  т.е Р
т.е Р  А
А  хА
хА 
Опр: областью определения бинарного отношения Р называется множество D=Dom Р={х/  y: (x.y)
y: (x.y)  Р}. Областью значений бинарного отношения Р называется множество R=Уm P= {х/
Р}. Областью значений бинарного отношения Р называется множество R=Уm P= {х/  x: (x.y)
x: (x.y)  Р}. Бинарные отношения R и S называются равными (R=S), если (x,y)
Р}. Бинарные отношения R и S называются равными (R=S), если (x,y)  R
R 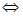 (x,y)
(x,y)  S т.е когда отношения R и S равны как множества. Если имеется запись, что (x,y)
S т.е когда отношения R и S равны как множества. Если имеется запись, что (x,y)  Р, то говорят что элементы x,y связаны отношением Р или что х находится в отношении Р с y или что для x и y выполняется отношение Р. (x,y)
Р, то говорят что элементы x,y связаны отношением Р или что х находится в отношении Р с y или что для x и y выполняется отношение Р. (x,y)  Р
Р 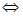 хРy
хРy
Способы задание бинарных отношений.
1.Перечесление. Применим только для конечных множеств
2.Характерестическое свойство
3.Диаграммой
4.Графом (если А=И то диаграмма становиться графом). Р ставим в соответствие след.геом.фигуру: точки явл.Dom Р, Уm P, а ориентированные рёбра (линии) т.е (а,в)  Р поставим в соответствие ореинтированное ребро идущее от А к В (А
Р поставим в соответствие ореинтированное ребро идущее от А к В (А  В) с фиксированным направлением входа. Такую фигуру будем называть ориентированным графом отношения Р каждому бинарному отношению Р на конечном множестве можно поставить в соответствие ориентированный граф и наоборот.
В) с фиксированным направлением входа. Такую фигуру будем называть ориентированным графом отношения Р каждому бинарному отношению Р на конечном множестве можно поставить в соответствие ориентированный граф и наоборот.
 Р={(а,в),(в,с),(d,d),(e,a),(e,e),(в,d)}
Р={(а,в),(в,с),(d,d),(e,a),(e,e),(в,d)}
в
с
а d
е
5.Графиком (этот способ применим если отношения задано на числовых множествах)
Графиком Р называется множество всех точек плоскости Оху с координатами (х,y)  Р
Р
Пример:


 Р={(x,y)/x,y
Р={(x,y)/x,y  R,y=х
R,y=х  }
}
6.Таблицей (для конечных множеств)
7.Матрицей(рассм. Конечное множество А)
А={(а  …а
…а 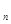 )}, В={в
)}, В={в  ,в
,в  …в
…в  }; Р
}; Р  АхВ –б.о
АхВ –б.о
||Р|| матрицей б.о Р называется ||Р||=(Р 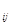 ) размера n x m, n=|A|, m=|B|
) размера n x m, n=|A|, m=|B|
1, если (а  ,в
,в  )
)  Р
Р
Р 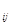 ={
={
0, если (а  ,в
,в  )
)  Р
Р
4) Операции над отношениями.
Опр: обратным к Р отношением (инверсия) называется Р 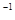 ={(y,x)/(x,y)
={(y,x)/(x,y)  Р} таким образом опр. унарную операцию перехода к обратному отн.
Р} таким образом опр. унарную операцию перехода к обратному отн.
Композицией (суперпозицией) б.о Р  АхВ и Q
АхВ и Q  BxC называется множество P
BxC называется множество P  Q={(x,y)/x
Q={(x,y)/x  A, y
A, y  C,
C,  z
z  В: (x,z)
В: (x,z)  P,(z,y)
P,(z,y)  Q}
Q}
Для любых б.о выполняется следующие свойства:
1.(Р 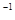 )
) 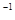 =Р
=Р
2.(P  Q)
Q) 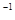 =Q
=Q 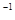
 Р
Р 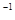
3..(P  Q)
Q)  R=P
R=P  (Q
(Q  R)
R)
Св-ва б.о на множестве.
Пусть отношение R задано на не пустом множестве А R  A
A 
1.Рефлексивность: б.о называется рефлексивным на А, если  х
х  А, (x,x)
А, (x,x)  R
R
R рефлексивно 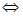 каждая вершина графа имеет петлю
каждая вершина графа имеет петлю
2.Антирефлексивность: б.о R на А называется антирефлексивным, если  х
х  А, (x,x)
А, (x,x)  R
R
R антирефлексивно 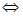 когда каждая вершина не содержит петли
когда каждая вершина не содержит петли
3.Симметричность: б.о R на А называется симметричным, если для  х,y
х,y  А, (x,y)
А, (x,y)  R
R  (y,x)
(y,x)  R. R симметрично
R. R симметрично 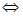 когда вместе с каждым ребром (х,y) граф содержит ребро (y,x)
когда вместе с каждым ребром (х,y) граф содержит ребро (y,x)
4.Антисемметричность: б.о R на А называеться антисемметричным, если  х,y
х,y  А (x,y)
А (x,y)  R и (y,x)
R и (y,x)  R
R  х=y.
х=y.
R-антисимметричноóдве различные вершины графа если соединены ребром, то только 1 при этом в графе могут быть петли
1)отношение делемости на множестве R
а:в и в:а  а=в
а=в
2)Отношение включения на любом подмножестве унивесального подмножества является антисемметр. А  В и В
В и В  А
А  А=В
А=В
5.Асиметричность: б.о является ассеметричным на А если для каждой пары элементов х и у из множества А одновременное выполнение отношений (х,у)  R и (у,х)
R и (у,х)  R не возможно т.е
R не возможно т.е  х,у
х,у  А если (х,у)
А если (х,у)  R,то (у,х)
R,то (у,х)  R.R асемметрично
R.R асемметрично 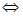 если граф содержит ребро (х,у), то он не содержит ребра (у,х)
если граф содержит ребро (х,у), то он не содержит ребра (у,х)
6.Транзитивность: б.о называется транзитивным на А если  х,у,z
х,у,z  R если (x,y)
R если (x,y)  Rи (y,z)
Rи (y,z)  Rто (x,z)
Rто (x,z)  R
R
R транзит. 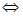 когда граф вместе с каждой парой посл.рёбер (х,у),(у,z) сод. Рубро замыкающее (х,z)
когда граф вместе с каждой парой посл.рёбер (х,у),(у,z) сод. Рубро замыкающее (х,z)
7.Связность: б.о называется связным на А, если  х,у
х,у  А: х
А: х  у либо (х,у)
у либо (х,у)  R либо (у,х)
R либо (у,х)  R. R связно
R. R связно 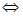 когда любые 2 вершины графа соеденены одним и только одним ребром.
когда любые 2 вершины графа соеденены одним и только одним ребром.
1)”>” на R связно;  на R несвязно
на R несвязно
5) Матричное представление бинарных отношений. Свойства матрицы бинарных отношений.
Бинарное отношение можно задать с помощью матрицы
Рассмотрим конечное множество A и B
A={a1,a2,…,an}, B={b1,b2,…,bn}
P⊆AxB, P – бинарное отношение
Опр: Матрицей бинарного отношения P называется матрица ||P||=(pij) размерности n x m, где n=|A|, m=|B|

Эта матрица содержит полную информацию о связи между элементами множеств A и B и позволяет представить эту информацию в графическом виде.
Заметим, что любая матрица, состоящая из 0 и 1 является матрицей некоторого бинарного отношения