1. Cnk = Cnn-k. Коэфф членов равноудаленных от начала и от конца разложения равны между собой. Соотношение симметрии

2. 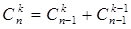 - формула сложения
- формула сложения
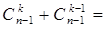


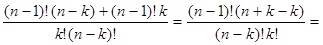
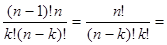

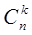
3. 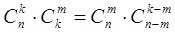
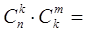


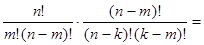
 4.
4. 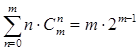 5.
5. 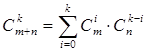 - тождество Коши
- тождество Коши
Треугольник Паскаля.
С помощью свойства 2 можно последоват вычислить 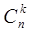 , используя кроме указ соответствия, след:
, используя кроме указ соответствия, след: 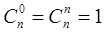 . Вычисляемые коэфф распол в виде таблицы, кот наз треугольником Паскаля или арифметич треугольником.
. Вычисляемые коэфф распол в виде таблицы, кот наз треугольником Паскаля или арифметич треугольником.
Полиномиальная теорема.
Обобщение формулы Ньютона на случ k-слагаемых 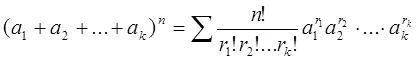 , где r1+r2+rk=n,
, где r1+r2+rk=n, 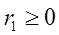 ,…,
,…, 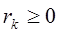 . Где суммирование производ по всем решениям ур r1+r2+…+rk=n в целых неотриц числах.
. Где суммирование производ по всем решениям ур r1+r2+…+rk=n в целых неотриц числах.
11) Конечные и бесконечные мн-ва. Равномощность. Счетные и не счетные мн-ва.
Опр Мн-ва A и B наз. Изоморфными (эквивалентными) A 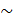 B, если
B, если  биекция f: A
биекция f: A 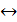 B. Биекция осуществляет взаимно-однозначное соответствие между элементами мн-в А и В. Отношение изоморфизма на любой совокупности множеств является отношением эквивалентности т.е.
B. Биекция осуществляет взаимно-однозначное соответствие между элементами мн-в А и В. Отношение изоморфизма на любой совокупности множеств является отношением эквивалентности т.е.
1.) Рефлексивность A  А т.к
А т.к 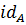 : A
: A 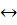 A – биекция
A – биекция
2.) Симметричность A  B, то В
B, то В  А, т.к A
А, т.к A  B => биекция
B => биекция 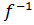 : B
: B 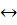 A
A
3.) Транзитивность Если A  B => f: A
B => f: A 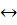 B и В
B и В  С => g: B
С => g: B 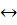 C, то A
C, то A  С
С
Биект. – f°g: A 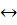 C => A
C => A  С
С
Кол-во элементов мн-ва наз. Мощностью множества или кардинальным числом
Опр А и В наз. Равномощными, если  биекция A
биекция A  B, т.е. мн-ва А и В равномощны, если они изоморфны
B, т.е. мн-ва А и В равномощны, если они изоморфны
Опр Мн-во наз. Конечным, если оно не равномощно ни одному собственному подмножеству
(рассмотреть натуральные и четные, соотнести их, они равномощны)
Опр Бесконечным мн-вом наз. Мн-во из которого можно выделить равномощное ему собственное подмножество
Опр Кардинальное число наз. Конечным (бесконечным), если оно явл. Мощностью конечного (бесконечного) мн-ва
Мн-во равномощно мн-ву N (мн-ву натуральных чисел) наз счетным, если его эл-ты можно пронумеровать
{ 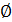 } – по опр. Относится к счетным мн-вам
} – по опр. Относится к счетным мн-вам
(доказательство что Q счетно, что R несчетно)
Мощность R (действительных) чисел =  наз. Мощностью континуума, если А
наз. Мощностью континуума, если А 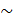 R или |A|=|R|=
R или |A|=|R|=  , то А назыв. Континуальным.
, то А назыв. Континуальным.
Т1. Всякое подмн-во счетного мн-ва конечно или счетно.
Т2. Объединение счетного числа счетных мн-в – счетно
Т3. Всякое бесконечное мн-во А – содержит счетное мн-во B:A\B – счетное мн-во
Т4. Всякое бесконечное мн-во А 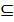 В равномощное А (A
В равномощное А (A 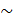 B), причем А\В – бесконечное мн-во
B), причем А\В – бесконечное мн-во
Т5. Теорема Кантора-Бернштейна
Если для двух мн-в А и В каждая изоморфна части другого, то эти мн-ва изоморфны между собой |A|≤|B|, |B|≤|A| => |A|=|B|
Т6. Мн-во всех подмн-в в произвольном мн-ве А 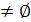 имеет мощность большую, чем мощность мн-ва А.
имеет мощность большую, чем мощность мн-ва А. 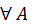 |P(A)|. Эта теорема верна и для
|P(A)|. Эта теорема верна и для 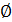 .
.
Мн-во всех подмножеств имеет вид Р(А) = { 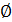 } т.е. =>
} т.е. =>  =>
=> 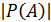 > |A|
> |A|
T7.  |P(A)|=
|P(A)|= 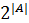
|A| = 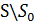 => |P(A)|=
=> |P(A)|= 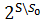 =>|P(A)|>|A|=>
=>|P(A)|>|A|=>  >
> 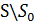
12) Алгебраические операции. Св-ва б.а.о.
Опр Бинарной алгебраической операцией на мн-ве А наз. Отображение f:(Dom f=A 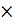 A) A
A) A 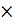 A
A  A
A
Для которого справедливо следующее: a,b 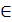 A
A 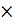 A
A  ! c
! c 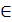 A: (a,b)
A: (a,b) 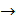 c; (f(a,b,)=c)
c; (f(a,b,)=c)
Опр n-местной алг. Операцией на мн-ве А наз f: из 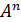
 A т.е. Dom f ⊆
A т.е. Dom f ⊆ 
Нуль-арные операции отличают некоторый элемент из множества А
Опр. Частичный n-местной алгебраической операцией на множестве А называется отображение f:A^n->A если область определения отображения f не совпадает с множеством A^n, т.е. Domf c A^n
На множестве А может быть задано много ращзличных операций. Если нужно выделить одну из них то используют скобки (А,*)
Говорят что операция * определяет на множестве А алгебраическую структуру или что (А,*) – алгебраическая структура (алгебраическая система)
Св-ва б.а.о.
1.Коммутативность
Б.а.о. * заданная на мн-ве А 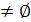 , коммутативна, если
, коммутативна, если  a,b
a,b 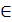 A a*b=b*a
A a*b=b*a
2.Ассоциативность
б.а.о. * на А 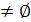 , ассоциативна, если
, ассоциативна, если  a,b,c
a,b,c 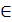 A (a*b)*c=a*(b*c)
A (a*b)*c=a*(b*c)
3.Дистрибутивность
Б.а.о * на А 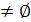 дистрибутивна, если
дистрибутивна, если  a,b,c
a,b,c 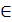 A
A
а*(b 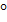 c)=(a*b)
c)=(a*b)  (a*c) – слева относительно *
(a*c) – слева относительно *
(a 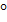 b)*c=(a*c)
b)*c=(a*c)  (b*c) – cправа относительно *
(b*c) – cправа относительно *
4. б.а.о. * на А 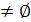 сократима, если
сократима, если  a,b,c
a,b,c 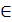 A
A
а*с = b*c => a=b (справа)
с*a=c*b => a=b (слева)
«+,-» - сократимые б.а.о.
“ 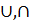 ” – не сократимые б.а.о
” – не сократимые б.а.о
5. Нейтральный элемент
Элемент е 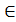 A (А
A (А 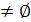 ) наз. Левым (правым) нейтральным относительно б.а.о * на А, если
) наз. Левым (правым) нейтральным относительно б.а.о * на А, если  a
a 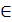 A: е*а=а (а*е=а)
A: е*а=а (а*е=а)
Элемент е 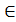 A (А
A (А 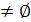 ) наз. нейтральным относительно б.а.о * на А, если
) наз. нейтральным относительно б.а.о * на А, если  a
a 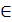 A: е*а=а*е=а
A: е*а=а*е=а
Т1 Если нейтральный элемент на множества А существует то он единственный
■e,e’ – нейтральные элементы на множестве А относительно *
e=e*e’=e’=>e=e’■
6. Симметричный элемент
Элемент a’ 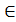 A (А
A (А 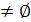 ) наз. Левым (правым) симметричным для a
) наз. Левым (правым) симметричным для a 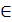 A если a’*а=e (а*a’=e)
A если a’*а=e (а*a’=e)
Элемент a’ 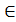 A (А
A (А 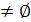 ) наз. симметричным для a
) наз. симметричным для a 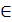 A если a’*а=а*a’=e
A если a’*а=а*a’=e
a' обозначается a-1 при этом а называется симметризуемым
Т2 Если бао * ассоциативна на непустом А и элемент а симметричен то существует единственный симметричный элемент для а
■a’, a’’ – симметричные для а элементы
a’*a=a*a’=e, a’’*a=a*a’’=e
a’=a’*e=a’*(a*a’’)=(a’*a)*a’’=e*a’’=a’’=>a’=a’’■
Опр. Подмножество В множества А называется замкнутым относительно операции * если для любых a,b принадлежащих В а*b принадлежит В
Зам. Если для обозначение операции используется знак сложения «+», то применяется адитивная форма записи
a+b-сумма,0-нейтральный,-а – симметричный (противоположный)
Если используется операция «∙» - мультипликативная форма записи
a∙b-произведение,1-нейтральный,a-1 – симметричный (обратный)
13) Алгебры с одной б.а.о. Полугруппа. Моноид. Группа.
Алгеброй называется упорядоченная пара (А, Ω), состоящая из А≠Ø (основное множество алгебры) и Ω (совокупность операций на множестве А – главные операции алгебры).
А =<А, Ω >
Тип алгебры А =<А,f1,…,fk> - это последовательность, состоящая из рангов n-арных операций, т.е. (rang (f1),…,rang (fk))
Алгебра g=<G,*> типа (2) называется полугруппой, если *-ассоциативна => G - полугруппа.
Алгеброй g=<G,*,1> типа (2,0) называется моноидом, если:
1) * - б.а.о. – ассоциативна на G
2)  нейтральный элемент в g относительно б.о. *, т.е. моноид – это полугруппа с нейтральным элементом. Моноид – полугруппа с 1.
нейтральный элемент в g относительно б.о. *, т.е. моноид – это полугруппа с нейтральным элементом. Моноид – полугруппа с 1.
Алгебра g=<G,*,’> типа (2,1) называется группой, если:
1) * - ассоциативна, т.е. (a*(b*c))=(a*b)*c
2) 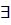 e ϵ g:a*e=e*a=a, ∀ a ϵ g
e ϵ g:a*e=e*a=a, ∀ a ϵ g
3) ∀ x ϵ g 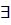 x’ ϵ g:x*x’=e
x’ ϵ g:x*x’=e
Группа – это моноид, в котором каждый элемент симметризуем.
Группа с коммутативной операцией называется коммутативной или абилевой
Если множество А конечно то можно составить таблицу кеш
Таблица кеш – таблица, которая описывает структура алгебраических систем с одной бинарной операцией
14) Алгебры с двумя а.о. Кольца. Поля.
Алгебра 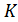 =(K,+,*) – типа (2,2) – наз. Кольцом (не ассоциативным), если для операций наз. Сложением и умножением выполн. След. Св-ва.
=(K,+,*) – типа (2,2) – наз. Кольцом (не ассоциативным), если для операций наз. Сложением и умножением выполн. След. Св-ва.
1.) Коммутативность 
2.) Ассоциативность 
3.) 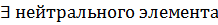

4.) 
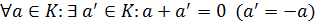
5.) Дистрибутивность 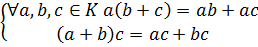
Если умножение в кольце коммутативно, то кольцо наз. Коммутативным кольцом
Если умножение в кольце ассоциативно, то оно наз. Ассоциативным кольцом
Если. < 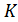 , ∙ > - полугруппа, тогда эта структура наз. Мультипликативной полугруппой кольца
, ∙ > - полугруппа, тогда эта структура наз. Мультипликативной полугруппой кольца
Если относительно умножения в кольце есть нейтральный эл-т 1, то кольцо наз. Кольцом с единицей
Не нулевой эл-т кольца А наз. Левым (правым) делителем 0, если 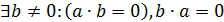 т.е
т.е 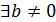 (b
(b 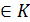 ):
): 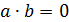 для
для 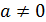 => a – левый делитель нуля
=> a – левый делитель нуля
Если умножение в кольце коммутативно, то левые и правые делители совпадают.
Алгебра <F,+, ∙> наз. Полем, если для б.о. +,* выполняются след. Св-ва
1) a+b=b+a
2) a+(b+c)=(a+b)+c
3) ∃0∈F: a+0=a
4) ∀ a∈F ∃! a’∈F: a+a’=0
5) (a*b)*c=a*(b*c)
6) a*b=b*a
7) ∃ 1∈F: a*1=a
8) ∀ a≠0 ∃ a’∈F: a*a’=1
9) 1≠0
10) a(b+c)=ab+ac
<F,+> - абелева адитивная группа поля
<F\{ 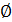 },∙> - мультипликативная группа поля
},∙> - мультипликативная группа поля
Поле – это ассоциативное, коммутативное кольцо с 1, в которой 0 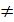 1 и каждый не нулевой эл-т обратим.
1 и каждый не нулевой эл-т обратим.
Элемент а называется обратимым (делитель 1) в кольце К, если для него существует обратный элемент в этом кольце
Существует a’ из К a∙a’=a’∙a=a
15) Гомоморфизм алгебр.
Пусть А =<A, Ω >, B =<B, Ω ‘> - однотипные алгебры, т.е. главных операций Ω на А столько, сколько главных операций Ω’ на В.
Пусть fa – главная операция на А, fb – главная операция на В.
Отображение h: A →B сохраняет главную операцию fa, если ∀ а1…аn ϵ A h((fa)(a1…an))=fb(h(a1)…h(an)), где n – ранг операции fa.
Гомоморфизмом алгебры А→В называется отображение h:A→B, которое сохраняет все главные операции A.
Гомоморфизм h:A→B называется мономорфизмом, если h – инъективное отображение A→B.
Гомоморфизм h:A→B называется эпиморфизмом, если h – сюръективное отображение A→B.
Гомоморфизм h:A→B называется изоморфизмом, если h – биективное отображение A→B.
Гомоморфизм алгебры A→B называется эндоморфизмом.
Изоморфизм алгебры А на себя называется автоморфизмом.
16) Булевы алгебры и их основные свойства.

 Булевой алгеброй называется А ≠ Ø с двумя б.о. +,*, унарной операцией () – аналог отрицания и двумя выделенными элементами е1 и е2: для всех элементов a,b,c ϵ A верны следующие аксиомы:
Булевой алгеброй называется А ≠ Ø с двумя б.о. +,*, унарной операцией () – аналог отрицания и двумя выделенными элементами е1 и е2: для всех элементов a,b,c ϵ A верны следующие аксиомы:
А1) +,* - коммутативны
a+b=b+a
a*b=b*a
A2)+,* - ассоциативны
a+(b+c)=(a+b)+c и a*(b*c)=(a*b)*c
A3)+,*,  различные нейтральные элементы е1 и е2 ϵ А: ∀ a ϵ A=>a+e1=e1+a=a; a*e1=e1*a=a
различные нейтральные элементы е1 и е2 ϵ А: ∀ a ϵ A=>a+e1=e1+a=a; a*e1=e1*a=a
A4)+,* - дистрибутивны относительно друг друга
a+(b*c)=(a+b)*(a+c)
a*(b+c)=(a*c)+(a*c)
A5) ∀ a ϵ A a+a=e2
a*a=e1 – свойство дополнительности
В булевой алгебре справедлив принцип двойственности т.е. в булевой алгебре существует двойственные утвержденияя: они либо одновременно верны либо не верны
Если в формуле верной в некоторой булевой алгебре поменять + на *, а * на +, и е1 на е2, а е2 на е1 то получится формула также истинная в этой булевой алгебре
Свойства:
1) е1 и е2 – единственны
2) ∀ a ϵ A 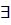 ! а ϵ А:a+a = e2, a*a=e1 – свойство отрицания
! а ϵ А:a+a = e2, a*a=e1 – свойство отрицания
3) Законы иденпотентности: ∀ a ϵ A а+а=а
а*а=а
4) Законы идентичности: ∀ a ϵ A а+е2=е2+а=е2
а*е1=е1*а=е1
5) Закон поглощения: ∀ a,b ϵ A а+(a*b)=a
a*(a+b)=a
6) Закон инвалюции ∀ a ϵ A а=а
7) Закон Де Моргана ∀ a,b,c ϵ A a+b=a*b
a*b=a+b
8) Закон дополнения: е1=е2; е2=е1
9) Закон склеивания: (a+b)*(a+b)=b
(a*b)+(a*b)=b
17) Алгебраические системы. Решетки. Примеры.
На непустом множестве А кроме алгебраич операц, можно рассматривать и отношения.
Def: алгебраич система – упорядоч тройка < 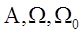 >, где
>, где  пусто,
пусто, 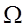 - мн-во алгебраич операций,
- мн-во алгебраич операций,  - мн-во отношений, заданных на А.
- мн-во отношений, заданных на А.
Частные случаи:
1.  = пусто, то <
= пусто, то <  >- алгебра
>- алгебра
2. 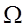 =пусто, то <
=пусто, то <  > - модель
> - модель
Решетки
Def: решеткой наз частично упорядочен мн-во <A, 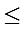 >, в кот каждое двухэлементное подмножество имеет как точную верхнюю (sup) и inf грани.
>, в кот каждое двухэлементное подмножество имеет как точную верхнюю (sup) и inf грани.
Для задания элементов х,у 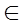 А inf{x,y} наз пересечением х и у и обознач через
А inf{x,y} наз пересечением х и у и обознач через 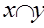 , а sup{x,y} наз объединением
, а sup{x,y} наз объединением 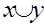 .
.
Замечания.
Операции 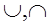 здесь понимаются, как абстрактные операции алгебраич системы и отличные от теоретико-множественных операций
здесь понимаются, как абстрактные операции алгебраич системы и отличные от теоретико-множественных операций 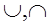 , определяемых в алгебре множеств (в частных случаях они могут совпадать)
, определяемых в алгебре множеств (в частных случаях они могут совпадать)
В системе А введены операции 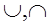 , то тогда отношение частичного порядка
, то тогда отношение частичного порядка 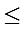 можно по этим операциям восстановить след образом:
можно по этим операциям восстановить след образом:
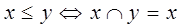
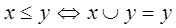
Def: наименьший (наибольший) элем решетки, если он существует, наз нулем(единицей) и обознач 0(1).
Утверждение. В конечных решетках всегда имеется 0 и 1.
Пример.
1. Любое конечное лин упоряд мн-во явл решеткой.
2. |A|>1, то ЧУМ <A, idA>, где idA={(x,x)/x 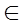 A} – тождеств отношение не явл решеткой, поскольку
A} – тождеств отношение не явл решеткой, поскольку 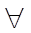 x и у - различных не определена операция inf{x,y} и sup{x,y}.
x и у - различных не определена операция inf{x,y} и sup{x,y}.
Def: решетка А=< A, 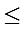 > наз дистрибутивной, если
> наз дистрибутивной, если 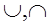 - дистрибутивны, т.е
- дистрибутивны, т.е 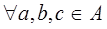
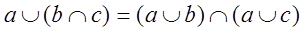 и
и 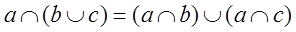
Def: дистрибут решетка А=< A, 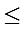 > наз булевой алгеброй, если А имеет 0,1 и 0
> наз булевой алгеброй, если А имеет 0,1 и 0 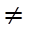 1 и
1 и 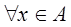
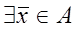 :
: 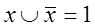 и
и  .
.