8.1. Метод Бубнова–Галеркина. Метод предложил в 1913г. И.Г. Бубнов в своем отзыве на одну из работ С.П. Тимошенко, и, независимо от него, Б.Г. Галеркин в 1915г.; метод базируется на свойстве ортогональных функций и имеет второе название – метод ортогонализации. В курсе математического анализа дается следующее определение ортогональных функций: если имеется семейство непрерывных функций
 (𝑥),
(𝑥),  (𝑥),
(𝑥),  (𝑥), …,
(𝑥), …,  (𝑥),
(𝑥),  (𝑥), …,
(𝑥), …, 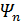 (𝑥), (а)
(𝑥), (а)
и интеграл от произведения любых двух различных функций этого семейства в промежутке  равен нулю:
равен нулю:
 (б)
(б)
то функции (a) образуют в этом промежутке ортогональную систему. На основании леммы из курса математического анализа следует, что если одна из функций тождественно равна нулю, например  (𝑥) ≡ 0, то она ортогональна ко всем без исключения функциям, так как в этом случае условие (б) выполняется. В качестве примера такой функции можно привести функцию
(𝑥) ≡ 0, то она ортогональна ко всем без исключения функциям, так как в этом случае условие (б) выполняется. В качестве примера такой функции можно привести функцию
 (𝑥) = EI
(𝑥) = EI  ‒ 𝑞, (в)
‒ 𝑞, (в)
представляющую собой дифференциальное уравнение изогнутой оси балки. Эта функция есть тождественный нуль при любых значениях 𝑥 и, следова-
тельно,
 (г)
(г)
Здесь интеграл берется вдоль всей длины балки 𝐿, и значит функция (в) ортогональна в промежутке  к любой функции.
к любой функции.
Если функцию 𝑤=𝑤(𝑥) заменить ее приближенным значением в форме ряда:
 (д)
(д)
то функция (в) уже не будет тождественно равна нулю, а значит, и не будет ортогональна в промежутке  к любой функции.
к любой функции.
Можно потребовать, чтобы полученная функция была ортогональна хотя бы к ограниченному классу функций, например функций  , составляющих ряд (д), т. е. чтобы
, составляющих ряд (д), т. е. чтобы
 (е)
(е)
(𝑖= 1, 2, 3, …, 𝑛)
В результате получаем 𝑛 линейных уравнений для определения 𝑛 постоянных коэффициентов  , входящих в ряд (д).
, входящих в ряд (д).
На использовании системы уравнений (е) для определения значений параметров  основан метод Бубнова ‒ Галеркина для одномерной задачи.
основан метод Бубнова ‒ Галеркина для одномерной задачи.
Все рассуждения, приведенные для функции одного аргумента, можно применить и к функциям двух и более аргументов. Рассматриваемый метод является частным случаем обобщенного метода Бубнова‒Галеркина, если выбранные выражения для перемещений, наряду с кинематическими граничными условиями, удовлетворяют также и силовым условиям.
Для решения геометрически линейных задач, например, двумерной задачи об изгибе пластинок, уравнения Бубнова ‒ Галеркина (е) можно представить в следующем виде:
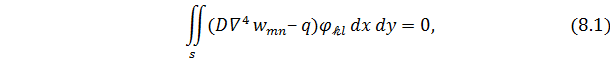
(𝓀 = 1, 2, 3, …, 𝑚; 𝑙 = 1, 2, 3, …, 𝑛)
где вместо промежутка  на оси рассматривается плоская область 𝑠, ограниченная контуром пластинки, а функция
на оси рассматривается плоская область 𝑠, ограниченная контуром пластинки, а функция  представлена в виде следующего двойного ряда по области 𝑠:
представлена в виде следующего двойного ряда по области 𝑠:
 (ж)
(ж)
Таким образом, в уравнениях (8.1) приближенная функция, представляющая собой левую часть дифференциального уравнения изогнутой срединной поверхности пластинки С. Жермен - Лагранжа, ортогонализируется на области 𝑠 ко всем функциям 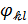 ряда (ж), входящим в эту приближенную функцию.
ряда (ж), входящим в эту приближенную функцию.
Методу Бубнова‒Галеркина можно дать следующее толкование. Функция

представляет собой проекцию на ось 𝑧 всех внешних и внутренних сил, действующих на бесконечно малый элемент пластинки. Функция прогибов  есть перемещение в направлении этой же оси. Значит, функции
есть перемещение в направлении этой же оси. Значит, функции 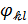 тоже являются перемещениями в направлении оси 𝑧 и их можно считать возможными перемещениями. Следовательно, уравнения Бубнова‒Галеркина (8.1) приближенно выражают равенство нулю работы всех внешних и внутренних сил в пластинке на возможных перемещениях
тоже являются перемещениями в направлении оси 𝑧 и их можно считать возможными перемещениями. Следовательно, уравнения Бубнова‒Галеркина (8.1) приближенно выражают равенство нулю работы всех внешних и внутренних сил в пластинке на возможных перемещениях 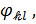 т.е. по сути своей этот метод является вариационным.
т.е. по сути своей этот метод является вариационным.
Метод Бубнова‒Галеркина, как и метод Ритца‒Тимошенко, исходит из принципа возможных перемещений, а поэтому оба метода равноправны. В обоих методах аппроксимирующую функцию необходимо выбирать так, чтобы она удовлетворяла геометрическим граничным условиям, а статическим‒необязательно.