МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к расчетно-графической работе
«Расчет балки-стенки»
по курсу «теория упругости и пластичности»
для студентов дневной и заочной форм обучения
по специальности промышленное и гражданское строительство
Новополоцк 2012
ВВЕДЕНИЕ
Методические указания предназначены для студентов специальности «Промышленное и гражданское строительство» дневной и заочной форм обучения. Расчет балки-стенки методом конечных разностей представлен теоретической частью, приводятся основные уравнения плоской задачи теории упругости, рассматривается методика составления бигармонического уравнения с выражением производных через конечные разности функции напряжений. Приводится числовой пример расчета балки-стенки и вопросы для подготовки к защите расчетно-проектировочной работы.
ОСНОВНЫЕ ФОРМУЛЫ, ОПРЕДЕЛЕНИЯ
Определение поля напряжений в балке-стенке осуществляется введением функции напряжений j(х, у). Бигармоническое уравнение плоской задачи записывается через функцию напряжения в следующем виде:
(1.1)
Внутри контура пластинки и на контуре функция напряжений должна удовлетворять уравнению (1.1), причем на контуре функция напряжений определяется с помощью рамной аналогии
(1.2)
Введением рамной аналогии определяется и первая производная функции напряжений в контурных точках в направлении нормали к
контуру.
(1.3)
В выражениях (1.2) и (1.3) M (S) – величина изгибающего момента в точке контура, a N (S) – продольная сила в точке К, если контур пластинки рассматривать как раму, подвергаемую изгибу внешней нагрузкой. Так как выражения (1.2), (1.3) справедливы для любой рамы, очерченной по контуру пластинки, рассматривается статически определимая рама или шарнирно-стержневой многоугольник. Определение M (S) и N (S) в стержнях указанных систем осуществляется наиболее просто.
Проинтегрировав уравнение (1.1) и определив функцию j(х, у), находим функции, определяющие поле нормальных и касательных напряжений в пластинке
(1.4)
Правило знаков для напряжений, моментов и продольных сил
Нормальные напряжения при растяжении положительны, при сжатии отрицательны.
Касательные напряжения положительны при совпадении с направлением координатной оси, отрицательны при противоположном направлении, если внешняя нормаль совпадает с положительным направлением другой оси.
Изгибающие моменты положительны при расположении эпюры M(S), построенной на растянутом волокне, внутри контура рамы и отрицательны при расположении на наружной стороне контура.
Продольная сила положительна при растяжении, отрицательна при сжатии стержней рамы.
МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Метод конечных разностей является одним из методов приближенного интегрирования бигармонического уравнения (1.1). При реализации метода функция напряжений определяется дискретно, для чего область определения функции заменяется сеткой, в узлах которой и определяются значения функции напряжений. Бигармонические уравнения (1.1), где частные производные представлены в конечно-разностной форме, составляются для каждого узла сетки. В результате чего получается система алгебраических уравнений, неизвестными которых являются значения функции напряжений в узлах сетки внутри контура пластинки.
Рассмотрим, как определяются производные функции в некоторой точке через ее значения в смежных точках на примере функции одной переменной. На рис. 1 изображен график функции j(х), значения которой вычислены в точках а, d, с, d, i.
Рис.1
Определяем первую производную в точке i. При малости интервала l первая производная в точке i определяется следующим приближенным равенством
Вторая и последующие производные определяются аналогично
Если рассматривается функция двух переменных j(х, у), то частные производные в узле сетки i (рис. 2) определяются аналогично.
Рис. 2
(2.1)
(2.2)
(2.3)
Заметим, что с помощью выражений (2.2) определяют нормальные и касательные напряжения в точке i через значения функции напряжений в смежных точках.
Подставляем выражения четвертых производных (2.3) в уравнение (1.1), получая алгебраическое уравнение, неизвестными которого являются значения функции напряжений в точке i и окрестных точках. В случае квадратной сетки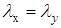 
это уравнение запишется в виде:
(2.4)
Уравнение (2.4) составляется для каждого внутреннего узла сетки. При этом в качестве смежных точек «захватываются» точки вне контура пластинки, что увеличивает число неизвестных в полученной системе. Однако значение функции напряжений в законтурных точках можно определить с помощью рамной аналогии через значения функции в смежных внутриконтурных точках и продольной силы N в точке контура. Запишем значения j в законтурных точках по границам пластинки (рис. 3).
Верхний край 
Нижний край 
(2.5)
Левый край 
Правый край 
Рис. 3
Заменив в уравнениях (2.4) значения j в законтурных точках по выражениям (2.5), получаем систему разрешающих уравнений для внутриконтурных точек. Определив значения j во внутриконтурных точках, находим нормальные и касательные напряжения по выражениям (2.2) и строим их эпюры.