ПЛАН
1. Развитие понимания сохранения количества и величины у детей дошкольного возраста
2. Методика использования творческих задач, вопросов и ситуаций в обучении дошкольников
3. Алгоритмы и их освоение дошкольниками.
4. Моделирование как средство логико-математического развития детей дошкольного возраста
5. Методика развития моделирования у детей дошкольного возраста.
6. Реализация идеи интеграции в логико-математическом развитии дошкольников
7. Логико-математическое и экономическое развитие дошкольников
8. Логико-математическое развитие и освоение краеведческих представлений дошкольниками
9. Логико-математическое и речевое развитие дошкольников
10. Логико-математическое и физическое развитие дошкольников
11. Логико-математическое и художественно-эстетическое развитие дошкольников
12. Логико-математическое и социально-личностное развитие дошкольников
1. Развитие понимания сохранения количества и величины у детей дошкольного возраста
Осуществляя целенаправленное различение, называние, упорядочивание и сравнение свойств, ребенок учится устанавливать взаимосвязи относительно признаков форм, количеств и выражать их с помощью языковых средств. При определении взаимосвязей дети дошкольного возраста опираются в основном на собственный опыт, который, однако, организуется взрослыми.
Когда речь идет об обучении дошкольников, имеется в виду не прямое обучение логическим операциям и отношениям, а подготовка детей посредством практических действий к усвоению смысла слов, обозначающих эти операции и отношения.
По своему содержанию эта подготовка не должна исчерпываться только развитием математических представлений. С точки зрения современной концепции обучения самых маленьких детей не менее важным, чем арифметические операции, является развитие элементов логического мышления. Детей до школы необходимо учить не только вычислять и измерять, но и рассуждать.
В развитии элементов логико-математического мышления ребенка есть важная граница, которую большинство детей переходят между 5 и 8 годами, — понятие о сохранении. Понимание сохранения количества создает предпосылку для формирования понятия о количественном числительном.
Понятие о сохранении требует осознания детьми того факта, что определенные свойства (например, количество, масса) не меняются при изменении других свойств (плотности расположения элементов, формы).
Всемирно известный швейцарский психолог Жан Пиаже обоснованно считал, что понимание сохранения объекта в процессе изменения его формы составляет важное условие всякой рациональной деятельности, необходимое условие математического мышления.
Процедура постановки задач Пиаже на сохранение следующая. Ребенку показывают два совершенно одинаковых предмета или два совершенно одинаковых набора предметов (два одинаковых шарика или две одинаковых колбаски из пластилина; два одинаковых стакана, заполненные одинаковым количеством воды; два ряда, содержащие одинаковое количество каких-либо предметов; две одинаковые палочки, расположенные параллельно и так, что их концы совпадают; два одинаковых предмета одинакового веса). Ребенка просят оценить количество пластилина в объектах, воды в стаканах, предметов в рядах, массы объектов и длины палочек.
После того как правильная оценка получена, экспериментатор на глазах у ребенка трансформирует один из стимулов: раскатывает, сжимает или расплющивает один из кусочков пластилина, переливает воду из одного из стаканов в стакан другой формы и размера, раздвигает или приближает друг к другу объекты в одном из рядов, сдвигает палочки так, что совпадение их концов нарушается. То есть сначала показываемые ребенку объекты одинаковы по всем своим свойствам, а после трансформации — только по одному из свойств, сохранение которого проверяется (количество пластилина в кусочках; длина палочек, количество предметов в рядах). Что же касается других свойств, то теперь их значения в двух объектах становятся разными. Эти различия могут быть описаны как различия по форме и пространственным отношениям, а более детально — как различия по элементам формы — по длине, толщине, высоте, ширине, конфигурации, плотности объектов в рядах, взаимном расположении предметов и рядов. После этого ребенка опять просят оценить равенство или неравенство объектов по тем же свойствам, равенство которых признавалось до трансформации. Если теперь ребенок отрицает равенство по тем свойствам, которые не изменялись при трансформации, то такой ребенок «не сохраняет» количество, длину, вес.
Например, вы можете показать ребенку два равных ряда бусинок и спросить, одинаковы ли они. Если ребенок понимает, о чем вы спрашиваете, он ответит «да». Если затем изменить один ряд, и спросить, остались ли ряды одинаковыми или в одном ряду стало больше бусинок, ребенок может ответить, что в длинном ряду бусинок больше. Это означает, что он не обратил внимания на неизменность количества бусинок и использовал длину ряда в качестве ключа.
Ребенок, начинающий овладевать понятием сохранения количества, скажет, что оба ряда имеют одинаковое количество бусинок, потому что в рядах по 5 бусинок — или просто потому что ничего не добавили и не убрали. Ребенок, владеющий понятием сохранения, скажет, что в обоих рядах находится одинаковое количество бусинок, независимо от того, что сделает воспитатель — расположит их определенным рисунком или разложит на кучки.
Аналогичным образом проводится опыт с водой или другой жидкостью. Ребенку показывают две одинаковые банки с жидкостью, а затем переливают жидкость одной из них в высокую узкую или в широкую банку ил и в две меньшие банки. Если ребенок усвоил понятие сохранения вещества, он скажет, что после переливания в другой банке содержится такое же количество жидкости.
Можно сделать два равных шарика из пластилина, а затем раскатать один из них в жгутик или превратить его в блинчик или же в два шарика меньших размеров. Ребенок, освоивший понятие сохранения, способен понять, что в нераскатанном и в раскатанном шарике одно и то же количество пластилина при условии, что ничего не добавили и ничего не убавили.
Таким образом, сущность сохранения проявляется в ситуациях преобразования объектов. Сначала предъявляемые ребенку объекты одинаковы по всем своим свойствам, а после трансформации — только по одному из свойств, сохранение которого проверяется.
Сохранение количества дискретных твердых предметов (бусин, пуговиц, чашек) в наборе можно установить счетом. При этом можно менять взаимное расположение элементов, составляющих набор, но не сами эти элементы. Деформируемые, непрерывные материалы (жидкости, глина, бечевка, резиновая лента) не поддаются счету. Меру им можно придать только с помощью измерительных устройств: линеек, весов, градуированных емкостей и др. Вот почему раньше приобретается понятие о сохранении количества вещества, затем — массы и в последнюю очередь — объема.
Ж. Пиаже определил три последовательные стадии в развитии у детей способности к сохранению.
Первая стадия (стадия несохранения) — это глобальное качественное сравнение. На этой стадии параметр (масса, количество, размер) еще не отделяется ребенком от других свойств предмета. Поэтому дети, например, не способны подобрать столько же элементов, сколько их содержится в предъявленном множестве. Они приблизительно воспроизводят общую форму предъявленной совокупности, тогда как количество объектов во второй совокупности может быть большим или меньшим, чем в первой. Например, линейные ряды копируются по их длине, независимо от плотности элементов в ряду.
На этой стадии дети утверждают, что количество вещества, его вес и объем изменяются при изменении формы глиняного шарика или сосуда, в который переливается вода или пересыпаются бусины. Если шарик превращается в более длинную колбаску, они говорят, что в нем стало больше глины, что он стал тяжелее и что вода в сосуде, в которую его опустят, поднимется выше. Если воду перелили в более высокий и тонкий сосуд так, что ее уровень стал выше, чем в стандартном, дети говорят, что в новом сосуде воды стало больше и т. п.
Таким образом, на первой стадии ребенок может правильно оценить объект только в конкретной ситуации на основе непосредственного восприятия предметов.
Вторая стадия развития (неустойчивое сохранение) характеризуется неустойчивостью ответов и тем, что дети утверждают сохранение количества, величины при незначительных трансформациях объектов и отрицают сохранение при больших трансформациях. Например, когда произведенная трансформация формы глиняного шарика невелика или когда второй сосуд не очень отличается от стандартного, дети говорят, что вещества (массы, объема) осталось столько же. Но когда трансформация формы более значительна, вновь даются ответы о несохранении. На этой стадии старший дошкольник способен отвлекаться от наиболее ярких свойств и может оценивать отношения между предметами на основе менее заметных, скрытых свойств, т. е. опосредованно. Например, он уже знает, что раздвинутые пальцы ладони хотя и занимают больше места в пространстве, чем сжатые кулаки, но между ними при этом увеличивается лишь расстояние.
Наконец, на третьей стадии (стадии сохранения) дети уверенно проявляют понимание сохранения при любых трансформациях. Дети, находящиеся на этой стадии, ясно понимают, что количество элементов в двух совокупностях остается одинаковым, как бы экспериментатор ни изменял форму и площадь созданных ими конфигураций.
Усвоение понятия сохранения тесно связано с общей способностью ребенка мыслить и рассуждать, дифференцировать разные свойства и избирательно оперировать каким-либо из них, абстрагируясь от других. Дифференциация разных свойств, умение выразить их в речи — длительный процесс, растягивающийся на годы.
Вначале, когда такой дифференциации нет, восприятие объектов интегрально, и столь же интегрально представлены свойства в высказываниях детей. Отсюда — все феномены несохранения, характерные для первой стадии. Количественные свойства объектов (количество вещества, масса, объем) еще не выделены в восприятии и в речи из их общей формы, слиты с ней. При этом в силу глобальности и малой расчлененности самой формы, как в восприятии, так и в высказываниях, при оценке и сравнении количеств принимается во внимание только наиболее резко выступающие, «бросающиеся в глаза» качества формы: длина колбаски или площадь поверхности, высота столбика воды в сосуде. По этим свойствам выносятся первые грубые суждения детей: больше, меньше, равно. Менее выступающие и меньше бросающиеся в глаза особенности формы, такие как толщина колбаски и глиняной лепешки (когда она невелика и явно меньше высоты), не оказывают влияния на суждения о величине.
В дальнейшем, когда восприятие и речь детей становятся более дифференцированными, они могут сравнить величины по одной, но по разным особенностям формы. Отсюда возможность неустойчивых рассуждений. Вместе с тем, когда определенное количество уже начинает выделяться из «упаковки», не очень большие изменения формы могут не сказываться на оценках величины, в отличие от значительных ее трансформаций. Отсюда — еще один источник неустойчивости рассуждения детей на второй стадии. Только на третьей стадии в результате длительного процесса «освобождения» от внешних несущественных признаков количество становится инвариантным при любых изменениях формы, что обеспечивает его устойчивое сохранение.
Проведенное Л. Ф. Обуховой и П. Я. Гальпериным исследование показало, что развитие умения выделять в сравниваемых объектах разные свойства и каждое из них измерять с помощью какой-то избранной мерки представляет собой необходимое условие для формирования у детей полноценного знания о принципе сохранения.
Американский психолог Дж. Брунер установил, что если 5— 6-летних детей, не обнаруживших понимания принципа сохранения, тренировать в обратном преобразовании предмета, например из «колбаски» снова сделать шарик, и при этом ставить перед ребенком вопрос «Получились одинаковые шарики?», то после серии таких тренировок у большинства детей обнаруживается понимание принципа сохранения, т. е. они переходят с первой на третью стадию развития познавательной способности оценки величин и количеств.
Все эти факты свидетельствуют о том, что целенаправленное обучение способствует освоению понятия сохранения дошкольниками. Основной путь в таком обучении — развитие умения дифференцировать разные свойства, что достигается через развитие у детей действия сравнения, освоение ими операций сериации и классификации. Овладение счетом и измерением также способствует развитию понимания сохранения количества, величины.
Как отмечают многие исследователи, обучая сохранению, важно создавать ситуации, в которых ребенок оказывается в познавательном конфликте. Например, если ребенок склонен полагать, что удлинение шарика увеличивает количество пластилина, а убавление (отщипывание) кусочка уменьшает его количество, необходимо произвести сразу и одну, и другую операции. Это заставит ребенка колебаться между взаимно конфликтующими стратегиями, более внимательно оценивая ситуацию.
В процессе усвоения понятия сохранения детей и активно входят в практику образовательного процесса благодаря развитию метода обучения ТРИЗ — Теории Решения Изобретательских Задач. Творческие задачи (вопросы, ситуации) имеют много решений (которые будут правильными), но не имеют четкого алгоритма (последовательности) решения. Эти средства прежде всего направлены на развитие смекалки, сообразительности, воображения, творческого (дивергентного) мышления как важного компонента творческих способностей. Они способствуют переносу имеющихся представлений в иные условия деятельности, а это требует осознания, присвоения самого знания. В процессе решения творческих задач ребенок учится устанавливать разнообразные связи, выявлять причину по следствию, преодолевать стереотипы (которые уже начинают складываться), комбинировать, преобразовывать имеющиеся элементы (предметы, знания, вещества, свойства). Но самое главное — в процессе решения таких задач ребенок начинает испытывать удовольствие от умственной работы, от процесса мышления, от творчества, от осознания собственных возможностей.
2. Методика использования творческих задач, вопросов и ситуаций в обучении дошкольников
Ю. Г. Тамберг отмечает, что существуют определенные трудности в выборе задач для детей. Если задача простая — ребенку скучно, если сложная — он отказывается ее решать. Существует несколько уровней трудности задач. Первый — ребенок может решить задачу самостоятельно. Второй — самостоятельно решить не может, но с помощью наводящих вопросов решает сам. Третий — не может решить, но может понять ход решения и ответ. Четвертый — не может ни решить, ни понять ход решения, ни понять ответ. Следует давать задачи первых трех уровней сложности, причем третий уровень задач надо решать в режиме «Давай решим вместе». Это воспитывает в ребенке уверенность в своих силах, смелость в постановке целей, доставляет удовольствие от общения со взрослым.
Дошкольникам целесообразно предъявлять творческие задачи, ставить творческие вопросы после того, как необходимые для решения представления уже имеются у ребенка. Например, творческая задача «Нарисуй кошку, не рисуя ее» предполагает одним из вариантов решения рисование какой-либо части, по которой можно догадаться о целом (знание о зависимости части и целого). Задача «Нарисуй медведя в квадрате со стороной в 2 клетки, но так чтобы он был самым большим!» требует осознания относительности величины.
Творческая задача «Как нарисовать солнце, если наш карандаш умеет рисовать только квадраты?» может быть решена через осознание структуры геометрических фигур: чем больше углов, тем больше фигура похожа на круг. Это задача третьего уровня для шестилеток. Можно предложить решать ее практическим способом: множество квадратов накладывать друг на друга, моделируя солнце, или же выстраивать из них замкнутую в круг линию.
Творческий вопрос «Что надо сделать, чтобы сапоги не скользили в гололед?» заставляет детей задуматься о причине скольжения, а также о том, какие свойства (сапога, льда) и как нужно изменить, чтобы найти правильный ответ. Совместное обсуждение этого вопроса позволит найти несколько приемлемых решений и подарит детям радость содержательного общения.
Результатом включения в образовательный процесс творческих задач, ситуаций, вопросов будет развитие у детей (и взрослых) творческих способностей, уточнение и углубление представлений о разнообразных свойствах, связях, отношениях и зависимостях, развитие инициативности, самостоятельности, уверенности в своих возможностях, чувства юмора и удовольствия от умственного труда и общения.
Формы организации детской деятельности зависят от вида, назначения игр, мотивации, степени овладения познавательными действиями.
Преимущественно самостоятельно и инициативно, в виде самодеятельности дети осваивают настольно-печатные игры, игры-забавы, логические и математические головоломки, занимаются экспериментированием. Естественно, что в каждом конкретном случае возможно сочетание самодеятельности и совместного со взрослым конструирования системы игровых действий, обсуждения их результативности, проектирования хода игры и т.д. Взрослый мотивирует деятельность детей, создает положительное настроение, стремление находить способы решения, отгадывать и догадываться, включаться в коллективное решение игровых задач.
В деятельности, организуемой взрослым, дети осваивают способы разрешения проблемных ситуаций, решения творческих задач, поиска и построения ответа на вопрос. Для этого взрослый организует тематические мини-ситуации, занятия в виде сюжетных логико-математических игр, тренинги, развлечения и вечера досуга (в том числе совместные с родителями).
3. Алгоритмы и их освоение дошкольниками.
Воспитание детей с самого рождения, в частности воспитание дошкольников, включает усвоение ими разного рода правил и их строгое выполнение (правила утреннего туалета, одевания и раздевания, принятия пищи, перехода улицы). Режим дня дошкольника представляет собой систему предписаний о выполнении детьми и воспитателем действий в определенной последовательности. Обучая детей счету, измерению длин, сложению и вычитанию чисел, уборке комнаты, посадке растений и т. д., мы сообщаем им необходимые правила о том, что и в какой последовательности нужно делать для выполнения задания. Организовывая разнообразные дидактические и подвижные игры, мы знакомим дошкольников с их правилами.
О всех видах деятельности, осуществляемых по определенным предписаниям, говорят, что они выполняются по определенным алгоритмам. С малых лет человек усваивает и исполняет в каждодневной жизни большое число алгоритмов, часто даже не зная, что это такое.
Что такое алгоритм? Нередко встречаются виды однотипных задач, например: сложение двух многозначных чисел; переход улицы, регулируемый или нерегулируемый светофором; измерение длины отрезка и т. д. Естественно возникает вопрос: существует ли достаточно общий способ, который можно было бы использовать для решения любой задачи данного вида однотипных задач? Если такой общий способ существует, то его называют алгоритмом^ данного вида задач. Для каждого из приведенных выше видов задач имеется соответствующий алгоритм.
Слово алгоритм происходит от имени известного математика IX в. аль-Хорезми, что означает «из Хорезма», впервые сформулировавшего правила выполнения арифметических действий над многозначными числами. Через труды аль-Хорезми в Европу проникли способы действий с числами в десятичной системе счисления, которые стали называть алгоритмами согласно латинской транскрипции имени ученого. В течение столетий значение слова «алгоритм» постепенно обобщалось, и сегодня под алгоритмом понимают некоторый общий метод или способ, предписание, инструкцию, свод правил для решения за конечное число шагов любой задачи из определенного вида однотипных задач, для которого предназначен этот метод.
Для задачи сложения двух многозначных чисел известен способ сложения «в столбик», пригодный для сложения любых двух многозначных чисел, т. е. для решения любой частной задачи из этого вида однотипных задач.
Для задачи перехода улицы, например нерегулируемого светофором, можно сформулировать общий способ в виде следующего предписания, состоящего из 10 указаний, или команд:
1. Подойди к краю тротуара у знака перехода.
2. Стой.
3. Смотри налево.
4. Если идет транспорт слева, то перейди к указанию 2, иначе — к указанию 5.
5. Пройди до середины улицы.
6. Стой.
7. Смотри направо.
8. Если идет транспорт справа, то перейди к указанию 6, иначе — к указанию 9.
9. Пройди вторую половину улицы до противоположного тротуара.
10. Переход улицы закончен.
Интуитивно под алгоритмом понимают общепонятное и точное предписание о том, какие действия и в каком порядке необходимо выполнить для решения любой задачи из данного вида однотипных задач.
Это определение, разумеется, не является математическим определением в строгом смысле, так как в нем встречается много терминов, смысл которых хотя и интуитивно может быть ясен, но точно не определен («предписание», «общепонятное», «точное», «действие»). Однако оно представляет собой разъяснение того, что обычно вкладывается в интуитивное понятие алгоритма, а для наших целей этого вполне достаточно.
Какие же свойства характеризуют всякий алгоритм?
Анализ различных алгоритмов позволяет выделить следующие общие свойства, присущие алгоритмам:
а) массовость, т. е. алгоритм предназначен для решения не одной какой-нибудь задачи, а для решения любой задачи из данного вида однотипных задач;
б) определенность (или детерминированность), т. е. алгоритм представляет собой строго определенную последовательность шагов, или действий, он однозначно определяет первый шаг и каждый следующий шаг, не оставляя решающему задачу никакой свободы выбора следующего шага по своему усмотрению;
в) результативность: решая любую задачу из данного вида задач по соответствующему алгоритму, мы за конечное число шагов получаем результат. Разумеется, для различных частных задач одного вида число шагов может оказаться различным, но оно всегда конечно.
Алгоритм — одно из фундаментальных научных понятий, используемое и математикой, и информатикой — наукой, изучающей способы представления, хранения и преобразования информации с помощью различных автоматических устройств. Наличие алгоритма для осуществления некоторой деятельности является необходимым условием передачи этого вида деятельности различным автоматическим устройствам, роботам, компьютерам (от отпуска стакана газированной воды, продажи авиабилета с хранением и преобразованием информации о наличии свободных мест до управления сложными технологическими процессами, не говоря уже о выполнении огромных объемов вычислительной работы, связанной с решением сложных научно-технических задач).
Имеются различные формы записи или представления алгоритмов, предназначенные для различных исполнителей: словесные предписания, в том числе включающие различные формулы; наглядные блок-схемы, ориентированные на исполнителя-человека; программы, представляющие собой запись алгоритма на языке, понятном ЭВМ, т. е. языке программирования.
Здесь уместно уточнить, что означает выдвинутое требование «общепонятности» предписания, которым задается алгоритм. Это означает, что предписание должно быть сформулировано так, чтобы оно было одинаково понятно всем исполнителям той категории, на которую оно ориентировано. Это имеет чрезвычайно важное значение, в частности, при обучении маленьких детей. Например, приведенные выше предписания, задающие алгоритмы перехода улицы и измерения длины, не предназначены для обучения дошкольников. Для этой цели нужно сформулировать их на понятном детям языке, что и делает любой воспитатель, если, разумеется, он имеет соответствующую подготовку и понимает свои задачи.
Однако приведенные выше предписания составлены так, что они выявляют шаговую (дискретную) оперативно-логическую структуру алгоритмов. Поясним, что это означает.
1. Каждый алгоритм может быть представлен в виде последовательности шагов. Разумеется, понятие шаг является относительным. Один и тот же алгоритм можно по-разному представить в виде последовательности шагов, и не всегда отдельные шаги соответствуют элементарным действиям. Само понятие элементарное действие относительно: одно и то же действие может быть для одного ребенка, и не только ребенка, элементарным, для другого — неэлементарным (в результате чего и возникает необходимость в расчленении этого действия на другие, элементарные, действия).
Дискретность структуры алгоритма состоит в том, что для каждого шага можно указать однозначно непосредственно следующий за ним шаг.
2. В приведенных выше предписаниях можно различить два основных вида команд, а следовательно, два основных вида шагов, представленных этими предписаниями алгоритмов: простые команды, предписывающие выполнение некоторых действий («смотри влево», «пройди до середины улицы», «выбери мерку», «наложи мерку» и т. д.), и составные, определяющие разветвление процесса решения задачи в зависимости от выполнения или невыполнения некоторого условия («если идет транспорт слева, то перейди к указанию 2, иначе — к указанию 5»), называемые условными.
Условная команда имеет вид «если Р, то А, иначе В». Она предписывает следующий порядок действий: если условие Р выполняется (истинно), то выполняется А (в нашем примере — возврат к указанию 2). Если же условие Р не выполняется (ложно), что обозначается словом «иначе», то А пропускается и выполняется В (в нашем примере осуществляется переход к следующему указанию 5).
Условные команды можно записать сокращенно: «если Р, то А», при этом подразумевается, что если условие Р не выполняется, то осуществляется переход к следующей по порядку команде В приведенных выше примерах условные команды, если условие Р выполняется, определяют повторение некоторых действий («стой», «смотри влево», «смотри вправо», «наложи мерку» и т. д.) определенное число раз (пока условие Р выполняется). Такие процессы и соответствующие им алгоритмы, в которых некоторые действия повторяются, называются циклическими.
Если же алгоритм состоит из одних простых команд, то он называется линейным.
Таким образом, различают линейные, разветвленные и циклические алгоритмы.
Алгоритм можно наглядно представить в виде блок-схемы, состоящей из блоков и стрелок. Каждый шаг представляется с помощью блока. Блок, предусматривающий выполнение некоторого действия, изображается в виде прямоугольника, внутри которого записано соответствующее действие. Блок, представляющий логическое условие, изображается в виде ромба, внутри которого записано проверяемое условие. Если за шагом А непосредственно следует шаг В, то от блока А к блоку В проводится стрелка. От каждого прямоугольника исходит только одна стрелка, от каждого ромба — одна или две стрелки (одна с пометкой «да», идущая к блоку, следующему за логическим условием, если оно истинно, другая — с пометкой «нет», идущая к блоку, следующему за логическим условием, если оно ложно). Начало и конец изображаются овальными фигурами.
Алгоритмы, представленные выше с помощью словесных предписаний, могут быть представлены и с помощью блок-схемы, иными словами, эти предписания переводятся в блок-схемы.
На иллюстрация изображена блок-схема алгоритма перехода улицы, нерегулируемого светофором.
Для изображения алгоритмов некоторых детских игр (правил игры) могут быть использованы специальные условные обозначения, которые легко разъясняются детям.
Приведем в качестве примера игру «Преобразование слов», моделирующую понятие 
алгоритм преобразования слов в данном алфавите. В этой игре, а по существу серии игр, буквы и слова необычные. Используется двухбуквенный алфавит, состоящий из двух различных геометрических фигур, например квадратика и кружочка, или из цифр 0 и 1. Словами мы называем конечные цепочки из квадратиков и кружочков (во втором варианте конечные последовательности из нулей и единиц). Любое сколь угодно длинное слово в нашем алфавите преобразовывается по приведенным на иллюстрации правилам следующим образом: если в заданном слове имеется квадратик, расположенный левее кружочка, то, согласно правилу 1, их нужно поменять местами; если во вновь полученном слове опять имеется квадратик, расположенный левее кружочка, нужно опять их поменять местами и т.д.; правило 1 применяется столько раз, сколько возможно, т. е. пока не получится слово, в котором уже нет квадратика, расположенного левее кружочка, или в котором все кружочки лежат левее всех квадратиков; затем переходим к применению правила 2, а именно: если имеются два рядом стоящих кружочка, их удаляют, и правило 2 применяется столько раз, сколько возможно, т. е. пока не получится слово, в котором нет двух рядом стоящих кружочков; затем переходим к применению правила 3, а именно: если имеются два рядом стоящих квадратика, их удаляют, и это правило применяется столько раз, сколько возможно, т. е. пока не получится слово, в котором нет двух рядом стоящих квадратиков. Полученное слово является результатом преобразования исходного слова по заданным правилам и способу их применения, определяющим вместе некоторый алгоритм преобразования слов в данном алфавите.
На рисунки показано преобразование четырех слов по этому алгоритму.
Как показывает опыт обучения, повторив эту игру несколько раз для различных «слов», дети 5—6 лет в состоянии заранее правильно определить, какие вообще могут оказаться результаты сокращения «слов» по заданным правилам: кружочек и квадратик, или один кружочек, или один квадратик, или «ничего» (это «ничего» называют «пустым словом»).
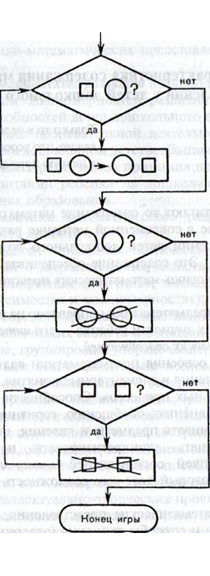Приведенные выше правила игры вместе с процедурой их применения могут быть изображены блок-схемой.
Умение применять разного рода алгоритмы, тем более умение предвидеть и обосновывать возможные результаты их применения — признак формирования свойственного для математика стиля мышления. Моделирование различных алгоритмов в виде детских игр открывает широкие возможности для формирования зачатков этого стиля мышления уже у дошкольников.
4. Моделирование как средство логико-математического развития детей дошкольного возраста
Согласно исследованиям, основы освоения моделирования закладываются в дошкольном возрасте, что вызывает пристальное внимание психологов и педагогов к генезису развития моделирования в дошкольном возрасте, разработке содержания моделей и технологий их использования в процессе освоения детьми различного содержания.
Особую роль играет моделирование в логико-математическом развитии детей. Математические понятия являются моделями разной степени условности (натуральный ряд чисел, планы, цифры и др.). Сложность их освоения обусловлена противоречием между образным мышлением дошкольника и абстрактностью самих понятий. В силу этого для детей дошкольного возраста необходима разработка и использование более наглядных моделей («модели нижнего яруса» по классификации В. А. Штоффа). Промежуточные модели, с одной стороны, способствуют развитию необходимых умений моделировать, с другой — представляют содержание в более упрощенной, доступной детскому восприятию и пониманию форме.
В современных исследованиях имеют место разные подходы к определению сущности моделирования.
• моделирование рассматривается как общелогический метод познания;
• как вид знаково-символической деятельности;
• как общая интеллектуальная способность.
Одна из наиболее распространенных классификаций моделей подразумевает деление на два основных класса: материальные модели, назначение которых состоит в физическом воспроизведении действительности, и идеальные модели, с которыми, даже при воплощении их в материале, все преобразования осуществляются мысленно (образные, знаковые). В психологических работах модель определяют как особый вид знака и моделирование трактуют как один из видов знаково-символической деятельности (ЗСД).
ЗСД представляется как особая деятельность со знаково-сим волическими средствами (ЗСС). Среди них выделяются схематизированные, в которых передана структура действительности (план комнаты и т. п.); знаковые, обозначающие содержание (формулы; знаки, обозначающие сложение, вычитание, умножение, деление; цифры и т. п.). Выделяют также две формы ЗСС: вещественную (специальный дидактический материал, например блоки Дьенеша, палочки Кюизенера) и графическую (схемы, таблицы).
Ребенку необходимо освоить соотнесение «обозначаемое — обозначающее», которое является сущностью семиотической функции. Семиотическая функция понимается как целостное образование, включающее различение «обозначаемого» (и в нем: предмет и знак) и «обозначающего» (форму и содержание); определение связи между ними.
Изучение психологических предпосылок овладения моделированием и его генезиса в дошкольном детстве привело к определению моделирования как общей интеллектуальной способности (Л.А. Венгер, Р. И. Говорова, О. М.Дьяченко, С.Л. Лоренсо, А. М. Сиверио и др.). В основе данной интеллектуальной способности лежит овладение детьми практическими действиями замещения, использования моделей, моделирования. Наглядное моделирование выступает средством ориентировки детей в действительности, обобщения, планирования и контроля действий и составляет одну из форм опосредования, которыми овладевают дошкольники. Л. А. Венгер отмечал, что наглядно-образное мышление дошкольников опосредуется наглядным моделированием, в котором в условно-семантической форме отражаются различного вида отношения. Источником развития моделирования является детская деятельность, которой свойственна моделирующая направленность.
Основываясь на идеях интериоризации внешних действий, в психологии экспериментально изучен генезис моделирования. Развиваясь на основе овладения действиями замещения (3—4 года), моделирование превращается в средство познания (4—6 лет) и далее, «присваиваясь» детьми, становится способом познания, собственно моделированием (6 лет и старше).
Особенности освоения замещения, моделирования в раннем и дошкольном возрасте. В процессе анализа особенностей опосредованного познания детьми свойств и отношений можно условно наметить две линии: развитие собственно моделирования и освоение содержания посредством использования модели (см. таблицу).
Младшие дошкольники могут применять самые простые сенсорные по содержанию и предметные по форме выражения модели (иконические) в процессе опосредованного познания свойств и отношений. В данном возрасте ценно именно непосредственное познание свойств и отношений. Осваиваются самые простые модели, обеспечивающие начальную систематизацию или дифференциацию сенсорных ощущений: геометрические фигуры, названия цветов, обозначение частей суток четырьмя разноцветными квадратами и т. п. При использовании модели детей привлекает сам способ замещения, а н