Геометрические приложения определенных интегралов
Теоретическое введение
С помощью определенного интеграла можно решить ряд геометрических задач.
6.1.1 Вычисление площадей плоских фигур
С помощью определенного интеграла можно найти площадь плоской области, ограниченной снизу и сверху двумя кривыми у = f 1(х), у = f 2(х) и f 1(x) ≤ f 2(x) при а ≤ х ≤ b, где f 1(x) и f 2(х) – две непрерывные функции (рис. 1). Площадь такой области равна:

| (1) |

Рис. 1
Формула (1) сохраняет свой вид и в случае, когда функции у = f 1(х), у = f 2(х) принимают отрицательные значения во всем интервале или в некоторой его части.
6.1.2 Вычисление объемов
Другой важной геометрической задачей, при решении которой используется определенный интеграл, является нахождение объёма тела.
Объем тела вращения вокруг оси Ох.
Пусть криволинейная трапеция, ограниченная графиком непрерывной неотрицательной функцией у = f (х) при a ≤ x ≤ b, прямыми х = a, х = b и осью Ох, вращается вокруг оси Ох. В этом случае объем тела вращения равен:

| (2) |
Объем тела вращения вокруг оси Оy.
Пусть теперь криволинейная трапеция, ограниченная графиком непрерывной неотрицательной функции у = f (х) при a ≤ x ≤ b, прямыми х = a, х = b и осью Ох, вращается вокруг оси Оy (а ≥ 0). Объем полученного тела вращения вычисляется по формуле:
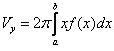
| (3) |
Замечание. При вращении вокруг оси Оу криволинейной трапеции, ограниченной двумя горизонтальными прямыми у = c, у = d, осью Оу и графиком функции х = φ (у), получим тело вращения, объём которого определяется по формуле (2), если поменять ролями х и у (c < d) (рис. 2):

| (4) |

Рис. 2
6.1.3 Длина дуги кривой
Другим важным применением определенного интеграла является вычисление длины дуги кривой, которая может быть задана в прямоугольных координатах с помощью функции у = f (x).
Пусть дуга кривой АВ задана уравнением у = f (х), a ≤ x ≤ b, А (a, f (a)), B (b, f (b)). Разобьём дугу на n произвольных частей точками M 0 = А, М 1, М 2,..., Мn = В с абсциссами а = х 0, x 1, x 2,..., хn = b, соединим эти точки хордами и получим некоторую ломаную линию M 0 M 1 M 2... Mn (рис. 3).
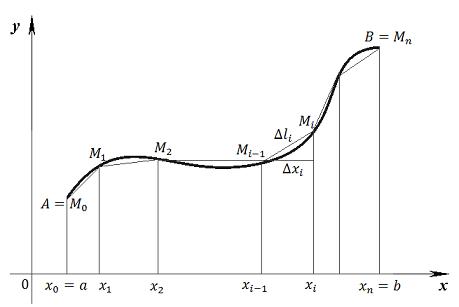
Рис. 3
Определение. Длиной lAB дуги АВ кривой называется предел последовательности длин ломаных при стремлении к нулю длины λ ее наибольшего звена, если этот предел существует, конечен и не зависит от способа разбиения кривой, т.е.
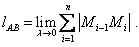
Сама кривая в этом случае называется спрямляемой.
Можно показать, что если функция f (х) непрерывна на отрезке [ a, b ] вместе со своей производной, то кривая АВ спрямляема. В этом случае вычислить длину дуги кривой у = f (х), х є [ a, b ] можно по формуле:
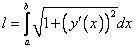
| (5) |
Содержание типового расчета
1. Вычислить площадь плоской фигуры, ограниченной заданными линиями.
2а. Вычислить объем тела, образованного вращением плоской фигуры, ограниченной заданными линиями, вокруг оси Ох.
2б. Вычислить объем тела, образованного вращением плоской фигуры, ограниченной заданными линиями, вокруг оси Оy.
3. Вычислить длину дуги заданной кривой.
Замечание. Студент получает задание типа 2а или 2б в зависимости от номера варианта.
Примеры выполнения типового расчета
Пример 1. Вычислить площадь, ограниченную параболой у = 3 х 2 + 2 х и прямой у = 3 х +2.
Решение. Сделаем чертеж плоской области D, ограниченной графиками функций y = 3 x 2 + 2 x и y = 3 x + 2 (рис. 4).

Рис. 4
Найдем точки пересечения параболы у = 3 х 2 + 2 х с осью Ох, тогда имеем:
у = 3 х 2 + 2 х = 0; => х (3 x + 2) = 0, х = 0 и x =  .
.
Найдем также точки пересечения параболы и прямой:
3 х 2 + 2 х = 3 х + 2; => 3 х 2 – х – 2 = 0; => x 1 =  , x 2 = 1 =>
, x 2 = 1 =>
y 1 = 3 x 1 + 2 = 0; y 2 = 3 x 2 + 2 = 5 => A (–2/3; 0), B (1; 5).
Так как коэффициент при х положителен, то ветви параболы направлены вверх. А прямую у = 3 х + 2 построим через две точки А (–2/3; 0) и В (1; 5) (рис. 4).
Используя формулу (1), вычислим площадь S плоской области:


Ответ: S 
Пример 2а. Вычислить объем тела, образованного вращением фигуры, ограниченной осью Ох, параболой y = 2 x 2 и прямой y = – x + 3 вокруг оси Ох.
Решение. Для построения чертежа найдем сначала абсциссы точек пересечения прямой и параболы (рис. 5), решая систему уравнений:

Второе решение х 2 = –3/2 не удовлетворяет условию задачи.
Поскольку верхняя граница фигуры составлена из двух различных линий, то объем искомого тела определим как сумму объемов тел вращения, образованных вращением вокруг оси Ох криволинейных трапеций, ограниченных:
1) кривой y 1 = 2 x 2, прямой х = 1 и осью абсцисс;
2) прямыми y 2 = 3 – x, х = 1 и осью абсцисс.

Рис. 5
Объемы этих тел вычисляем, используя формулу (2):
 ,
,
где нижнему пределу а первого интеграла соответствует х = 0 (точка пересечения параболы y = 2 x 2 и оси Ох), а верхнему пределу с второго интеграла соответствует х = 3 (точка пересечения прямой y = – x + 3 и оси Ох). Следовательно,

Ответ: 
Пример 2б. Вычислить объём тела, образованного вращением плоской области, ограниченной параболой y = x 2 – 6 x + 9 и прямой у = 4 х вокруг оси Оу.
Решение. Построим область, ограниченную параболой у = x 2 – 6 x + 9 и прямой у = 4 х (рис. 6). Так как у = x 2 – 6 x + 9 = (х – 3)2, то парабола касается оси Ох в точке С с абсциссой х = 3, ветви её направлены вверх. Найдем точки пересечения параболы с прямой:
 => x 2 – 6 x + 9 = 4 x =>
=> x 2 – 6 x + 9 = 4 x => 
Точки пересечения имеют координаты А (1, 4), В (9, 36). Эта плоская область D вращается вокруг оси Оу, получим тело вращения, изображенное на рис. 6.
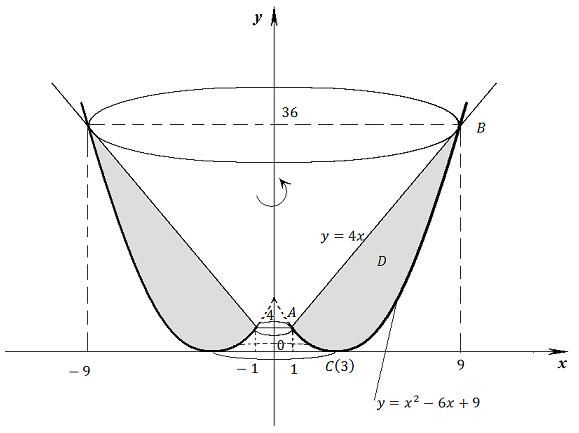
Рис. 6
Объём полученного тела вращения равен разности объёмов двух тел, полученных от вращения вокруг оси Оу двух криволинейных трапеций, заключенных между прямыми х = 1, х = 9 и осью Ох, одна из которых сверху ограничена прямой у = 4 х, а другая – параболой у = х 2 – 6 х + 9. Тогда по формуле (3):
 ≈ 2681.
≈ 2681.
Ответ:  ≈ 2681.
≈ 2681.
Пример 3. Вычислить длину дуги кривой  , если – 0.2 ≤ x ≤ 0.1.
, если – 0.2 ≤ x ≤ 0.1.
Решение. Для вычисления, длины дуги кривой  сначала найдем производную:
сначала найдем производную:
 .
.
Тогда 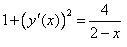 ,
,
и длина дуги равна, согласно формуле (5):

Ответ: l ≈ 0,419.
Оформление отчета
В отчете должны быть представлены все выполненные расчеты, по задачам 1 и 2 – аккуратно выполненные чертежи. Численные ответы должны быть получены с тремя значащими цифрами.