Тема 1.3. Теория пар сил
Пару сил в механике рассматривают как одно из основных понятий наряду с понятием силы. Действие пары сил на твердое тело определяется её моментом.
1.3.1. Пара сил и алгебраический момент пары сил
Парой сил называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны (рис. 1.9). Пара сил не составляет системы сил, эквивалентной нулю. Пару сил нельзя заменить одной силой, и, следовательно, она не имеет равнодействующей, а является такой системой сил, упростить которую нельзя. Каждая из сил, входящих в состав пары сил, имеет свойства обычных сил.
Пара сил, действующих на твердое тело, характеризуется прежде всего плоскостью действия – плоскость, в которой расположены силы пары.
Алгебраическим моментом пары сил называют взятое со знаком плюс или минус произведение одной их сил пары на плечо пары сил.
Плечом пары сил d называют кратчайшее расстояние между линиями действия сил пары (рис. 1.10).
Алгебраический момент пары обозначим M или 
. Согласно определению,
. (1.20)
| Рис. 1.10 |
Алгебраический момент пары сил имеет знак плюс, если пара сил стремится вращать тело против часовой стрелки, и знак минус, если пара сил стремится вращать тело по часовой стрелке.
Алгебраический момент пары сил численно равен площади параллелограмма, построенного на силах пары:
. (1.21)
1.3.2. Векторный момент пары сил
Пару сил, приложенную к твердому телу, можно охарактеризовать плоскостью действия, величиной момента пары сил и направлением вращения пары.
Векторным моментом пары сил назовем вектор, числовая величина которого равна произведению силы пары на ее плечо.
| Рис. 1.11 |
Векторный момент пары сил 
обозначим 
или . Согласно определению, числовое значение векторного момента пары сил 
совпадает с модулем алгебраического момента пары сил и, следовательно:
. (1.22)
Векторный момент пары сил можно выразить в виде векторного произведения двух векторов:
. (1.23)
1.3.3. Эквивалентность пар сил.
Две пары называют эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.
Приведем без доказательства три теоремы об эквивалентности пар сил и выводы, следующие из них.
Теорема 1. Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющей одинаковый с первой парой алгебраический момент.
Следствия из теоремы:
1. Пару сил, как жесткую фигуру, можно как угодно поворачивать и переносить в ее плоскости действия.
2. У пары сил можно изменять плечо и силы, сохраняя при этом алгебраический момент пары и плоскость действия.
Теорема 2. Пару сил, не изменяя ее действия на твердое тело, можно перенести из одной плоскости в другую, параллельную ей.
Теорема 3. Две пары сил, действующие на одно и то же твердое тело, эквивалентны, если они имеют одинаковые по модулю и направлению векторные моменты.
На основании приведенных теорем можно сделать заключение, что векторный момент пары сил, действующий на твердое тело, есть свободный вектор.
1.3.4. Теорема о сумме моментов сил пары
| Рис. 1.12 |
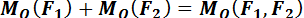, (1.24)
где O – любая точка.
Эту теорему докажем, вычисляя левую часть равенства (1.24):
, (1.25)
так как для пары сил
.
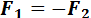Но
и не зависит от выбора точки O. Следовательно,
, (1.26)
что совпадает с векторным моментом пары сил . Таким образом,
. (1.27)
Взяв за точку O последовательно точки A и B, по формуле (1.24) имеем
, (1.28)
т. е. векторный момент пары сил равен векторному моменту одной из сил пары относительно точки приложения другой силы пары.
Эта теорема имеет важное значение при решении задач, когда надо вычислять сумму моментов сил пары относительно какой-либо точки.
Если моментная точка O выбирается в плоскости действия сил пары как частный случай, справедлива теорема о сумме алгебраических моментов сил пары: сумма алгебраических моментов сил, входящих в состав пары сил, относительно точки, лежащей в плоскости действия пары сил, равна алгебраическому моменту пары сил и, следовательно, не зависит от выбора моментной точки, т. е.
. (1.29)
Выбирая за моментные точки A и B, лежащие на линиях действия сил пары, получаем
, (1.30)
т. е. алгебраический момент пары сил равен алгебраическому моменту одной из сил пары относительно точки, лежащей на линии действия другой силы пары.
1.3.5. Сложение пар сил
Рассмотрим случай, когда пары сил не лежат в одной или параллельных плоскостях, а расположены в пересекающихся плоскостях. Докажем, что две пары сил, действующие на одно и то же тело и лежащие в пересекающихся плоскостях, можно заменить одной эквивалентной парой сил, векторный момент которой равен сумме векторных моментов заданных пар сил.
Пусть имеются две пары сил 
и 
(рис.1.13), лежащие в пересекающихся плоскостях. Эти пары сил можно получить из пар сил, как угодно расположенных в пересекающихся плоскостях, путем параллельного переноса, поворота в плоскости действия и одновременного изменения плеч и сил пар. Сложим силы в точках
Рис. 1.13 A и B по правилам параллелограмма. После сложения получим две силы 
и 
:
, 
. (1.31)
Силы и составляют пару сил, так как они приложены в разных точках и 
как равнодействующие равных, но противоположных сил, образующих пары сил.
Итак, при сложении двух пар сил, лежащих в пересекающихся плоскостях, получается эквивалентная пара сил. Обозначим векторный момент пары сил 
. Тогда
. (1.32)
Учитывая, что
, (1.33)
где 
и 
– векторные моменты заданных пар сил 
и 
, имеем
, (1.34)
т. е. векторный момент эквивалентной пары сил равен сумме векторных моментов заданных пар сил.
Таким образом, чтобы сложить две пары сил, лежащие в пересекающихся плоскостях, надо сложить их векторные моменты по правилу параллелограмма в какой-либо точке тела, например в точке B, как показано на рис. 1.13. Сложение пар сил, лежащих в одной плоскости и параллельных плоскостях, есть частный случай сложения пар сил в пересекающихся плоскостях, так как в этом случае их векторные моменты параллельны и, следовательно, векторное сложение перейдет в алгебраическое.
Последовательно применяя правило параллелограмма к каждым двум векторным моментам пар сил, можно любое количество пар сил в общем случае заменить одной парой сил, векторный момент которой равен сумме векторных моментов заданных пар сил:
; 
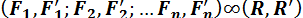(1.35)
1.3.6. Условия равновесия пар сил
Если на твердое тело действует пары сил, как угодно расположенные в пространстве, то эти пары сил можно заменить одной эквивалентной парой сил, векторный момент которой равен сумме векторных моментов заданных пар сил, т. е.
(1.36)
Для равновесия пар сил, действующих на твердое тело, необходимо и достаточно, чтобы модуль векторного момента эквивалентной пары сил равнялся нулю.
Итак, 
. Отсюда
(1.37)
Таким образом, для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций векторных моментов пар сил на каждую из трех координатных осей была равна нулю.
В общем случае пары сил можно уравновесить только парой сил и нельзя уравновесить одной силой или какой-либо другой системой сил, отличной от пары сил.
В случае, когда пары сил действуют на твердое тело, находясь в плоскости, их можно заменить одной эквивалентной парой сил, алгебраический момент которой равен сумме алгебраических моментов составляющих пар сил:
(1.38)
Для равновесия таких пар сил необходимо и достаточно, чтобы алгебраический момент эквивалентной им пары сил был равен нулю, т. е. для равновесия пар сил, действующих на твердое тело в одной плоскости, необходимо и достаточно, чтобы сумма алгебраических моментов этих пар сил была равна нулю.
Тема 1.4. Приведение произвольной системы сил
При изучении произвольной системы сил рекомендуется найти метод, позволяющий перенести все силы в одну точку (метод Пуансо).
1.4.1. Приведение силы к заданному центру
| Рис. 1.14 |
Силу можно переносить параллельно самой себе в любую точку твердого тела, добавляя при этом пару сил, векторный момент которой равен векторному моменту переносимой силы относительно новой точки приложения силы.
Пусть имеем силу 
, приложенную к твердому телу в точке A (рис. 1.14). Приложим в точке тела B, выбранной за центр приведения, систему двух равных по модулю, но противоположных по направлению сил 
и 
, параллельных заданной силе . Силы и составляют систему сил, эквивалентную нулю, и ее можно добавить к любой заданной системе сил. Пусть по модулю
,
тогда
.
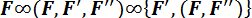Система двух равных по модулю и противоположных по направлению параллельных сил 
составляет пару сил, которую называют присоединенной парой сил.
Итак, вместо силы , приложенной в точке A, получены сила 
, равная ей по модулю и направлению, но приложенная в точке B, и присоединенная пара сил , векторный момент которой
. (1.39)
Процесс замены силы силой и парой сил называют приведением силы к заданному центру В.
1.4.2. Главный вектор и главный момент системы сил
Главным вектором системы сил называют вектор, равный векторной сумме этих сил (рис. 1.15):
Рис. 1.15
геометрически изображается замыкающим вектором силового многоугольника, построенного на заданных силах. Проецируя обе части векторного равенства (1.40) на координатные оси, для произвольной пространственной системы сил, получаем
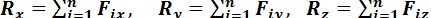(1.41)
По проекциям определяют модуль главного вектора и косинусы его углов с осями координат:
,
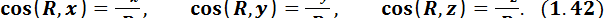
Главным моментом системы сил относительно точки О тела называют сумму векторных моментов всех сил системы относительно этой точки:
Главный момент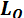 
геометрически изображается замыкающим вектором многоугольника, построенного на векторных моментах сил относительно центра приведения. Проецируя обе части векторного равенства (1.43) на прямоугольные оси координат и используя связь момента силы относительно оси с проекцией векторного момента этой силы относительно оси с проекцией векторного момента этой силы относительно точки на оси, имеем:
Модуль главного момента и косинусы его углов с осями координат равны:
1.4.3. Приведение произвольной системы сил
к силе и паре сил
Докажем основную теоремы статики (теорему Пуансо).
Любую произвольную систему сил, действующих на твердое тело, можно в общем случае привести к силе и паре сил.
Процесс замены системы сил одной силой и парой силназывают приведением системы сил к заданному центру.
Пусть дана произвольная система сил 
приложенных к твердому телу. Выберем произвольную точку O тела за центр приведения и каждую силу заданной системы сил приведем к точке О. Получим
.
Таким образом, система из n сил заменена системой из 3n сил, т. е. в точке О приложена система сходящихся сил 
и на твердое тело действует также система и присоединенных пар сил:
.
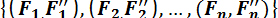Векторные моменты присоединенных пар сил можно выразить через векторные моменты заданных сил:
Рис. 1.16
Систему сходящихся сил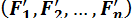 
заменим их равнодействующей , которая равна векторной сумме сил 
и геометрически изображается замыкающим вектором силового многоугольника, построенного на этих силах (рис. 1.16).
Итак,
(), (1.47)
где
Для заданно системы сил является лишь только ее векторной суммой, или главным вектором. Систему присоединенных пар с 
по теореме о сложении пар сил можно заменить одной парой сил с векторным моментом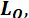 
который является главным моментом. Главный момент 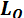равен сумме векторных моментов присоединенных пар. Учитывая формулу (1.48) для 
имеем
(1.49)
Индекс «О» у 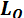– означает, что за центр приведения взята точка О.
Таким образом, доказана основная теорема статики.
Любую систему сил, действующих на твердое тело, можно привести к силе, приложенной в центре приведения, равной главному вектору системы сил, и паре сил, векторный момент которой равен главному моменту системы сил относительно точки, выбранной за центр приведения.
В краткой форме эту теорему можно выразить так:
. (1.50)
1.4.4. Условия равновесия системы сил
1. Условия равновесия системы сил в векторной форме. Очевидно, что если система сил находится в равновесии, то в равновесии находится и эквивалентная ей система, состоящая из силы и пары сил. Для равновесия системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор системы был равен нулю и главный момент системы сил относительно любого центра приведения также был равен нулю. Иначе для того чтобы 
, необходимы и достаточны условия
(1.51)
Условия (1.51) являются векторными условиями равновесия для любой системы сил.
2. Условия равновесия пространственной системы сил в аналитической форме. Если при равновесии системы сил, приложенных к твердому телу, главный вектор 
равен нулю, то его проекция на каждую координатную ось также равна нулю. Это справедливо и для главного момента. Таким образом, из векторных условий равновесия пространственной системы силы следует шесть условий:
(1.52)
Учитывая формулы (1.41) и (1.44), эти шесть условий через силы системы выражаются в форме
(1.53)
Таким образом, для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы три суммы моментов всех сил относительно трех осей координат также были равны нулю.
3. Условия равновесия плоской системы сил. Плоской системой сил, приложенных к твердому телу, называют такую систему сил, линии действия которых лежат в одной плоскости.
Основная теорема статики справедлива для любой системы сил, в том числе и для плоской.
| Рис. 1.17 |
и 
в плоскости действия сил (рис. 1.17). Так как ось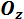 
перпендикулярна силам, то 
выполняется для всех плоских систем сил, т. е. является тождеством. Каждая из сил расположена в одной плоскости с осями координат 
, и поэтому их моменты относительно этих осей равны нулю. Таким образом, условия равновесия становятся тождествами, т.е.
(1.54)
Моменты сил относительно оси 
, перпендикулярной силам, равны алгебраическим моментам этих сил относительно точки О. Таким образом,
(1.55)
Для плоской системы сил после отбрасывания тождеств (1.54) имеем следующие три условия равновесия:
Условия равновесия (1.56) назовем условиями равновесия плоской системы сил в первой форме.
Условия равновесия плоской системы сил, приложенных к твердому телу, можно сформулировать в других эквивалентных формах. Существуют еще две формы необходимых и достаточных условий равновесия.
Рассмотрим эти условия равновесия в виде теоремы о трех моментах и третьей формы условия равновесия.
· Теорема о трех моментах (вторая форма условий равновесия). Для равновесия плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы алгебраических моментов сил системы относительно трех любых точек расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю, т. е.
· Третья форма условий равновесия. Для равновесия плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы сумма алгебраических моментов сил относительно двух любых точек, лежащих в плоскости действия сил, были равны нулю и алгебраическая сумма проекций этих сил на какую – либо ось плоскости, не перпендикулярную прямой, проходящей через две моментальные точки, также была равна нулю, т. е.
(1.58)
где за ось x принята любая прямая, не перпендикулярная AB.
4. Условия равновесия сходящейся системы сил. Системой сходящихся сил (или пучком сил) называют такую систему сил, линии действия которых пересекаются в одной точке, центре пучка (рис. 1.18). Сходящиеся системы сил могут быть пространственными и плоскими.
Если за моментную точку выбрать точку O, то главный момент 
тождественно. Тогда условия равновесия (1.53) принимают вид
(1.59)
Для плоской системы сходящихся сил, расположенной в плоскости 
, уравнение 
выполняется тождественно и условия равновесия имеют вид
(1.60)
| Рис. 1.18 |
Тема 1.5. Частные случаи пространственных систем
Пространственная система сил является наиболее общим случаем действия сил на твердое тело, позволяющая выделить частные варианты, определить схему взаимодействия сил и структуру формул.
1.5.1. Изменение главного момента при перемене
центра приведения
При перемене центра приведения векторные моменты сил изменяются, так как изменяются радиус-векторы точек приложения. Вследствие этого изменяется главный момент. Оценим изменение главного момента системы сил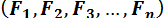 
. Пусть система сил приведена к центру O и получены в этой точке главный вектор и главный момент 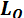(рис. 1.19). Выберем в качестве центра приведения другую точку 
и вычислим главный момент 
рассматриваемой системы сил.
Так как
, (1.61)
то для получения главного момента достаточно привести к новому центру систему 
. Силу из точки О переносим в точку . Получим в этой точку силу 
и согласно теореме о параллельном переносе силы, присоединенную пару сил с векторным моментом 
. Векторный момент пары сил 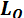, вычисленный относительно точки O как вектор свободный, можно приложить в любой точке тела. Новый главный момент относительно точки по правилу сложения пар сил является векторной суммой моментов 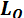и , т. е.