Вычисление статических характеристик.
При проведении испытаний образцов бетона на прочность после пропарки получены следующие результаты:
| 295.6 | 188.7 | 242.3 | 271.7 | 256.7 | 192.1 | 165.9 | 232.8 | 245.6 | 223.6 |
| 256.1 | 245.7 | 274.6 | 246.5 | 212.5 | 201.5 | 183.0 | 148.8 | 299.5 | 306.0 |
| 188.7 | 193.0 | 261.7 | 250.8 | 281.4 | 274.8 | 223.6 | 232.6 | 306.0 | 243.5 |
| 252.6 | 280.5 | 250.2 | 299.2 | 249.1 | 288.2 | 220.2 | 193.0 | 238.2 | 280.5 |
| 225.3 | 287.0 | 275.4 | 240.6 | 282.2 | 223.0 | 260.4 | 242.3 | 219.3 | 300.1 |
| 205.7 | 207.8 | 211.1 | 262.7 | 226.1 | 260.1 | 173.4 | 176.0 | 195.5 | 203.2 |
| 304.3 | 260.9 | 200.9 | 212.5 | 256.7 | 274.6 | 190.4 | 272.3 | 299.5 | 179.9 |
| 278.8 | 272.0 | 238.0 | 215.1 | 255.3 | 173.4 | 273.6 | 222.9 | 211.1 | 172.6 |
| 252.5 | 210.0 | 250.2 | 181.1 | 242.3 | 182.8 | 257.0 | 208.3 | 299.5 | 272.3 |
| 136.0 | 289.0 | 277.1 | 243.4 | 306.0 | 147.8 | 222.9 | 306.0 | 242.3 | 181.1 |
| 181,1 | 200,9 | 212,5 | 226,1 | 243,4 | 252,6 | 262,7 | 277,1 | 299,2 | |
| 147,8 | 182,8 | 201,5 | 215,1 | 232,6 | 243,5 | 255,3 | 271,7 | 278,8 | 299,5 |
| 148,8 | 203,2 | 219,3 | 232,8 | 245,6 | 256,1 | 280,5 | 299,5 | ||
| 165,9 | 188,7 | 205,7 | 220,2 | 245,7 | 256,7 | 272,3 | 280,5 | 299,5 | |
| 172,6 | 188,7 | 207,8 | 222,9 | 238,2 | 246,5 | 256,7 | 272,3 | 281,4 | 300,1 |
| 173,4 | 190,4 | 208,3 | 222,9 | 240,6 | 249,1 | 273,6 | 282,2 | 304,3 | |
| 173,4 | 192,1 | 242,3 | 250,2 | 260,1 | 274,6 | ||||
| 211,1 | 223,6 | 242,3 | 250,2 | 260,4 | 274,6 | 288,2 | |||
| 179,9 | 211,1 | 223,6 | 242,3 | 250,8 | 260,9 | 274,8 | |||
| 181,1 | 195,5 | 212,5 | 225,3 | 242,3 | 252,5 | 261,7 | 275,4 | 295,6 |
Определить закон распределения случайной величины Х – прочности бетона после пропарки.
Чтобы выдвинуть гипотезу о законе распределения случайной величины, в нашем примере прочности бетона, нужно построить эмпирическую кривую. Для этого легче всего воспользоваться гистограммой. Вычислим возможную длину интервала h по формуле:
h = 22, тогда k – количество интервалов:
| h= | |
| k= |
Найдем a0 – левый конец первого интервала. Он берется таким, чтобы хmin лежало внутри первого интервала:
А уже а1 = а0 + h
Количество интервалов получается так:
Теперь расположим статистические данные по интервалам, а в каждом интервале укажем частоту – количество вариантов, попадающих в данный интервал.
| Интервал | mi |
| (125;147) | |
| (147;169) | |
| (169;192) | |
| (192;214) | |
| (214;236) | |
| (236;258) | |
| (258;281) | |
| (281;303) | |
| (303;325) |
Вычисляем относительные частоты 
и 
| 
|
| 0,01 | 0,00045 |
| 0,03 | 0,001349 |
| 0,12 | 0,005396 |
| 0,15 | 0,006745 |
| 0,12 | 0,005396 |
| 0,23 | 0,010342 |
| 0,18 | 0,008094 |
| 0,11 | 0,004946 |
| 0,05 | 0,002248 |
Графическое изображение вариационного ряда позволяет представить в наглядной форме закономерности изменения варианты. Наиболее широко используется гистограмма, полигон.
Полигон, как правило, служит для изображения дискретного вариационного ряда. Для его построения в прямоугольной системе координат наносятся точки с координатами (х; 
), где х – варианта, а - ее частота. Но 
может быть большим числом, поэтому его заменяют относительной частотой 
: 
причем, откладывается на оси OY, а х на оси OX. Построенные таким образом точки соединяются ломанной кривой. Эта ломанная кривая называется полигон.
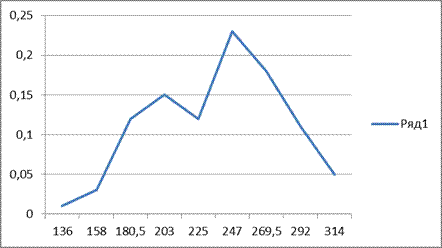
Теперь, чтобы сделать заключение об эмпирическом законе распределения построим гистограмму. Для этого на оси ОХ откладываем интервалы, а по оси ОY - .
Эту гистограмму можно считать эмпирической кривой распределения прочности бетона и можно выдвинуть гипотезу о нормальном распределении исследуемой случайной величины – прочности.
Проверка гипотезы о законе распределения.
Так как мы предположили, что исследуемая случайная величина распределена по нормальному закону, плотность которого имеет вид:
Этот закон имеет два параметра: α – математическое ожидание,
σ – среднее квадратическое отклонение.
Необходимо по составленному интервальному ряду найти оценки этих параметров, а потом с помощью какого-либо критерия согласия проверить правдоподобие нашей гипотезы. С этой целью составим таблицу:
| Интервал | Частота 
| 
| 
| 
| 
|
| (125;147) | -102,35 | 10475,5225 | 10475,5225 | ||
| (147;169) | -80,35 | 6456,1225 | 19368,3675 | ||
| (169;192) | 180,5 | -57,85 | 3346,6225 | 40159,47 | |
| (192;214) | -35,35 | 1249,6225 | 18744,3375 | ||
| (214;236) | -13,35 | 178,2225 | 2138,67 | ||
| (236;258) | 8,65 | 74,8225 | 1720,9175 | ||
| (258;281) | 269,5 | 31,15 | 970,3225 | 17465,805 | |
| (281;303) | 53,65 | 2878,3225 | 31661,5475 | ||
| (303;325) | 75,65 | 5722,9225 | 28614,6125 | ||
| ∑ | 31352,5025 | 170349,25 |
a = 
238,35
σ= 
41
Итак, эмпирическая функция распределения имеет плотность распределения:
А соответствующий закон распределения F(x):
А теперь посчитаем теоретические вероятности попадания случайной величины в интервал (хi, хi+1) по формуле:
,
Где Ф(х) – функция Лапласа.
| (xi;xi+1) | P(α<x<β) | 
|
| (125;147) | Ф(2,74)-Ф(2,20)= | 0,0108 |
| (147;169) | Ф(2,20)-Ф(1,66)= | 0,0346 |
| (169;192) | Ф(1,66)-Ф(1,13)= | 0,0807 |
| (192;214) | Ф(1,13)-Ф(0,59)= | 0,1484 |
| (214;236) | Ф(0,59)-Ф(0,05)= | 0,2025 |
| (236;258) | Ф(0,48)+Ф(0,05)= | 0,2043 |
| (258;281) | Ф(1,02)-Ф(0,48)= | 0,1617 |
| (281;303) | Ф(1,55)-Ф(1,02)= | 0,0933 |
| (303;325) | Ф(2,09)-Ф(1,55)= | 0,0427 |
| ∑ | 0.979  1
|
Теперь проверим на сколько предполагаемый закон распределения исследуемой случайной величины (эмпирический) близко подходит к теоретическому. Для этого нужно составить случайную величину χ² по следующей формуле:
,
Где k = 9 – число интервалов, Рi – вычисленные теоретические вероятности, n = 100.
|
| 0,00592593 |
| 0,06115607 |
| 1,91386617 |
| 0,00172507 |
| 3,36111111 |
| 0,32329418 |
| 0,20710575 |
| 0,29891747 |
| 0,12480094 |
Таким образом:
| 6,29790268 |
| 12.6 |
Сравниваем χ²набл. с теоретическим, при условии что α = 0,05, а r – число степеней свободы равно r = 9 – 3 = 6. Получаем что 6,29790268>12.6 следовательно нет оснований отвергать гипотезу о нормальном распределении случайной величины