Задачи с нелинейными ограничениями-неравенствами

Теория

Типичная стратегия в алгоритмах возможных направлений заключается в следующем. На каждой итерации метода строится возможное направление спуска и затем проводится оптимизация вдоль этого направления. Возьмем допустимую точку x_k и найдем направление спуска d_k такое, что для достаточно малых l > 0 выполняются следующие требования: точка x_k + l d_k допустимая и значение целевой функции в точке x_k + l d_k лучше, чем в x_k. После нахождения такого направления решается задача одномерной минимизации, чтобы определить, как далеко следует двигаться вдоль d_k. Это приводит в новую точку x_{k + 1}, и процесс повторяется. Определение 8.1 вводит понятие возможного направления спуска.

Определение 8 .1. Рассмотрим задачу минимизации f (x) при условии, что x Î S, где f: E_n ® E ₁, а S - непустое множество из E_n. Ненулевой вектор d называется возможным направлением в точке x Î S, если существует такое d > 0, что x + l d Î S для всех l Î (0, d). Вектор d называется возможным направлением спуска в точке x Î S, если существует такое d > 0, что f (x + l d) < f (x) и x + l d Î S для всех l Î (0, d).

.Случай линейных ограничений

Вначале рассмотрим случай, когда допустимая область S определена системой линейных ограничений, так что рассматриваемая задача имеет вид

Минимизировать f (x) при условиях Ax £ b, G x = c.

Здесь A – матрица порядка m ´ n, G – матрица порядка l ´ n, b есть
m -мерный вектор, а c есть l -мерный вектор.

Лемма 8.1. Рассмотрим задачу минимизации f (x) при условиях
A x £ bи Gx = c. Пусть x — допустимая точка, и предположим, что A ₁ x = b ₁ и A ₂ x < b ₂, где , . Тогда ненулевой вектор d является возможным направлением в точке x в том и только том случае, если A ₁ d £ 0 и Gd = 0. Если, кроме того, Ñ f (x) ^Td < 0, то d является возможным направлением спуска.

Лемма 8.2. Рассмотрим задачу минимизации f (x) при условиях
Ax £ b и Gx = c. Пусть x – допустимая точка, для которой A ₁ x = b ₁ и A ₂ x < b ₂, где 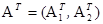, 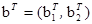. Тогда x является точкой Куна – Таккера в том и только том случае, если оптимальное значение целевой функции в задачах Р1, Р2 или Р3 равно нулю.

в задачу должно быть включено условие, которое ограничивало бы вектор d или оптимальное значение целевой функции. Такое ограничение обычно называют нормирующим. Ниже приведены три задачи построения возможного направления спуска. В каждой из этих задач используются различные формы нормировки.

Задача Р1:

минимизировать Ñ f (x) ^T d

при условиях A ₁ d £ 0, Gd = 0, –1 £ d_i £ 1, i = 1, …, n.

Задача Р2:

минимизировать Ñ f (x) ^T d

при условиях A ₁ d £ 0, G d = 0, d^T d £ 1.

Задача Р3:

минимизировать Ñ f (x) ^T d

при условиях A ₁ d £ 0, G d = 0, Ñ f (x) ^T d ³ –1.

Алгоритм метода Зойтендейка для случая линейных ограничений

Ниже приведен алгоритм метода Зойтендейка для минимизации дифференцируемой функции f при условии, что A x £ b и G x = c.

Начальный этап. Найти начальную допустимую точку x ₁, для которой
A x ₁ £ b и G x ₁ = c. Положить k = 1 и перейти к основному этапу.

Основной этап

Шаг 1. Пусть задана точка x_k. Предположим, что 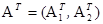и 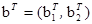, так что A ₁ x_k = b ₁ и A ₂ x_k < b ₂. Взять в качестве d_k оптимальное решение следующей задачи:

минимизировать Ñ f (x_k) ^T d при условиях

A ₁ d £ 0, G d = 0, –1 £ d_j £ 1, j = 1, …, n.

Если Ñ f (x_k) ^T d_k = 0, то остановиться; x_k – точка Куна – Таккера. В противном случае перейти к шагу 2.

Шаг 2. Положить l _k равным оптимальному решению следующей задачи линейного поиска:

минимизировать f (x_k + l d_k) при условии 0 £ l £ l_max,

где l_max определяется в соответствии с (5.1).

Положить x_{k +1} = x_k +l _kd_k, определить новое множество активных ограничений в x_{k +1} и переопределить A ₁ и A ₂. Заменить k на k +1 и перейти к шагу 1.

Задачи с нелинейными ограничениями-неравенствами

Теперь рассмотрим задачу, в которой допустимая область задается системой ограничений-неравенств, необязательно линейных:

минимизировать f (x) при условиях g_i (х) ≤ 0, i = 1 ,..., m.

Теорема 8.1. Рассмотрим задачу минимизации f (x) при условиях
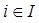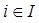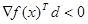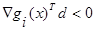g_i (x) ≤ 0 для i = 1, …, m. Пусть х – допустимая точка, а I – множество индексов активных в этой точке ограничений, т.е. I = { i: g_i (x) = 0}. Кроме того, предположим, что функции f и g_i для дифференцируемы в точке х, а функции g_i для непрерывны в этой точке. Если и при 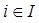, то вектор d является возможным направлением спуска.

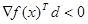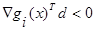Для того чтобы найти вектор d, удовлетворяющий неравенствам и для 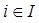, естественно минимизировать максимум из и для 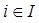. Обозначим этот максимум через z. Вводя нормирующие ограничения –1 ≤ d_i ≤ 1 для каждого j, получим следующую задачу для нахождения направления:

минимизировать z

при условиях (8.2)

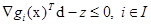, (8.3)

–1 ≤ d_i ≤ 1, j = 1, …, n. (8.4)

Пусть — оптимальное решение этой задачи линейного программирования. Если , то очевидно, что 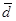— возможное направление спуска. Если же 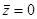то, как показано ниже, текущая точка является точкой Ф. Джона.

Теорема 8.2. Рассмотрим задачу минимизации f (x) при условиях
g_i (x) ≤ 0, i = l,..., т. Пусть х – допустимая точка, а I = { i: g_i (x) = 0}. Рассмотрим следующую задачу нахождения направления спуска:

минимизировать z при условиях (8.2) – (8.4).

Точка х является точкой Ф. Джона для исходной задачи тогда и только тогда, когда оптимальное значение целевой функции задачи поиска направления равно нулю.