Ряд Фурье для периодических функций.

Лекция 35. Тригонометрический ряд. Разложение функций в тригонометрический ряд Фурье (2ч)

 

Содержание лекции: Тригонометрический ряд Фурье. Разложение функции в тригонометрический ряд. Теорема Дирихле. Ряд Фурье для четных, нечетных функций, ряд Фурье для непериодических функций. Примеры.

Доказательство свойств тригонометрической системы.

Основные определения

Среди различных аналитических аппаратов, служащих орудиями исследования функций, первое место по своей простоте, гибкости, прозрачности, удобству употребления занимают функциональные ряды. Идея этого аппарата проста: исследуемая функция представляется как предел последовательности более простых и доступных исследованию функций – частичных сумм изображающего функцию ряда. Если такая частичная сумма на рассматриваемом промежутке достаточно близка к изучаемой функции (ряд сходится к этой функции), то можно рассчитывать, что свойства этой суммы достаточно точно описывают свойства изучаемой функции.

Какие же функции удобнее и выгоднее использовать в качестве элементов разложения? На этот вопрос нельзя дать единого универсального ответа, здесь все зависит от природы изучаемой функции и характера тех задач, которые мы по отношению к ней ставим.

Но существует несколько важнейших типов функциональных рядов, которые зарекомендовали себя в этом плане наилучшим образом. К ним относятся, в первую очередь, степенные ряды (, члены – неотрицательные степени независимой переменной) и тригонометрические ряды, изучением которых мы и займемся.

Определение 1.1.

Ряд вида

(1)

называется тригонометрическим рядом, числа - коэффициенты этого ряда, а отдельные слагаемые называются членами ряда или его гармониками.

Если степенной ряд построен по системе простых, хорошо изученных степенных функций 1, х, х ², х ³, …, хⁿ, …, то тригонометрический ряд построен с помощью системы тоже не менее хорошо изученных тригонометрических функций:

1, sin x, cos x, sin2 x, cos 2 x, sin 3 x, cos 3 x, …, sin nx, cos nx, …

– эта совокупность функций называется тригонометрической системой функций. Все функции системы имеют общий период и обладают следующими свойствами:

1) интеграл по отрезку (и любому другому отрезку длины 2π) от произведения любых двух функций этой системы равен нулю:

;

;

;

, ;

, ;

2) интеграл по отрезку от квадратов функций этой системы не равен нулю:

;

, ;

, .

Доказательство этих свойств рекомендуем провести самостоятельно.

Свойств 1 системы {1; cos nx, sin nx }, n Î N – называется свойством ортогональности, оно лежит в основе всей теории тригонометрических рядов.

Таким образом, тригонометрический ряд – это ряд, построенный по ортогональной тригонометрической системе функций.

Так как тригонометрический ряд – это функциональный ряд, то можно говорить о его области сходимости и сумме.

Если он сходится, то его сумма есть периодическая функция с периодом 2 p. Возникают естественные вопросы (как и в случае ряда Тейлора):

1) Какие функции можно разлагать в тригонометрический ряд, и на каких множествах?

2) Как разлагать (как найти коэффициенты)?

3) Единственно ли разложение?

Справедлива

Теорема 1.1. (необходимое условие разложимости в тригонометрический ряд).

Если функция f (x), интегрируемая на отрезке , разлагается на этом отрезке в почленно интегрируемый тригонометрический ряд, то есть

f (x) = , (2)

то это разложение единственно и коэффициенты ряда вычисляются по формулам:

n = 1, 2, … (3)

 

Доказательство. Пусть интегрируемая функция f (x) представима на отрезке [–p;p] тригонометрическим рядом:

. (2)

Проинтегрируем обе части этого равенства по x Î [ -p, p ]

.

В силу только что доказанных свойств системы {1, cos nx, sin nx }, интегралы, стоящие под знаком суммы, равны нулю.

Тогда .

Умножив обе части равенства (2) на cos nx и вновь проинтегрировав, получим

.

Опять же по свойствам ортогональной системы, справа только одно слагаемое при k = n отлично от 0, следовательно

Þ .

Аналогично, умножая (2) на sin nx и интегрируя, получаем:

.

Откуда .

Таким образом, если -периодическая функция f (x) разлагается в тригонометрический ряд (2), то его коэффициенты могут быть найдены по формулам

, , .

Причем, поскольку интегралы вычисляются однозначно, то ряд с такими коэффициентами – единственный. Что и требовалось доказать.

Определение 1. 3.

Коэффициенты тригонометрического ряда, вычисленные по формулам (3) называются коэффициентами Фурье, а тригонометрический ряд с такими коэффициентами называется рядом Фурье функции f (x).

Из Теоремы 1.1 следует: если f(x) разлагается в тригонометрический ряд, то это необходимо есть ряд Фурье этой функции.

Замечание:

Мы рассматривали интегралы по отрезку [ -p, p ], но если f (x) - -периодическая функция, то

" а.

То же касается и функций f (x)cos nx, f (x)sin nx. Значит, формулы (3) могут быть распространены на любой отрезок длины 2 p:

n = 0, 1, 2, … (3¢)

Ряд Фурье для периодических функций.

Теорема 1.1 ответила на последние два поставленных нами вопроса: как разложить и единственно ли разложение?

Осталось выяснить вопрос, какие функции можно разлагать, и при каких условиях формально построенный для функции ряд Фурье сходится именно к этой функции?

Ответ на этот вопрос дает Теорема Дирихле – достаточное условие разложимости в тригонометрический ряд.

Теорема 1.2. (Дирихле)

Пусть f (x) – -периодическая функция и на отрезке [ -p, p ] удовлетворяет условиям:

1) f (x) ограничена и непрерывная (кусочно-непрерывная),

2) f (x) кусочно-монотонная.

Тогда ряд Фурье этой функции сходится на всей числовой прямой, причем сумма ряда равна f (x) в точках непрерывности функции и равна в точках х ₀ разрыва функции.

Условия 1) – 2) Теоремы называются условиями Дирихле. Эти условия, очевидно, менее жесткие, нежели требование $-я производных всех порядков, которые позволяют разлагать функцию в ряд Тейлора. Значит, разложению в ряд Фурье может быть подвергнут более широкий класс функций.

Кроме того, члены ряда Фурье – периодические, волнообразные функции, а в различных областях человеческого знания (физике, механике, биологии, экономике) процессы часто носят периодический характер. Поэтому описание этих процессов с помощью ряда Фурье, безусловно, предпочтительнее.

Но не всякая периодическая функция имеет период . Оказывается, можно распространить рассмотренную теорию на функции с произвольным периодом. В случае если функция f (x) – 2 l -периодическая функция, то ряд Фурье имеет вид

(4)

с коэффициентами:

, n = 0, 1, 2, … (5)

При этом теорема Дирихле формулируется так:

Теорема (Дирихле):

Если 2l -периодическая функция на [ -l, l ] удовлетворяет условиям Дирихле, то ее ряд Фурье (4) сходится на всей числовой прямой, и его сумма равна f (x) в " точке непрерывности функции, а в " точке х ₀ разрыва функции сумма ряда равна .

Из Теоремы Дирихле следует, что для того, чтобы разложить периодическую с периодом Т=2 l функцию в тригонометрический ряд (ряд Фурье), нужно:

1) проверить монотонность, ограниченность, непрерывность (кусочную непрерывность) функции на заданном отрезке;

2) вычислить коэффициенты Фурье по формулам (5);

3) построить с этими коэффициентами ряд (4);

4) указать область сходимости ряда к функции.

Для ускорения процесса вычисления коэффициентов разложения рекомендую использовать таблицы интегралов (например, Двайта), в частности, такие формулы

, ,

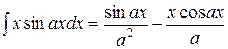а также учесть, что cos p n = (–1) ^п, sin p n = 0 " n ÎN.

Пример:

Рассмотрим -периодическую функцию, заданную на [ -p, p) условиями:

График этой функции:

 

 

Условия Дирихле, очевидно, выполняются, значит, ряд Фурье сходится к " х ¹ p (2 n +1).

Найдем коэффициенты разложения:

.

Тогда справедливо разложение

" х ¹ p (2 n +1), n Î Z;

при х = p (2 n +1) имеем сумму ряда S (x) = , что, очевидно, не совпадает со значением функции в этих точках.

Замечание.

В силу свойства интегралов от периодичных функций

–

2 l -периодическая функция может быть задана не только на отрезке [ -l; l ], а на " другом отрезке [ a, b ] длины 2 l. Более того, при необходимости от отрезка [ -l; l ] можно перейти к " другому отрезку такой же длины, например, к отрезку [0; 2 l ], в формулах коэффициентов при этом нужно лишь изменить пределы интегрирования. При таком переходе только нужно внимательно следить за описанием (аналитическим заданием) функции.

Например: , f (x) = f (x +2)

 

 

 

Очевидно

Процедуру разложения функции в тригонометрический ряд и изучение свойств этого ряда называют гармоническим анализом.