 (1). Ур-е вольтера – частный случай ур-я Фредгольма. Покажем, что ур-е Вольтера разрешимо при любых знач-х
(1). Ур-е вольтера – частный случай ур-я Фредгольма. Покажем, что ур-е Вольтера разрешимо при любых знач-х  . K(t,s), f(t) – непрер.,
. K(t,s), f(t) – непрер.,  .
. 
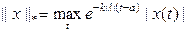 . Очевидно, что
. Очевидно, что  нормы эквив-ны. Обозначим
нормы эквив-ны. Обозначим  пр-во непрер. ф-ций с нормой
пр-во непрер. ф-ций с нормой  . Рассм.
. Рассм.  Можно показать, что
Можно показать, что  . Проверим усл-е сжатия:
. Проверим усл-е сжатия: 



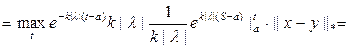


 Поскольку нер-во вып-ся вседа, то ур-е Вольтера всегда разрешимл и его м. решать методом посл. приближений.
Поскольку нер-во вып-ся вседа, то ур-е Вольтера всегда разрешимл и его м. решать методом посл. приближений.

 8. ГП. Пр. Н-во К-Б-Ш. Непрер-ть скал. произвед-я. Т.Пифагора. Ортогональность.
8. ГП. Пр. Н-во К-Б-Ш. Непрер-ть скал. произвед-я. Т.Пифагора. Ортогональность.
Пусть Н-ЛП. Н н-ся предгильбертовым или пр-вом со скал-м произвед-м, если  определено число (x,y) называемое скал-м произв-м так, что выполнены аксиомы: 1.
определено число (x,y) называемое скал-м произв-м так, что выполнены аксиомы: 1. 
 2.
2.  3.
3.  4.
4.  . Замечание. Из (2) => что
. Замечание. Из (2) => что 
Скалярное произвед-е порождает норму по ф-ле 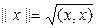
Первые аксиомы очевидны, нер-во треуг-ка следует из Нер-ва Шварца: 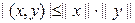 Д-во:
Д-во: 
 Пусть
Пусть  и
и  ,
,  ,
,  Нер-во Шварца. Проверим нер-во треуг-ка:
Нер-во Шварца. Проверим нер-во треуг-ка: 


Предгильбертово пр-во полное, относительно нормы, порожденной скал. произвед-м н-ся гильбертовым.
Утверждение. Скал-е произвед-е есть непрер-я ф-ция своих аргументов. Д-во: 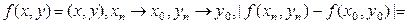


 ЧТД,
ЧТД,
Примеры Гильбертовых пр-в.
 1.
1.  Нер-во Шварца запис. в виде:
Нер-во Шварца запис. в виде:  - Нер-во Коши-Буняковского
- Нер-во Коши-Буняковского
2.  . Сх-ть ряда следует из оценки.
. Сх-ть ряда следует из оценки. 
3.  . Опред-е корректно в силу нер-ва Шварца, К-Б.
. Опред-е корректно в силу нер-ва Шварца, К-Б. 
Ортогональность.
Пусть Н-ГП. х н-ся ортогонально y 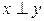 если
если  . Бесконечная система
. Бесконечная система 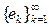 н-ся лин. независимой, если линейно-независима любая её конечная подсистема. Бесконечная сист.
н-ся лин. независимой, если линейно-независима любая её конечная подсистема. Бесконечная сист.  н-ся ортогональной, если
н-ся ортогональной, если  и ортонормированной, если
и ортонормированной, если 
Утверждение. Ортогональная система линейно независима. Д-во: 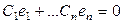 умножим скалярно на
умножим скалярно на 
 ЧТД,
ЧТД,
Теорема Пифагора. Если 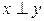 , то
, то  . Д-во:
. Д-во: 
 ЧТД.
ЧТД.
 Обобщенная теорема Пифагора. Если
Обобщенная теорема Пифагора. Если 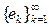 - ортогональн. система, то
- ортогональн. система, то  Д-во: самостоятельно.
Д-во: самостоятельно.
Р-во параллелограмма.  Д-во: самост-но ЧТД.
Д-во: самост-но ЧТД.
Замечание. Пусть  - пр-во измеримых суммируемых с квадратом с весом
- пр-во измеримых суммируемых с квадратом с весом  ф-ций, т.е.
ф-ций, т.е. 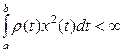 . Введем скал-е произвед-е:
. Введем скал-е произвед-е:  , вещ-е.
, вещ-е.
Если применять независ. системе процесс ортогонализации Шмита, то м. получить многие известные ортонормированные системы.
Теорема (процесс ортогонализации Шмитта). По люб. незав. системе 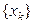 м. построить ортогональную систему
м. построить ортогональную систему  и ортонормир-ю систему
и ортонормир-ю систему  с помощью ф-л:
с помощью ф-л:  (без д-ва)
(без д-ва)
Расстояние от точки до мн-ва. 
Если  то
то  н-ся элементом наилучшего приближения элемента х элементами мн-ва M. В НП такой эл-т м.б. неединственным. В ГП эт-т наил. приближ-я опред-ся однозначно.
н-ся элементом наилучшего приближения элемента х элементами мн-ва M. В НП такой эл-т м.б. неединственным. В ГП эт-т наил. приближ-я опред-ся однозначно.
 9. Расст-е от т. до мн-ва. Т. о расстоянии. Проекция. Разложение ГП в прямую сумму.
9. Расст-е от т. до мн-ва. Т. о расстоянии. Проекция. Разложение ГП в прямую сумму.
Лемма. М – замкн. мн-во. Если  , то
, то  . Если
. Если 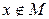 , то
, то  Д-во:
Д-во: 

 Пусть
Пусть 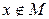 ПП
ПП  . По опр-ю инфинума
. По опр-ю инфинума  . Устремим
. Устремим  . Получим, что
. Получим, что  х – пред-я точка М, а т.к. М – замкнуто, то
х – пред-я точка М, а т.к. М – замкнуто, то  - это противоречие.
- это противоречие.
Теорема. Пусть М – замкнутое выпуклое мн-во в ГП Н и т. 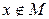 . Тогда
. Тогда  . Д-во: Обозначим
. Д-во: Обозначим  . По опр-ю инфинума
. По опр-ю инфинума  (1). Покажем, что посл-ть
(1). Покажем, что посл-ть  фундам-на. Запишем р-во параллелограмма со сторонами
фундам-на. Запишем р-во параллелограмма со сторонами  и
и  :
: 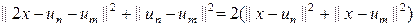



 Такое N сущ-т =>
Такое N сущ-т =>  - фундаментальна. Значит, т.к. ГП – полное, то
- фундаментальна. Значит, т.к. ГП – полное, то  т.к. М – замкнуто. Покажем, что этот эл-т единственный. ПП
т.к. М – замкнуто. Покажем, что этот эл-т единственный. ПП  Запишем р-во параллелограмма со стор.
Запишем р-во параллелограмма со стор.  :
: 


 Такой эл-т единственный. ЧТД.
Такой эл-т единственный. ЧТД.
 Замечание. Если мн-во М – незамкнутое, то такой эл-т может не существовать. Если М – невыпукло, то такой эл-т м.б. неединств.
Замечание. Если мн-во М – незамкнутое, то такой эл-т может не существовать. Если М – невыпукло, то такой эл-т м.б. неединств.
Пусть  -ГП и
-ГП и  . Ортогональной проекцией х на L н-ся элемент -
. Ортогональной проекцией х на L н-ся элемент - 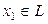 такой, что
такой, что 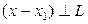
Расстояние от точки до подпр-ва. Пусть  , т.к. подпр-во L – замкн. выпуклое мн-во, то
, т.к. подпр-во L – замкн. выпуклое мн-во, то 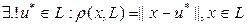
Теорема. Пусть 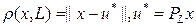 - проекция ортогональная х на подпр-во L. Д-во: Покажем, что
- проекция ортогональная х на подпр-во L. Д-во: Покажем, что  . И это будет означать, что
. И это будет означать, что 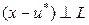 . Пусть
. Пусть  . Тогда
. Тогда  возв-м в квадрат
возв-м в квадрат  .
. 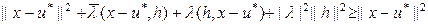 .
. 
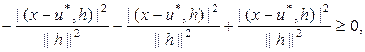
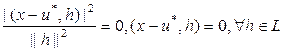 . Мы проверим, что
. Мы проверим, что  . ЧТД,
. ЧТД,
Утверждение. Пусть L натанут 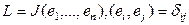 Тогда
Тогда  (2). Д-во:
(2). Д-во:  . Т.к.
. Т.к.  , то
, то  Значит
Значит 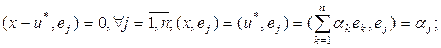

 ЧТД.
ЧТД.