МНК позволяет найти параметры «наилучшей» расчетной кривой, такой, чтобы ее расхождение с результатами опыта было минимальным. Отметим, что метод не дает вида зависимости y (x). Последний выбирается либо из теоретических представлений, либо по данным эксперимента. Поэтому перед использованием МНК нужно убедиться, что опытные данные действительно соответствуют предполагаемой зависимости. Для этого прежде всего необходимо построить график по результатам опыта.
Метод основан на том, что критерием «наилучших» параметров искомой зависимости является минимальность суммы S квадратов отклонений опытных точек  от расчетной кривой, т.е. минимум величины
от расчетной кривой, т.е. минимум величины
 ,
,
где  – значение искомой функции в i- й точке. Условия минимума при варьировании значений параметров
– значение искомой функции в i- й точке. Условия минимума при варьировании значений параметров  – равенство нулю соответствующих производных:
– равенство нулю соответствующих производных:  (индекс i = 1, 2,..., m) – дают m уравнений для отыскания m неизвестных параметров
(индекс i = 1, 2,..., m) – дают m уравнений для отыскания m неизвестных параметров  расчетной зависимости f (x).
расчетной зависимости f (x).
МНК наиболее прост для линейной зависимости y = Kx + b, которая содержит два неизвестных параметра: K и b. В этом случае сумма наименьших квадратов отклонений
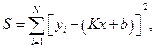
достигается при выполнении условий  и
и  , из которых получены для искомых параметров следующие уравнения:
, из которых получены для искомых параметров следующие уравнения:
 ; (8)
; (8)
 или
или  , (9)
, (9)
где суммы вычисляют по всем опытным точкам (N слагаемых).
Уравнение (9) показывает, что расчетная прямая проходит через следующие две точки: начальную (x =0; y = b) и среднюю ( ). При этом расположение опытных точек по отношению к прямой таково, что отклонения отдельных точек
). При этом расположение опытных точек по отношению к прямой таково, что отклонения отдельных точек  «выравниваются»: именно в этом случае сумма S минимальна. Если на графике есть одна точка с большим отклонением от прямой, то для выполнения условия
«выравниваются»: именно в этом случае сумма S минимальна. Если на графике есть одна точка с большим отклонением от прямой, то для выполнения условия 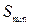 эта точка «подтянет» к себе расчетную прямую.
эта точка «подтянет» к себе расчетную прямую.
Для расчета среднего квадратического отклонения (СКО) искомых параметров (случайной погрешности) МНК дает следующие выражения:
 ;
; 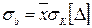 ,
,
где  ;
; 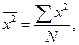
Расчеты по МНК обычно проводят на ЭВМ, используя стандартные программы. В лаборатории удобен программируемый микрокалькулятор, а также обычный микрокалькулятор с ячейкой памяти для вычисления сумм.
Пример применения МНК
При использовании метода выполняют следующие операции.
1 Из теории или опытных данных выясняют вид зависимости. Если она линейная (например, известно уравнение температурной зависимости сопротивления металлов  ) или же из графика видно, что опытные точки располагаются близко к некоторой прямой, то можно применять для расчета ее параметров формулы (8), (9). Если экспериментальная зависимость нелинейная, то стараются преобразовать ее в линейную (см. функциональные шкалы).
) или же из графика видно, что опытные точки располагаются близко к некоторой прямой, то можно применять для расчета ее параметров формулы (8), (9). Если экспериментальная зависимость нелинейная, то стараются преобразовать ее в линейную (см. функциональные шкалы).
2 Для расчетов параметров K и b по формулам (8), (9) предварительно вычисляют необходимые суммы по всем опытным точкам, а затем уже рассчитывают сами величины.
3 Наносят на поле графика начальную (x =0; y = b) и среднюю ( ) точки и проводят через эти точки расчетную прямую, чтобы убедиться, что отклонения от нее опытных точек действительно минимальны.
) точки и проводят через эти точки расчетную прямую, чтобы убедиться, что отклонения от нее опытных точек действительно минимальны.
4 Используя найденные значения параметров K и b, вычисляют случайные погрешности СКО этих величин по приведенным выше формулам. Записывают уравнение экспериментальной прямой и по найденным параметрам рассчитывают необходимые физические величины. Так, в примере с зависимостью R (t) находят температурный коэффициент сопротивления ( ), где величина
), где величина  .
.
ПРИЛОЖЕНИЕ
6.1 Вывод расчетной формулы для определения e/m методом магнетрона
Магнетрон – это прибор, состоящий из нити накала радиусом а и коаксиального цилиндрического анода радиусом b, которые находятся в однородном магнитном поле, параллельном нити. Между нитью и анодом приложена ускоряющая разность потенциалов U. Найти значение индукции магнитного поля, при котором электроны, вылетающие с нулевой начальной скоростью из нити, будут достигать анода.

Рисунок Магнетрон
На рисунке показаны силы, действующие на электрон, движущийся со скоростью v в произвольной точке траектории.
Сила Лоренца сообщает электрону нормальное ускорение  , в результате чего он движется по криволинейной траектории с радиусом кривизны R = mv / eB. По мере движения электрона от катода к аноду в электрическом поле скорость его растет, что ведет к увеличению R, т.е. траектория частицы не является окружностью.
, в результате чего он движется по криволинейной траектории с радиусом кривизны R = mv / eB. По мере движения электрона от катода к аноду в электрическом поле скорость его растет, что ведет к увеличению R, т.е. траектория частицы не является окружностью.
Интересующее нас значение магнитной индукции B, при котором траектория электрона касается поверхности анода, определяет силу Лоренца, входящую в уравнение динамики движения частицы. Запишем это уравнение для вращения электрона вокруг оси О магнетрона (относительно этой оси момент силы 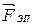 равен нулю). Изменение момента импульса электрона
равен нулю). Изменение момента импульса электрона

или
 , (1)
, (1)
где 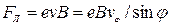 ;
; 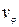 – составляющая скорости, перпендикулярная радиальной
– составляющая скорости, перпендикулярная радиальной  .
.
В уравнении (1) содержатся 4 переменные (vj, r, j, t), причем для первых двух очевидны граничные условия (см. рисунок): при изменении расстояния электрона от оси r от а до b составляющая его скорости vj изменяется от нуля до v (модуля скорости). Поэтому преобразуем уравнение (1), оставляя в нем переменные r и vj. После подстановки значения  в правую часть уравнения получим
в правую часть уравнения получим
 , (1а)
, (1а)
где tg j найдем из рис. 1. Сместив радиус r на угол dj, получим два треугольника (заштрихованы), из которых следует соотношение
 . (2)
. (2)
Чтобы исключить из уравнений переменные угол j и время t, запишем формулу для угловой скорости, связывающей эти величины:
 . (3)
. (3)
С учетом выражений (2) и (3) уравнение динамики приводится к виду
 . (4)
. (4)
Это уравнение в полных дифференциалах при начальных условиях r 0 = a, v 0 = 0 имеет следующее решение:
 . (5)
. (5)
Для точки касания поверхности анода расстояние от оси r = b и скорость электрона v j = v (см. рисунок), а значение скорости определяется разностью потенциалов в электрическом поле: mv 2/2= eU. Подстановка этих значений в уравнение (5) дает следующий ответ:
 . (6)
. (6)
Электроны, вылетевшие из катода с нулевой начальной скоростью, будут достигать поверхности анода при B << B кр.
В случае тонкой нити, принимая, что а << b, из уравнения (6) получаем формулу
 , (7)
, (7)
с которой совпадает расчетная формула, найденная в лабораторной работе № 6 в приближении постоянной скорости электрона v, приобретенной вблизи нити катода.
6.2 Таблицы:
Таблица 1 Удельные сопротивления и температурные коэффициенты сопротивления
| Элемент | Удельное сопротивление r, нОм×м (при 20 °С) | Температурный коэффициент

|
| Алюминий Вольфрам Медь Свинец Серебро Нихром | 25,3 55,0 17,1 190,0 15,0 1100,0 | 4,5 5,1 4,3 4,2 4,1 0,2 |
Таблица 2. Постоянная Холла и ширина запрещенной зоны
| Элемент | Ширина запрещенной зоны D W, эВ (при 20 °С) | Постоянная Холла, 10–10 м3/Кл (при 20 °С) |
| Магний | 0,69 | –0,9 |
| Алюминий | 1,32 | –0,379 |
| Германий | 0,63 | +109 |
| Олово | 1,55 | –0,048 |
| Теллур | 0,35 | +0,24 |