ОПРЕДЕЛЕНИЕ
Всякое рефлексивное, симметричное и транзитивное отношение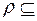 
А 
А, называется отношением эквивалентности.
Если r - отношение эквивалентности и a r b, то элементы a и b называются эквивалентными в этом отношении или просто эквивалентными.
Рассмотренное ранее отношение " быть родственником " является отношением эквивалентности. Аналогично, отношением эквивалентности на множестве всех людей является отношение " быть однофамильцем ". Это отношение связывает между собой людей с одинаковыми фамилиями, распределяя их по классам людей, каждый из которых состоит из всех людей, имеющих одну и ту же фамилию.
Для представления фундаментального свойства отношений эквивалентности введем понятие разбиения множества.
ОПРЕДЕЛЕНИЕ
Разбиением множества A называется конечное или бесконечное семейство множеств Ai, i Î I таких, что:
1) " i ÎI(Ai ¹ 
);
2) " i,jÎI(i 
j Þ Ai Ç Aj = );
3) 
Ai = A.
Здесь I это множество значений нижнего индекса множеств разбиения. В разбиениях счетных множеств в качестве множества индексов I обычно применяется все или часть множества натуральных чисел.
Пусть A 1,..., A k,... - разбиение множества A. Нетрудно проверить, что отношение r на множестве A, определяемое соотношением: a r b 
, является отношением эквивалентности.
Следующая теорема показывает, что справедливо и обратное свойство.
ТЕОРЕМА 3.2
Всякое отношение эквивалентности на множестве A разбивает это множество на классы эквивалентных элементов.
Доказательство
Разобьем доказательство теоремы на несколько этапов.
1. Построение разбиения, порождаемого отношением r.
Пусть r - отношение эквивалентности на множестве A.
Для каждого x 
A обозначим как [ x ] множество { y ½ x r y }. Поскольку отношение r рефлексивно, то x Î [ x ], а, значит, каждое множество [ x ] является непустым и система множеств [ x ], где x Î A, содержит все элементы A. Из семейства множеств {[ x ]| x Î A } удалим кратные вхождения одинаковых множеств. В результате получим семейство непустых несовпадающих множеств R, в которых содержатся все элементы A.
2. Обоснование того, что R образует разбиение.
Пусть [ x ] и [ y ] - произвольные классы из семейства R. Покажем, что они либо не пересекаются, либо совпадают, т.е. возможны только два случая:
1) [ x ] Ç [ y ] = ;
2) [ x ] Ç [ y ] .
Предположим, что это свойство является неверным. То есть для некоторых двух элементов x и y множества [ x ] и [ y ] пересекаются, но не совпадают (рис 3.1).
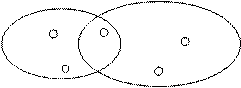[ x ] [ y ]
x z y
ab
Рис. 3.1
Здесь z - это элемент, общий для классов [ x ] и [ y ], а a и b - произвольные элементы в [ x ] и [ y ] соответственно.
1. Докажем, что [ x ] 
[ y ]. Пусть x r a. Покажем, что
справедливо отношение y r a:
a) поскольку x r z, то из симметричности r следует, что
z r x;
b) поскольку z r x и x r a, то из транзитивности r вытекает, что z r a;
c) из y r z и z r a и транзитивности r имеем y r a. Поэтому aÎ [ y ], а, значит, [ x ] [ y ].
2. Обратное включение [ y ] [ x ] может быть доказано, если повторить проведенные рассуждения, поменяв в них местами x и y, а также a и b.
Следовательно, справедливо равенство множеств [ x ] и [ y ]. Последнее противоречит предположению о том, что эти множества являются разными.
Это означает, система множеств R образует разбиение множества разбиение A.
3. Обоснование того, что R разбивает A на классы эквивалентных элементов.
3.1. Покажем, что в каждом классе из R любые два элемента находятся между собой в отношении r.
Пусть выбраны произвольное множество [ x ] Î R и элементы a, b Î A. Покажем, что a r b. Действительно, по определению множества [ x ] справедливы соотношения: x r a и x r b. Из соотношения x r a и симметричности r следует, что a r x. Из a r x и x r b, а также транзитивности r следует, что a r b.
3.2. Покажем, что элементы из разных классов в R не находятся в отношении r. Пусть [ x ], [ y ] Î R и a Î[ x ], b Î[ y ] - произвольные элементы этих множеств. Покажем, что (a, b) Ï r. Предположим противное. Пусть a r b. Тогда из симметричности отношения r следует, что b r a. Поскольку y r b и b r a, то из транзитивности r следует, что y r a. Поэтому a Î[ y ]. Последнее противоречит тому, что множества [ x ] и [ y ] не пересекаются.
Следовательно, (a, b) Ï r.