1) вероятность суммы двух событий А и В можно найти по формуле:
 , (9)
, (9)
если события несовместны, то
 ; (4)
; (4)
2) вероятность суммы n событий:
 (11)
(11)
Терема умножения вероятностей
1) вероятность произведения двух событий
 ; (12)
; (12)
если события А и В независимы, то
 ; (5)
; (5)
2) вероятность произведения n событий
 ;
;
если события  независимы в совокупности (т.е. каждое событие из совокупности попарно независимо с остальными, а также со всевозможными произведениями остальных событий), то
независимы в совокупности (т.е. каждое событие из совокупности попарно независимо с остальными, а также со всевозможными произведениями остальных событий), то  .
.
Формула полной вероятности
Пусть задана полная группа событий: { H 1, H 2, …, Hn }. Для них выполняется:  . Тогда вероятность некоторого события А, зависимого от H 1, H 2, …, Hn можно найти по формуле:
. Тогда вероятность некоторого события А, зависимого от H 1, H 2, …, Hn можно найти по формуле:
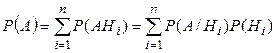 . (6)
. (6)
Формула Байеса
1) для событий А и В:
 ;
;
2) для полной группы событий (гипотез) вероятность гипотезы при условии, что событие А произошло, равна:
 . (7)
. (7)
Формула Бернулли
Пусть при проведении серии n независимых испытаний в каждом из них событие А происходит с вероятностью р и не происходит с вероятностью  . Пусть при этом событие В заключается в том, что событие А в серии n независимых испытаний произошло m раз. Тогда вероятность события В можно найти по формуле:
. Пусть при этом событие В заключается в том, что событие А в серии n независимых испытаний произошло m раз. Тогда вероятность события В можно найти по формуле:
 . (8)
. (8)
Локальная формула Муавра-Лапласа (предельная теорема Муавра-Лапласа):
 . (17)
. (17)
Формула даёт наиболее точное значение при n > 100, а npq > 20.
Исходя из формулы Муавра-Лапласа, вероятность события В (в серии n независимых испытаний событие А произошло m раз) можно также получить, используя функцию Гаусса (её значения приведены в приложении Б):  , тогда
, тогда
 . (9)
. (9)
Интегральная формула Муавра-Лапласа
При большом числе испытаний в качестве события В рассматривают событие, заключающееся в том, что число успехов (наступлений события А) лежит в некотором интервале. Тогда справедлива интегральная предельная теорема Муавра-Лапласа:
 (19)
(19)

Так как значения функции  (функции Лапласа) известны (приложение Б), то вероятность события В, исходя из интегральной формулы Муавра-Лапласа, находят следующим образом:
(функции Лапласа) известны (приложение Б), то вероятность события В, исходя из интегральной формулы Муавра-Лапласа, находят следующим образом:
 (10)
(10)
Формула Пуассона
Нахождение вероятности события B (в серии n независимых испытаний событие А произошло m раз) по формуле Бернулли при больших  затруднителен. Но в случае малой вероятности
затруднителен. Но в случае малой вероятности  успеха, можно оценить вероятность B следующим образом: если
успеха, можно оценить вероятность B следующим образом: если  и
и  , то
, то  . Обозначив
. Обозначив  , получим:
, получим:
 . (11)
. (11)
Параметр  равен среднему числу успехов в серии из
равен среднему числу успехов в серии из  испытаний, т.е. ожидаемому числу успехов, где под
испытаний, т.е. ожидаемому числу успехов, где под  понимается частота успеха.
понимается частота успеха.
Случайные величины
Случайная величина – переменная величина, которая принимает значения в зависимости от исходов испытания, т.е. случайным образом. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены, [1, с. 57].
Дискретная случайная величина – случайная величина, принимающая конечное или счётное множество значений.
Непрерывная случайная величина – случайная величина, принимающая значения из некоторого промежутка.
Закон распределения дискретной случайной величины – соответствие между значениями  этой величины и их вероятностями
этой величины и их вероятностями  . Закон распределения дискретной случайной величины задаётся таблично или аналитически:
. Закон распределения дискретной случайной величины задаётся таблично или аналитически:
1) табличное задание (табл.1)
Таблица 1 – Закон распределения дискретной случайной величины Х
| Х | 
| 
| 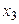
| 
| 
|
| Р | 
| 
| 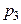
| 
| 
|
2) аналитическое:
 , при этом
, при этом  , [3, c. 52].
, [3, c. 52].