Типовые регуляторы в цифровой реализации

Глава II

Законы и алгоритмы цифрового регулирования

Обзор законов локального цифрового управления

Исполнительными устройствами роботов

Как было показано основными исполнительными устройствами в роботах являются электроприводы, поэтому наиболее сложными проблемами заключаются в разработке прямого цифрового управления электроприводами. Для станков с ЧПУ и для промышленных роботов в настоящее время применяются в основном локальные регуляторы, построенные по принципу подчиненного (каскадного) регулирования. Широкое применение таких регуляторов обусловлено простотой расче­та отдельных контуров, последовательным решением задач ограниче­ния координат, облегчением процесса отладки, унификация отдельных узлов управления. Именно развитие аналоговой техники и особен­но появление интегральных операционных усилителей способствовало быстрому внедрению систем управления электроприводами с подчинен­ным регулированием.

При прямом цифровом управлении на базе микропроцессорной тех­ники законы регулирования реализуются в виде цифровых алгоритмов. Это позволяет повысить точность управления, обеспечить стабильность параметров настраиваемых контуров, упростить средства сопряжения локальных регуляторов с цифровой системой управления верхнего уров­ня, улучшить эксплуатационные характеристики, например, за счет ав­томатического самоконтроля и контроля ЭВМ верхнего уровня за рабо­той регуляторов.

При создании цифровых регуляторов в основном копировались за­коны управления, разработанные для аналоговых. Это создает преемственность, возможность использования опыта анализа, синтеза и настройки аналоговых регуляторов при разработке цифровых. Однако, цифровые алгоритмы при такой прямом копировании не улучшили дина­мику электроприводов. Это связано с тем, что цифровые регуляторы из-за квантования по времени имеют худшие динамические характерис­тики, чем непрерывные (аналоговые) регуляторы, реализующие те же самые законы управления» В то же время цифровые системы имеют значительно большие потенциальные возможности для реализации слож­ных законов управления (оптимальных, адаптивных и т.д.), которые позволяют получить статические и динамические характеристики в сис­темах управления, практически недостижимые при использовании ана­логовых регуляторов.

Применение микропроцессорных (цифровых) систем управления предоставляет разработчику более широкие возможности в выборе ти­пов регуляторов. Технически цифровые регуляторы будут одинаковыми. Отличие заключается лишь в программах управления. Т.е. сложность законов управления не влечет за собой усложнение технической реа­лизации.

По способу синтеза цифровые регуляторы можно разделить на две основные группы: параметрически оптимизируемые и структур­но оптимизируемые. В параметрически оптимизируемых регуляторах структура (программа управления) задана, и задача синтеза сводит­ся к определению параметров (коэффициентов), при которых обеспечи­вается заданное качество управления. К таким регуляторам относят­ся типовые регуляторы: И, ПИ, ПИД.

В структурно оптимизируемых регуляторах структура и парамет­ры являются изменяемыми в зависимости от вида объекта и требований к качеству управления. Такие регуляторы можно условно разделить на три группы: компенсационные, апериодические с конечным временем установления и регуляторы состояния. Выбор типа регуляторов зави­сит от требований к статическим и динамическим характеристикам процесса управления и от технический возможностей микропроцессор­ной системы, с помощью которой реализуется регулятор.

 

Типовые регуляторы в цифровой реализации

К типовым регуляторам относятся пропорциональные (П), интег­ральные (И), пропорционально-интегральные (ПИ) и пропорционально-интегрально-дифференциальные (ПИД) регуляторы. Цифровой И-регулятор был рассмотрен в качестве примера в § 1.1. Этот регулятор является частным случаем ПИД-регулятора. Уравнение непрерывного ПИД-регулятора имеет вид

 

(2.1)

 

Или применяя преобразование Лапласа, получим

 

(2.2)

 

Такой регулятор наиболее часто применяется на практике. В частнос­ти, система подчиненного регулирования состоит из каскадно вклю­ченных ПИ- и П-регуляторов. Интегральная составляющая обеспечива­ет точность в установившемся режиме, П и Д - составлявшие служат для получения требуемых динамических показателей (длительности пе­реходного процесса, колебательности, величины максимального перерегулирования).

При малых значениях периода Т уравнение (2.1) можно предста­вить в виде разностного

 

(2.3)

 

Выражение (2.3) представляет не рекуррентный алгоритм управления. Как было ранее показано, для цифрового управления удобнее реализовать рекуррентный алгоритм. Для его определения найдем

 

 

Вычитая это уравнение из уравнения (2.3) получим

 

, (2.4)

где ; ;

 

Выражение (2.4) справедливо при малых значениях периода кван­тования. Для больших периодов квантования необходимо использовать точную дискретную модель. Как было доказано в главе I, ее наиболее просто получить с помощью Z - или D - преобразований. В этом случае алгоритм управления записывается относительно идеальных импульсных сигналов (рис.1.2 б), а реальная форма импульсных сигна­лов с выхода управляющей ЭВМ учитывается формирующим элементом.

Согласно (2.4) Z-преобразованное выражение для дискретно­го ПИД-регулятора будет иметь вид

 

(2.5)

 

Подчеркнем еще раз, что отличие от (2.4) состоит в том, что коэф­фициенты q₀, q₁, q₂ не зависят от длительности импульсов, т.к. они учитываются в формирующем звене, объединяемом при получении диск­ретной передаточной функции с объектом управления (см. (1.20)).

Согласно (2.5) дискретная передаточная функция регулятора

 

(2.6)

Наличие полюса Z=1 говорит о том, что в установившемся режиме ошибка e(z) будет равна нулю (астатический регулятор)).

В общем случае передаточная функция астатического дискретного регулятора имеет следующий вид

 

(2.7)

 

По аналогии с выражением для непрерывного регулятора (2.2) уравнение дискретного регулятора (2.6) можно представить в следующем виде

 

(2.8)

 

Приравнивая в (2.6) и (2.8) коэффициенты при одинаковых степенях, получим

; ; . (2.9)

 

Если сравнивать эти коэффициенты с коэффициентами непрерывного ПИД-регулятора, то получим необычный вывод, что пропорциональная составляющего дискретного регулятора имеет отрицательный коэффициент. Это объясняется тем, что передаточная функция (2.6) соответствует рекуррентному алгоритму (2.4), и отрицательный коэффициент служит для "забывания" пропорциональной составляющей предыдущего такта. Т.е. пропорциональная составляющая определяется как первая разность интегральной составляющей.

Для получения большего сходства с непрерывным регулятором уравнение дискретного регулятора (2.2) можно представить в следующем виде

 

(2.10)

 

Выражение (2.10) отличается от (2.3) задержкой на один такт интегральной составляющей, что не принципиально. Уравнение (2.10) дает такой же вид рекуррентного алгоритма (2.5), что и представление (2.2), но взаимосвязь между коэффициентами будет другая

 

; ; . (2.11)

При таком алгоритме дискретный И-регулятор получается из (2.6) при n=1, q₀=0.

Уравнение (2.1) и (2.2) показывает, что в случае малых значений периода квантования Т связь между коэффициентами непрерывного и дискретного ПИД-регуляторов определяется следующими соотношениями

 

; ; . (2.12)

 

Определение коэффициентов дискретных регуляторов осуществляется теми же способами, что и для непрерывных систем: методом параметрической настройки, когда определяются критические значения коэффициентов, а затем они изменяются для получения заданного запаса устойчивости, либо путем расчета оптимальных коэффициентов, минимизирующих заданный критерий качества регулирования, например, квадратичный интегральный.

Рассмотрим способ определения критических коэффициентов дискретного регулятора. В §1.1 определено, что апериодическому звену первого порядка (1.11) соответствует дискретная передаточная функция

 

.

 

В результате обратного Z преобразования получим следующее разностное уравнение

 

.

 

Уравнение свободного движения определяется при u(k)=0

 

.

 

Найдем y_св(k) при k=1,2,3,…

 

; ; … .

 

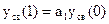При этом следует, что свободное движение будет стремится к 0 (что является признаком устойчивости объекта), если a₁<1. Таким же образом можно доказать, что объект или замкнутая система регулирования n - порядка будут устойчивы, если корни характеристического уравнения их дискретных передаточных функций (1.23) будут меньше единицы. Это означает, что на комплексной плоскости все корни характеристического уравнения должны лежать внутри единичной окружности.

Для непрерывной системы условие устойчивости сводится к необходимости нахождения корней характеристического уравнения в левой плоскости. Поэтому, чтобы использовать критерии устойчивости, разработанные для непрерывных систем, для исследования дискретных передаточных функций осуществляют замену переменной Z на w, которые связаны следующей зависимостью

. (2.13)

Такая замена переводит внутренность единичного круга Z - плоскости в левую полуплоскость w. Следовательно, для дискретных передаточных функций относительно переменной w можно применять критерии устойчивости, разработанные для линейных систем.

Рассмотрим определение критического коэффициента дискретного И-регулятора для объекта первого порядка (см. §1.1). Согласно выражению (1.33) характеристическое уравнение замкнутой системы имеет вид

 

.

 

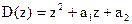Приведя к общему знаменателю и взяв числитель, получим

 

.

 

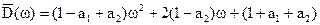Согласно критерия Гурвица в устойчивой системе второго порядка все коэффициенты должны быть положительны

 

; ; .

 

Подставив в первое неравенство выражение для коэффициентов из (1.25) и (1.33) получим

 

Следовательно, критический коэффициент дискретного И-регулятора k_И^* определяется выражением

 

.

 

Для получения качественных переходных процессов величину нужно уменьшить в 2¸3 раза.

Аналогично находят критические коэффициенты дискретных регуляторов более высоко порядка.

Для расчета оптимальных типовых регуляторов разработаны рекомендации и стандартные соотношения. Поэтому подробно на этом вопросе останавливаться не будем.

Другим важным вопросом является выбор периода квантования Т. Максимальное его значение определяется исходя из теоремы Котельникова-Шеннена. Для того, чтобы непрерывный сигнал со спектром, ограниченный максимальной частотой w_max, можно было восстановить по его дискретной последовательности, необходимо соблюдение условия

 

 

где w_Т=2p/Т - круговая частота квантования.

На основании этого условия период квантования должен быть меньше минимальной величины из следующего набора

 

(2.14)

 

где w_f - максимальная частота возмущающего воздействия;

w_з - максимальная частота задающего сигнала;

w_е - максимальная колебательная составляющая свободного движения объекта;

t_п - минимальное время переходного процесса;

n - порядок системы уравнения.

При заданном значений Т выражение (2.14) определяет максимальное значение частот, которые дискретная замкнутая система будет отрабатывать. При неизвестных значения спектра внешних сигналов выбор периода Т на начальном этапе проектирования можно определить из условия

 

; (2.15)

 

где Т_Omin - минимальная постоянная времени непрерывной передаточной функции объекта.

Условие при котором поведение дискретной замкнутой системы приближается к непрерывной приближенно можно определить следующим неравенством

 

. (2.16)

 

Очевидно, что при соблюдении соотношения (2.16) расчет коэффициентов ПИД-регулятора можно производить по рекомендациям, разработанных для непрерывных систем управления. При переходе к дискретному алгоритму ПИД-регулятора, его коэффициенты пересчитываются в соответствии с зависимостями (2.12).

Структурная схема регулятора, соответствующая алгоритму уравнения (2.4) или (2.8) представлена на рис.2.1 а. С целью ограничения начального броска управляющего воздействия с выхода регулятора при резком изменении задающего сигнала u_з(к), чаще применяют модифицированный алгоритм, структурная схема которого представлена на рис. 2.1 б. В этом регуляторе пропорциональная и дифференциальная составляющие берутся не от ошибки регулирования, а от выходной координаты

 

.

 

При резком изменении u_з(к) интегральная составляющая сигнала с выхода регулятора будет нарастать постепенно, а скорость изменения пропорциональной и дифференциальной составляющей ограничиваются из-за инерционности объекта.

Очевидно, что программная реализация рассмотренных регуляторов достаточно проста.