Глава 7
Собственные интегралы (Римана), зависящие от параметра
Пусть f(x,y) – функция двух переменных, определённая на прямоугольнике
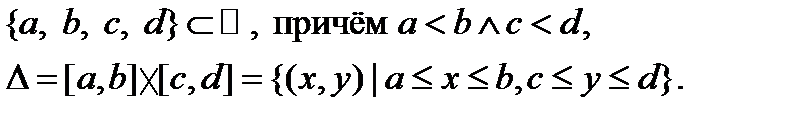


 Если для любого существует интеграл, то этот интеграл является функцией от переменной y (которая и называется здесь параметром):
Если для любого существует интеграл, то этот интеграл является функцией от переменной y (которая и называется здесь параметром):
Таким образом, мы получаем новый способ задания функции – в виде интеграла, зависящего от параметра, т.е. определяемые т.о. функции часто используют в математических рассуждениях и приложениях.
Следует иметь ввиду, что

 Пример 1. Рассмотрим функцию
Пример 1. Рассмотрим функцию
В этом примере интеграл легко вычислить:



Значит, можно задать и обычным способом:
Однако часто встречаются интегралы, которые не выражаются через элементарные функции. Тогда приходится работать с функцией, заданной в виде интеграла с параметром. Значит, нужно научиться работать с такими функциями – в частности, знать правила их дифференцирования и интегрирования.
Возможна и более сложная ситуация, когда от параметра зависит не только подынтегральная функция, но и пределы интегрирования:

Основные теоремы
Предельный переход под знаком интеграла
 Теорема 1 ( о непрерывности интеграла с параметром ).
Теорема 1 ( о непрерывности интеграла с параметром ).

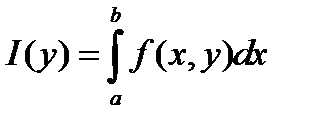 Если функция f(x,y) непрерывна на прямоугольнике то
Если функция f(x,y) непрерывна на прямоугольнике то
функция непрерывна на отрезке
 Доказательство. По теореме Кантора, непрерывная на компактном множестве ∆ функция является равномерно непрерывной, т.е.
Доказательство. По теореме Кантора, непрерывная на компактном множестве ∆ функция является равномерно непрерывной, т.е.


 Возьмём Тогда из равномерной непрерывности следует:
Возьмём Тогда из равномерной непрерывности следует:
Оценим теперь приращение функции I (y):

Итак, что и означает непрерывность функции I (y).
Замечание. В теореме 1 требуется, чтобы f (x,y) была непрерывной по обеим переменным в совокупности, т.е. чтобы

 Недостаточно, чтобы f (x,y) была непрерывной по каждой из переменных. Например, функция
Недостаточно, чтобы f (x,y) была непрерывной по каждой из переменных. Например, функция
 непрерывна по x (при любом фиксированном y), и непрерывна по y (при любом фиксированном x). Однако она не является непрерывной в точке (0,0) функцией (по совокупности переменных): предел не
непрерывна по x (при любом фиксированном y), и непрерывна по y (при любом фиксированном x). Однако она не является непрерывной в точке (0,0) функцией (по совокупности переменных): предел не
 существует. В данном случае не справедлив и вывод теоремы 1; например, функция
существует. В данном случае не справедлив и вывод теоремы 1; например, функция
разрывна в точке y = 0.
 Так как непрерывность в точке I (y) означает, по определению, что
Так как непрерывность в точке I (y) означает, по определению, что
в любой точке y 0, то непосредственно из теоремы 1
вытекает

 Теорема 2 ( о предельном переходе под знаком интеграла ).
Теорема 2 ( о предельном переходе под знаком интеграла ).
Если f (x,y) непрерывна на то для любого
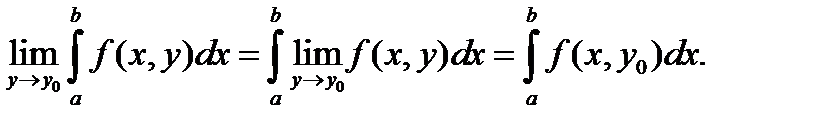
 Если – непрерывные функции, а f (x, y) непрерывна на множестве
Если – непрерывные функции, а f (x, y) непрерывна на множестве

 то можно доказать, что
то можно доказать, что
Это утверждение усиливает теоремы 1 и 2.
Ещё одно усиление теорем 1,2 связано с заменой требования непрерывности f (x, y) более слабым условием.
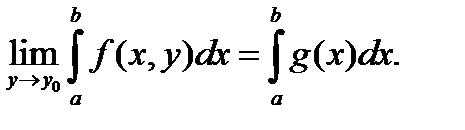 Теорема 3. Если f (x, y) непрерывна по x (при любом фиксированном y) и f (x, y) равномерно сходится к функции g (x) при y → y 0, то
Теорема 3. Если f (x, y) непрерывна по x (при любом фиксированном y) и f (x, y) равномерно сходится к функции g (x) при y → y 0, то
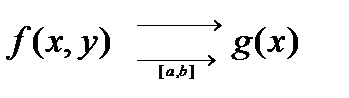
Равномерная сходимость: означает:

Доказательство. просто – оно проводится с помощью той же оценки, что и доказательство теоремы 1.
Теорема 3 справедлива также в случае y → ∞, лишь определение равномерной сходимости имеет другой вид:
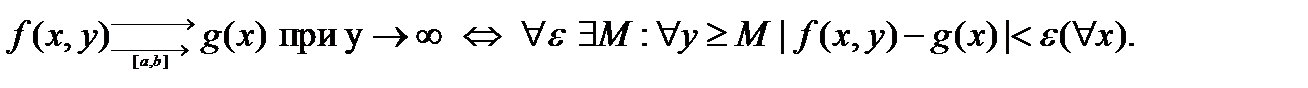
 Пример 2. Вычислить.
Пример 2. Вычислить.

Решение. Так как функция непрерывны при любых
x, y, то возможен предельный переход под знаком интеграла:


Пример 3. Вычислить.
 Решение. Подынтегральная функция непрерывна при любых x, y и y →∞ стремится к g (x)= x:
Решение. Подынтегральная функция непрерывна при любых x, y и y →∞ стремится к g (x)= x:

Эта система равномерная, так как

,

если только. Значит, возможен переход к пределу под
знаком интеграла:

.