Узкополосные случайные процессы

Случайный процесс (t) является узкополосным, если его плотность отлична от нуля только вблизи частоты f ₀. Для этих процессов выполняется условие

(3.27)

где f ширина спектральной плотности, определённая, например, на уровне 0.5 или каким-либо другим удобным способом, в том числе определённая как эффективная ширина.

Реализации узкополосного процесса имеют вид промодулиро­ванных по амплитуде и фазе гармонических колебаний. Поэтому узко­полосный случайный процесс может быть записан в виде

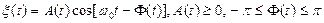, (3.28)

где A (t) и Ф (t) - медленно меняющиеся по сравнению с слу­чайные функции времени. В дальнейшем будем называть A (t) огибающей, a Ф(t) - фазой узкополосного случайного процесса.

Рассматривая A (t), Ф (t) как стационарные случайные процессы, поставим задачу найти их плотности вероятности р (а), р (), если узкополосный случайный процесс (t) является гауссовским случайным процессом с нулевым математи­ческим ожиданием = 0 и дисперсией = ².

Для решения поставленной задачи удобно, используя формулу , где , , представить в виде суммы квадратурных составляющих:

(3.29)

где - косинусная, a - синусная квадратурные составляющие случайного процесса. В свою очередь, огибающая и фаза будут равны:

(3.30)

(3.31)

Представление узкополосного случайного процесса через оги­бающую и фазу используется в полярной системе координат, а пред­ставление его через ортогональные составляющие и - в прямоугольной системе координат.

Если A _с(t), A _s(t) являются случайными процессами с гауссовским распределением, то, рассматривая и как детерми­нированные множители, приходим к выводу, что в любой момент вре­мени (t) как сумма гауссовских случайных величин имеет гауссовское распределение. Верно и наоборот, если (t) имеет гауссовское распределение с нулевым математическим ожиданием, то A _c (t) и A _s(t) являются также гауссовскими процессами с нулевым математическим ожиданием. Более того, если спектральная плотность случайного процесса (t) симметрична относительно f₀ и её корреляционная функция равна

то корреляционные функции процессов А_c(), А_s() совпадают между собой и определяются выражением

(3.32)

а их взаимная корреляционная функция равна нулю:

(3.33)

при любом .

Формулы (3.30), (3.31) позволяют интерпретировать A (t) как длину случайного вектора, случайные проекции которого на оси пря­моугольных координат равны A _c(t) и A _s(t), а фаза Ф (t) является углом между A (t) и осью абсцисс (рис. 3.3).

Рис. 3.3

Длина вектора A (t) и величина угла Ф (t) изменяются во време­ни случайным образом, так что конец вектора совершает случайные блуждания по плоскости. Однако в фиксированный момент времени t вектор неподвижен, так что можно рассматривать как случайные величины. В этом случае при известной двумерной плотности вероятности квадратурных составляющих р (а _с, а _s), где а _с, а _s - возможные значения A _c(f), A _s(t) в конкретный момент времени, зная функциональную связь (3.30), (3.31), можно определить двумерную плотность вероятности р (а, ),где а, - воз­можные значения A (t), Ф (t) в этот же момент времени. Затем, инте­грируя р (а, ) по возможным значениям , можно определить р (а), а путем интегрирования по а - р (). При этом плотность вероятности длины вектора (в нашем случае огибающей) р (а) имеет рэлеевское распределение, а аргумент (в нашем случае фаза) имеет равномерное распределение с плотностью вероятности р () = 1/2 . Графики р(а), р() приведены на рис. 3.4, а формулы для р (а) и р () соответственно равны:

Рис. 3.4

(3.34)

(3.35)