Численные методы поиска экстремумов функций одной переменной

Численные методы решения экстремальных задач

Пусть -функция, определенная на некотором множестве . Будем рассматривать задачу минимизации функции . Любая задача максимизации функции на равносильна задаче минимизации функции на том же множестве .

Классический подход.

Пусть непрерывная и гладкая функция на отрезке [a, b]. Тогда точками экстремума функции на [a, b] могут быть лишь те точки, в которых выполняются условия: производная существует и равна нулю; или . Такие точки принято называть точками подозрительными на экстремум. Поиск точек экстремума функции начинают с нахождения всех точек, подозрительных на экстремум. После того, как такие точки найдены, проводят дополнительное исследование и отбирают среди них те, которые являются точками локального минимума (максимума).

Чтобы найти глобальный минимум (максимум) функции на [a, b], нужно перебрать все точки локального минимума (максимума) на [a, b] и среди них выбрать точку с наименьшим (наибольшим) значением функции, если таковая существует (если вместо [a, b] имеем дело с R, то следует изучить поведение функции при или ).

К сожалению, классический метод имеет весьма ограниченное применение. В практических задачах вычисление зачастую является непростым делом. Например, значения функции определяется из наблюдений или эксперимента, и получить информацию о её производной крайне трудно. Поэтому важно иметь методы поиска экстремума, не требующие вычисления производной, удобные для реализации на ЭВМ.

Численные методы поиска экстремумов функций одной переменной

Задача поиска экстремумов сводится к их локализации и уточнению значений и в точке экстремума. Все численные методы предполагают, что локализация экстремумов каким-либо образом произведена (например, графически или аналитически) и задача численных методов будет состоять в уточнении полученных результатов с заданной точностью e. В дальнейшем для функций одной переменной под экстремумом будем подразумевать минимум . Будем считать, что Î[a,b], где a и b границы интервала поиска. В пределах отрезка [a,b] функция необязательно непрерывная, могут существовать разрывы первого рода. Достаточно чтобы функция на отрезке [a, b] была унимодальной, то есть, содержащей на указанном отрезке ОДИН минимум.

Метод равномерного поиска.

Этот метод основан на том, что переменной присваиваются значения c шагом h =const (шагом поиска), где i=0,1,2,… и вычисляются значения в соседних точкаx. Если , то переменной дается новое приращение. Как только становится , поиск останавливается и предпоследняя точка считается ответом.

Выбор (начального значения переменной ) определяется пользователем. Шаг поиска - фактическая погрешность определения результата. При поиске решения на отрезке, обычно в качестве начального приближения берут один из его концов, а при изменении переменной х предусматривается проверка на выход ее за границу отрезка.

Метод поразрядного приближения

является разновидностью метода равномерного поиска и реализуется следующим образом:

1. Задаем начальное приближение слева от минимума функции и вычисляем , задаем начальный шаг поиска h (выбирается вычислителем), точность e определения результата поиска (для переменной ), берем i=0.

2. Задаем и вычисляем .

3. Проверяем условие , если оно выполняется, то идем к пункту 2, увеличивая на 1.

4. Проверяем условие |h| ³ e. Если оно выполняется, полагаем h = -h/10, увеличиваем на 1 и идем к пункту 2, т.е. обеспечиваем поиск минимума в другом направлении с шагом h/10.

5. Выводим на печать полученное значение для переменной и функции .

Метод деления отрезка пополам (или метод дихотомии).

Поиск минимума на отрезке [a, b] на каждом шаге начинается с выбора двух точек и , где >0-постоянная, являющаяся параметром метода. Величина выбирается вычислителем и может определяться целесообразным количеством верных десятичных знаков при задании аргумента . Точки и расположены симметрично на [a, b] относительно его середины и при малых делят его почти пополам. Уточняем положение экстремума с заданной точностью .

Метод реализуется следующим алгоритмом:

1. Проверяем условие |b-a|<e. Если условие выполняется, идем к пункту 6.

2. Делим интервал поиска [a, b] точками и .

3. Для значений и вычисляем и .

4. Проверяем условие . Если оно выполняется, полагаем и идем к пункту 1.

5. Полагаем и идем к пункту 1.

6. Выводим на печать и .

Практическое задание:

Задать интервал, на котором функция имеет минимальное или максимальное значение; определить координаты точки минимума (максимума) и вычислить значение функции в этой точке_, с использованием различных методов.

№	F(x)
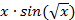