Задание 9.1. Решить задачу: В лотерее разыгрывается 100 билетов. Выигрыши выпали на 25 билетов. Некто приобрел 6 билетов. Найти вероятность того, что выигрыш выпадет на 2 билета.
Решение.
Пусть событие A - выигрыш выпал на 2 билета из 6. Тогда вероятность того, что выигрыш выпал на 2 из 6 билетов будет определяться по формуле:
P (A) =  .
.
Число всех возможных исходов n найдем по формуле n= C  =
=  = =
= =  = 4768209600. Число исходов m, благо-приятствующих появлению события A, найдем по формуле
= 4768209600. Число исходов m, благо-приятствующих появлению события A, найдем по формуле
m = C  ·C
·C  =
=  =
=  = 300·1215450 =
= 300·1215450 =
= 364635000. Тогда P (A) = 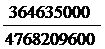
 0, 0765.
0, 0765.
Задание 9.2. Решить задачу:
а) Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.
б) Имеется пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит цель при выстреле из винтовки с оптическим прицелом, равна 0,95, для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что цель будет поражена, если стрелок произведет один выстрел из наугад выбранной винтовки.
в) Трое охотников одновременно выстрелили по медведю, который был убит одной пулей. Определить вероятность того, что медведь был убит первым стрелком, если вероятности попадания для этих стрелков равны соответственно 0,3; 0,4; 0,5.
Решение.
а) Обозначим попадание в цель первым стрелком – событие А, вторым – событие В, промах первого стрелка – событие 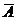 , промах второго – событие
, промах второго – событие  . Тогда в соответствии с условием задачи:
. Тогда в соответствии с условием задачи:
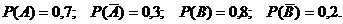
Обозначим за событие C то, что при одном залпе в мишень попадет только один из стрелков.Так как C =  , то
, то
P (C) = P ( ) = P (
) = P ( ) + P (
) + P ( ) =
) =  +
+ 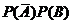 = 0,7·0,2 + + 0,3·0,8 = 0,14 + 0,24 = 0,38 (События
= 0,7·0,2 + + 0,3·0,8 = 0,14 + 0,24 = 0,38 (События  и
и  являются несовместными, а события A и
являются несовместными, а события A и  ,
,  и B – независимыми).
и B – независимыми).
б) Введем событие A - цель будет поражена, если стрелок произведет один выстрел из наугад выбранной винтовки.
Так как винтовки есть с оптическим прицелом и без оптического прицела, то введем две гипотезы:
H  - выстрел произведен из винтовки с оптическим прицелом,
- выстрел произведен из винтовки с оптическим прицелом,
H 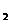 - выстрел произведен из винтовки без оптического прицела.
- выстрел произведен из винтовки без оптического прицела.
Искомую вероятность определим по формуле полной вероятности:
P (A) = P (H  )· P (A|H
)· P (A|H  ) + P (H
) + P (H 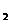 )· P (A|H
)· P (A|H 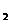 ).
).
Вероятность того, что выбрана винтовка с оптическим прицелом P (H  ) =
) = 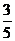 =0,6, а вероятность того, что выбрана винтовка без оптического прицела,
=0,6, а вероятность того, что выбрана винтовка без оптического прицела,  . По условию задачи, вероятность того, что стрелок поразит цель при выстреле из винтовки с оптическим прицелом P (A|H
. По условию задачи, вероятность того, что стрелок поразит цель при выстреле из винтовки с оптическим прицелом P (A|H  ) = 0,95, а для винтовки без оптического прицела эта вероятность P (A|H
) = 0,95, а для винтовки без оптического прицела эта вероятность P (A|H  ) = 0,7.
) = 0,7.
Тогда P (A) = 0,95·0,6 + 0,7·0,4 = 0,57 + 0,28 = 0,85.
в) В этой задаче требуется определить вероятность гипотезы уже после того, как событие уже совершилось. Для определения искомой вероятности надо воспользоваться формулой Бейеса. В нашем случае она имеет вид:

В этой формуле Н1, Н2, Н3 – гипотезы, что медведя убьет первый, второй и третий стрелок соответственно. До произведения выстрелов эти гипотезы равновероятны и их вероятность равна  .
.
A – медведь убит одной пулей.
P(H1/A) – вероятность того, что медведя убил первый стрелок при условии, что выстрелы уже произведены.
P(H2/A) – вероятность того, что медведя убил второй стрелок при условии, что выстрелы уже произведены.
P(H3/A) – вероятность того, что медведя убил третий стрелок при условии, что выстрелы уже произведены.
Вероятности того, что медведя убьет первый, второй или третий стрелок, вычисленные до выстрелов, равны соответственно:


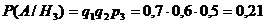
Здесь q1 = 0,7; q2 = 0,6; q3 = 0,5 – вероятности промаха для каждого из стрелков, рассчитаны как q = 1 – p, где р – вероятности попадания для каждого из стрелков.
Подставим эти значения в формулу Бейеса:

Задание 9.3. Решить задачу:
а) Вероятность того, что взятая наугад деталь из некоторой партии деталей, будет не бракованной равна 0,8. Найти вероятность того, что из 5 взятых деталей 2 окажутся не бракованными.
б) Найти вероятность того, что при 600 выстрелах мишень будет поражена ровно 250 раз, если вероятность поражения мишени при одном выстреле равна 0,4.
в) Вероятность совершить ошибку при наборе текста, содержащего 1500 знаков, равна 0,004. Какова вероятность того, при наборе было допущено ровно 5 ошибок?
Решение.
а) Так как p= 0,8 – не мало, а n = 5 - мало, то для вычисления искомой вероятности применим формулу Бернулли: P  = C
= C 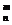 ·p
·p  ·q
·q  . В нашем случае: p= 0,8, q = 1 – 0,8 = 0,2, n = 5, m = 2. Тогда
. В нашем случае: p= 0,8, q = 1 – 0,8 = 0,2, n = 5, m = 2. Тогда 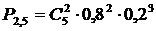 = =
= = 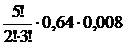 = 0,08.
= 0,08.
б) Так как число выстрелов n = 600 – велико, то воспользуемся приближен-ными формулами для вычисления искомой вероятности. Так как p = 0,4 > 0,1 и m = 250 – не мало, то в качестве приближенной формулы применим локальную теорему Муавра-Лапласа:
 , где
, где  =
= 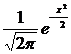 , x =
, x = 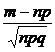 . Значения
. Значения  - функции Гаусса находятся по таблице. Находим
- функции Гаусса находятся по таблице. Находим  . По таблице определяем
. По таблице определяем  . Тогда по локальной теореме Муавра-Лапласа находим
. Тогда по локальной теореме Муавра-Лапласа находим 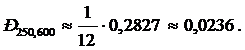
в) Так как n = 1500 – велико, то для нахождения требуемой вероятности воспользуемся приближенными формулами в схеме Бернулли. В нашей задаче m = 5 – мало, p = 0,004 < 0,1. Значит, более точный результат даст формула Пуассона:  , где
, где  = np. В нашем случае
= np. В нашем случае
 = 1500·0,004 = 6. Тогда
= 1500·0,004 = 6. Тогда 
 .
.
Задание 9.4. Решить задачу:
а) Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа каждого из приборов равны соответственно р1 = 0,3; p2 = 0,4; p3 = 0,5; p4 = 0,6. Найти закон распределения случайной величины X – числа отказавших приборов, а также математическое ожидание, дисперсию, среднее квадратическое отклонение и функцию распределения данной случайной величины.
б) Задана непрерывная случайная величина х своей функцией распределения плотностей вероятностей f(x):

Определить коэффициент a, найти функцию распределения, построить графики функции распределения и плотности распределения, определить вероятность того, что случайная величина х попадет в интервал 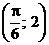 . Найти математическое ожидание и дисперсию заданной случайной величины.
. Найти математическое ожидание и дисперсию заданной случайной величины.
Решение.
а) Принимая за случайную величину X - число отказавших приборов, видим что эта случайная величина может принимать значения 0, 1, 2, 3 или 4.
Для составления закона распределения этой случайной величины необходимо определить соответствующие вероятности. Примем  .
.
1) Не отказал ни один прибор.

2) Отказал один из приборов.
 0,302.
0,302.
3) Отказали два прибора.

4) Отказали три прибора.
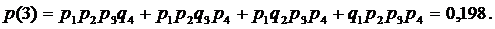
5) Отказали все приборы.

В итоге получаем закон распределения:
| x | |||||
| p | 0,084 | 0,302 | 0,38 | 0,198 | 0,036 |
Математическое ожидание случайной величины X найдем по формуле:  . Тогда
. Тогда 
Для нахождения дисперсии воспользуемся формулой:  .
.
Дополним закон распределения еще одной строчкой:
x 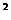
| |||||
| x | |||||
| p | 0,084 | 0,302 | 0,38 | 0,198 | 0,036 |
Тогда 
Соответственно 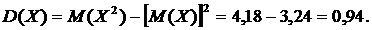
Среднее квадратическое отклонение  =
=  .
.
Функцию распределения F (x) найдем, используя определение: F (x) = P (X<x).
Если x  0, то F (x) = P (X<x) = 0;
0, то F (x) = P (X<x) = 0;
если 0 < x  1, то F (x) = P (X<x) = P (X = 0) = 0,084;
1, то F (x) = P (X<x) = P (X = 0) = 0,084;
если 1 < x  2, то F (x) = P (X<x) = P (X = 0) + P (X = 1) = 0,084 + 0,302 = 0,386;
2, то F (x) = P (X<x) = P (X = 0) + P (X = 1) = 0,084 + 0,302 = 0,386;
если 2 < x  3, то F (x) = P (X<x) = P (X = 0) + P (X = 1) + P (X = 2) = 0,084 + + 0,302 + 0,38 = 0,766;
3, то F (x) = P (X<x) = P (X = 0) + P (X = 1) + P (X = 2) = 0,084 + + 0,302 + 0,38 = 0,766;
если 3 < x  4, то F (x) = P (X<x) = P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3)= = 0,084 + 0,302 + 0,38 + 0,198 = 0,964;
4, то F (x) = P (X<x) = P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3)= = 0,084 + 0,302 + 0,38 + 0,198 = 0,964;
если x > 4, то F (x) = P (X<x) = P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3) + + P (X = 4) = 0,084 + 0,302 + 0,38 + 0,198 + 0, 036 = 1.
 0, если x
0, если x  0,
0,
0,084, если 0 < x  1,
1,
0,386, если 1 < x  2,
2,
Итак, F (x) = 0,766, если 2 < x  3,
3,
0,964, если 3 < x  4,
4,
1, если x > 4.
б) Найдем коэффициент a. Для этого воспользуемся формулой:  .
.
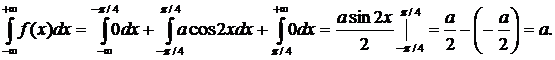
Поэтому a = 1.
Найдем функцию распределения F (x):
1) На промежутке  :
: 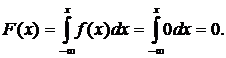
2) На промежутке 
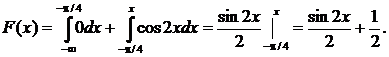
3) На промежутке 

Таким образом: 
Построим график плотности распределения:
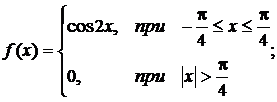

(На рисунке y = f (x)).
Построим график функции распределения:


(На рисунке y = F (x)).
Найдем вероятность попадания случайной величины в интервал 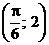 . Для этого воспользуемся формулами:
. Для этого воспользуемся формулами:
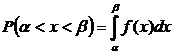 или
или  .
.
Тогда

(Соответственно, по другой формуле:
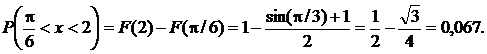 )
)
Определим математическое ожидание и дисперсию данной случайной величины: 
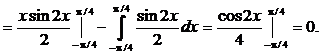

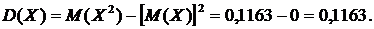
9.5. Для нахождения средней цены продовольственной корзины жителей сельской местности России было отобрано случайным образом 50 населенных пунктов. Полученные данные представлены в таблице:
| Стоимость продовольст- венной корзины, тыс. руб. | Менее 2 | 2 – 3 | 3 – 4 | 4 – 5 | 5 – 6 | 6 – 7 | 7 – 8 | Больше 8 | Итого |
| Число городов |
1. Постройте полигон и гистограмму относительных частот (частностей);
2. Найдите выборочную среднюю, дисперсию, «исправленную» выборочную дисперсию;
3. Найдите доверительный интервал для оценки с надежностью 0,95 неизвест-ного математического ожидания а нормально распределенного признака X генеральной средней.
4. Используя  - критерий Пирсона, на уровне значимости
- критерий Пирсона, на уровне значимости  = 0,05 проверить гипотезу о том, что случайная величина X – стоимость продовольственной корзины – распределена по нормальному закону.
= 0,05 проверить гипотезу о том, что случайная величина X – стоимость продовольственной корзины – распределена по нормальному закону.
Решение.
1. Для удобства вычислений построим следующую таблицу 1.
Таблица 1.
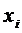
| 1,5 | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 | 7,5 | 8,5 |

| ||||||||

| 0,04 | 0,10 | 0,12 | 0,22 | 0,26 | 0,14 | 0,10 | 0,02 |
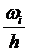
| 0,04 | 0,10 | 0,12 | 0,22 | 0,26 | 0,14 | 0,10 | 0,02 |
В качестве значений  берем средние значения из каждого интервала, при этом крайние интервалы (-∞; 2) и (8; +∞) заменяем на интервалы (1; 2) и (8; 9).
берем средние значения из каждого интервала, при этом крайние интервалы (-∞; 2) и (8; +∞) заменяем на интервалы (1; 2) и (8; 9).
Тогда полигон относительных частот будет следующий:


 0,28
0,28
 |
 0,24
0,24
 |
 0,20
0,20

 0,16
0,16

 0,12
0,12
 |  | ||
 0,08
0,08
 0,04
0,04
 |
0 1 2 3 4 5 6 7 8 9 10 
Гистограмма же относительных частот будет:




 0,28
0,28
 0,24
0,24
 |
 0,20
0,20


 0,16
0,16


 0,12
0,12
 | |||
 | |||
 0,08
0,08

 0,04
0,04
 |
0 1 2 3 4 5 6 7 8 9 10 
2. Для нахождения выборочного среднего воспользуемся формулой:
 ,
, 
Для вычисления выборочной дисперсии воспользуемся формулой
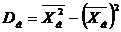 .
.
Найдем 
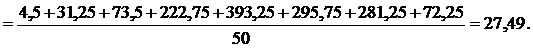
Тогда 
Так как исправленная выборочная дисперсия находится по формуле 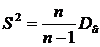 , то
, то 
Тогда исправленное среднее квадратическое отклонение 
Для нахождения доверительного интервала для оценки с надежностью 0,95 неизвестного математического ожидания а нормально распределенного признака X генеральной средней воспользуемся тем, что  ,
, 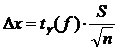 .
.
Тогда  Поэтому
Поэтому  .
.
4. Для проверки гипотезы о том, что случайная величина X – стоимость продовольственной корзины жителей сельской местности распределена по нормальному закону, составим таблицу 2.
Таблица 2.
| N | 
| 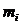
| 
| 
| 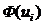
| 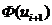
| 
| 
| 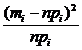
|
| 1 – 2 | |||||||||
| 2 – 3 | 5 7 | - ∞ | -1,05 | -0,5 | -0,3531 | 0,1469 | 7,345 |  0,02 0,02
| |
| 3 – 4 | -1,05 | -0,50 | -0,3531 | -0,1915 | 0,1616 | 8,08 |  0,54 0,54
| ||
| 4 – 5 | -0,50 | 0,04 | -0,1915 | 0,0160 | 0,2075 | 10,375 |  0,04 0,04
| ||
| 5 – 6 | 0,04 | 0,59 | 0,0160 | 0,2224 | 0,2064 | 10,32 |  0,70 0,70
| ||
| 6 – 7 | 0,59 | 1,14 | 0,2224 | 0,3729 | 0,1505 | 7,525 |  0,04 0,04
| ||
| 7 – 8 | 5 6 | 1,14 | +∞ | 0,3729 | 0,5 | 0,1271 | 6,355 |  0,02 0,02
| |
| 8 – 9 | |||||||||
| Ито-го | 1,0000 | 1,36 |
Для нахождения вероятности попадания значения случайной величины в нужный интервал, воспользуемся формулой  = Ф(
= Ф(  ) – Ф (
) – Ф ( ), где
), где
 =
=  , а
, а  =
=  . В качестве математического ожидания a возьмем
. В качестве математического ожидания a возьмем
 , а в качестве
, а в качестве 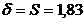 . Найдем все значения
. Найдем все значения  , затем используя Приложение 7 найдем Ф (
, затем используя Приложение 7 найдем Ф ( ), затем
), затем  , n
, n  .
.
Далее находим 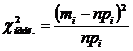 = 1,36
= 1,36  k = m – 3 = 3. Так как
k = m – 3 = 3. Так как  , то гипотезу
, то гипотезу  не отвергаем.
не отвергаем.