| Угол Ф-ция | 30̊ | 45̊ | 60̊ |
| sinα | 
| 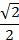
| 
|
| cosα | 
| 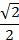
| 
|
| tgα | 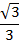
| 
|

Значения тригонометрических функций основных тригонометрических углов
| ||||||||||||||||||||||||||||||
| Окружность. Длина окружности, площадь круга. | 7. Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Формула длины окружности: C=2πR, где R – радиус. Формула площади круга: S = πR2, где R – радиус. | |||||||||||||||||||||||||||||
| Касательная к окружности. Центральные и вписанные углы. |
на которую он опирается:
Градусная мера вписанного угла равна половине градусной мере дуги, на которую он опирается:
| |||||||||||||||||||||||||||||
| Четыре замечательные точки треугольника | 2. Точка пересечения серединных перпендикуляров треугольника
Итак, мы рассмотрели первую замечательную точку треугольника – точку пересечения его серединных перпендикуляров.
3. Свойства биссектрисы угла
Если точка М лежит на биссектрисе угла, то она равноудалена от сторон угла, то есть расстояния от точки М до АС и до ВС сторон угла равны.
Теорема
Если точка равноудалена от сторон неразвернутого угла, то она лежит на его биссектрисе (см. Рис. 5).
Говорят, что биссектриса есть геометрическое место точек, равноудаленных от сторон угла.
Треугольник состоит из трех углов. Построим биссектрисы двух из них, получим точку О их пересечения (см. Рис. 6).
Точка О лежит на биссектрисе угла 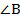 , значит, она равноудалена от его сторон АВ и ВС, обозначим расстояние за r: , значит, она равноудалена от его сторон АВ и ВС, обозначим расстояние за r: 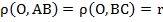 . Также точка О лежит на биссектрисе угла . Также точка О лежит на биссектрисе угла 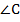 , значит, она равноудалена от его сторон АС и ВС: , значит, она равноудалена от его сторон АС и ВС: 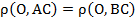 , , 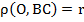 , отсюда , отсюда 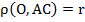 .
Несложно заметить, что точка пересечения биссектрис равноудалена от сторон третьего угла, а значит, она лежит на .
Несложно заметить, что точка пересечения биссектрис равноудалена от сторон третьего угла, а значит, она лежит на
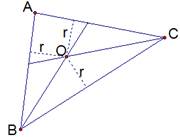 Рис. 6
биссектрисе угла
Рис. 6
биссектрисе угла 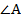 . Таким образом, все три биссектрисы треугольника пересекаются в одной точке.
Биссектрисы углов треугольника пересекаются в одной точке – центре вписанной окружности.
Итак, мы рассмотрели вторую замечательную точку треугольника – точку пересечения биссектрис.
Мы рассмотрели биссектрису угла и отметили ее важные свойства: точки биссектрисы равноудалены от сторон угла, кроме того, отрезки касательных, проведенных к окружности из одной точки, равны.
Третья замечательная точка треугольника – точка пересечения высот (или их продолжений) – ортоцентр.
Последняя замечательная точка – точка пересечения медиан.
Напомним, что три медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины. . Таким образом, все три биссектрисы треугольника пересекаются в одной точке.
Биссектрисы углов треугольника пересекаются в одной точке – центре вписанной окружности.
Итак, мы рассмотрели вторую замечательную точку треугольника – точку пересечения биссектрис.
Мы рассмотрели биссектрису угла и отметили ее важные свойства: точки биссектрисы равноудалены от сторон угла, кроме того, отрезки касательных, проведенных к окружности из одной точки, равны.
Третья замечательная точка треугольника – точка пересечения высот (или их продолжений) – ортоцентр.
Последняя замечательная точка – точка пересечения медиан.
Напомним, что три медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.
| |||||||||||||||||||||||||||||
| Вписанная и описанная окружности |
| |||||||||||||||||||||||||||||
| График показательной и логарифмической функции. |  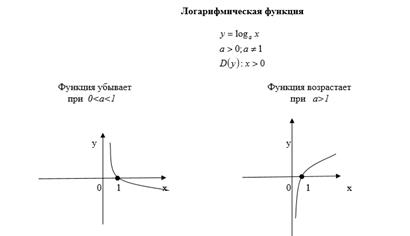
| |||||||||||||||||||||||||||||
| Табличные значения синуса, косинуса, тангенса и котангенса углов. |
| |||||||||||||||||||||||||||||
| Теорема синусов, теорема косинусов. | Теорема о площади треугольника.  
 Площадь треугольника равна Площадь треугольника равна 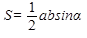 половине произведения двух его сторон
на синус угла между ними.
Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.
половине произведения двух его сторон
на синус угла между ними.
Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов. 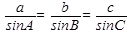
 Теорема косинусов.
Квадрат стороны треугольника равен
сумме квадратов двух других его сторон
Теорема косинусов.
Квадрат стороны треугольника равен
сумме квадратов двух других его сторон   минус удвоенное произведение этих сторон
минус удвоенное произведение этих сторон 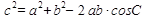  на косинус угла между ними.
на косинус угла между ними.
| |||||||||||||||||||||||||||||
| Векторы в двумерном и трехмерном пространствах. Основные понятия. Координаты вектора. Сложение и вычитание векторов. Угол между векторами. Длина вектора. Скалярное произведение векторов. Координаты середины отрезка. | Векторы
Определение 1.Вектором называется отрезок, для которого указаны начало и конец.
Определение 2.Коллинеарными называются векторы, лежащие на одной прямой либо на параллельных прямых. Коллинеарные векторы бывают сонаправленными и противоположно направленными.
Определение 3.Векторыназываются равными, если они сонаправлены, и их длины равны.
Определение 4.Векторыназываются противоположными, если они противоположно направлены, и их длины равны.
Определение 5.Компланарными называются векторы, которые, будучи отложенными от одной точки, лежат в одной плоскости.
Определение 6.Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними. 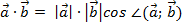 Правила действий с векторами.
Правила действий с векторами.
Умножение вектора на число. Произведением вектора
Основные формулы метода координат. Пусть A 1) Координаты вектора 2) Координаты середины отрезка АВ: ( 3) Расстояние между точками А и В (длина АВ): 4) Скалярное произведение векторов
| |||||||||||||||||||||||||||||
| Арифметическая и геометрическая прогресии. Рекурентная формула, формула n-го члена, формула суммы n первых членов. |
| |||||||||||||||||||||||||||||
| Скрещивающиеся прямые. Признак параллельности прямой и плоскости, признак параллельности двух плоскостей, признак скрещивающихся прямых | 1. Скрещивающимися называются прямые, не лежащие в одной плоскости. 2. Признак скрещивающихся прямых: Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые являются скрещивающимися. 3. Чтобы найти угол между скрещивающимися прямыми, надо - перенести одну из прямых параллельно так, чтобы она проходила через точку на второй прямой - найти угол между получившимися пересекающимися прямыми (0o < α ≤ 90̊) 4. Параллельными плоскостяминазываются плоскости, не имеющие общих точек. 5. Признак параллельности плоскостей:Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то такие плоскости параллельны. | |||||||||||||||||||||||||||||
| Иррациональные уравнения. Показательные уравнения и неравенства. | 1. Иррациональные уравнения –уравнения, в которых неизвестное находится под знаком корня.
Для решения иррационального уравнения нужно возвести в соответствующую степень обе части уравнения. При этом получается уравнение – следствие, необходимо делать проверку полученных решений.
2.
3.
Поиск по сайту©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-04-27 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |