Вопрос 1
· Функция и аргумент. Способы задания функциональной зависимости.
Функция - это Соответствие между двумя множествами при котором каждому элементу ервого множества по определенному закону или правилу соответствует не более одного множества. Аргумент функции — независимая переменная, от значений которой зависят значения функции. Способы задания функцион зависимости:Аналитический способФункция задается в виде аналитического выражения или формулы, содержащей указания на операции или действия над константами и аргументом x, чтобы получить соответствующие значения y. Табличный способАргумент и вычисляемая функция записываются в таблицу. Форма таблицы может быть вертикальной или горизонтальной.Графический способГрафический способ задания функции является наиболее наглядным и часто применяется в технике. Самописцы и многоканальные шлейфовые осциллографы дают изображение графика (графиков) на бумагу, например, с датчиков, установленных на теле человека при снятии электрокардиограммы сердца. Электронные осциллографы выдают изображение графика на экран электронно-лучевой трубки.
Вопрос 2
· Производная функции как мера скорости процесса. Градиенты.
· Мгновенная скорость есть предел отношения приращения пути к приращению времени, когда приращение времени стремится к нулю. Если функция описывает какой-либо физический процесс, то производная есть скорость протекания этого процесса. Производная функции y=f(x) по аргументу х есть мгновенна скорость изменения функции y=f(x): 
.
· Градиент
Градиент - вектор, показывающий направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой
Вопрос 3
· Геометрический смысл производной.
Производная в точке x0 равна угловому коэффициенту касательной к графику функции в точке с абсциссой x0.
Механическийсмысл
Производная функции 
по аргументу x есть мгновенная скорость изменения функции : 
.
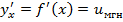Вопрос 4
· Основные правила дифференцирования и производные элементарных функций.
Процесс нахождения производной называется дифференцированием. Функция y=f(x) называется дифференцируемой в точке x, если ее приращение в этой точке можно представить в виде: дельта y = A дельта x+a(дельта x)дельта x. Для того, чтобы функция была дифференцируемой в точке x, необходимо и достаточно, чтобы она имела в этой точке производную. 1) выбрав нек знач х, дают ему приращение дельта х и находят значение функции в точке х+ дельта х, равное f(x+rx), 2) определяют приращение функции: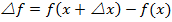 
, 3) составляют отношение rf/rx и если возможно упрощают его, 4) находят производную функции, т.е. предел 
, если этот предел существует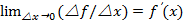 
. Производная функции: 1) f(x+rx)=x+rx, 2) rf=x+rx-x=rx, 3) rf/rx=rx/rx=1, 4) 
, следовательно 
Вопрос 5
· Производные высших порядков.
Производная у'=ƒ'(х) функции у=ƒ(х) есть также функция от х и называется производной первого порядка. Если функция ƒ'(х) дифференцируема, то ее производная называется производной второго порядка и обозначается у". Итак, у"=(у')'.Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'" (или ƒ'"(х)). Итак, у'"=(y")'Производной n-го порядка (или n-й производной) называется производная от производной (n-1) порядка:y(n)=(y(n-1)).Производные порядка выше первого называются производными высших порядков.Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (уν или у(5)— производная пятого порядка).
Вопрос 6
· Применение производных для исследования функций на экстремум.Экстре́мум в,,математике - максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализевыделяют также понятие локальный экстремум (соответственно минимум или максимум).
Вопрос 7
· Дифференциал функции. Дифференциалом функции y=f(x) в точке x называется главная (линейная) часть ее приращения, равная произведению производной функции на приращение аргумента.dy=df= 
. Аналитический смысл дифференциала – дифференциал функции есть главная часть приращения функции rf, линейная относительно прира щения аргумента rx. Дифференциал функции отличается от приращения функции на бесконечно малую более высокого порядка малости, чем rх. Дифферинциал аргумента dx = его приращению rх: dx=rx. Выражение производной через дифференциал функции и дифференциал агрумента: 
Вопрос 8
· Применение дифференциального исчисления в приближенных вычислениях. Пусть мы имеем функцию u=f(x,y). Определяя значения х и у мы допускаем погрешность дельта х и дельта у. Тогда значение u также получится с погрешностью дельта u=f(x+rx,y+r у) – f(x,y))
Вопрос 9
· Функции двух и нескольких переменных. Состояние организма как функция многих переменных. Определение. Если каждой паре (x, y) значений двух независимых переменных из области ставится определенное значение z, то говорят, что z есть функция двух переменных (x, y). Z=f(x,y). Геометрическое изображение функции двух переменных - поверхность.Частное и полное приращение функции. Полное приращение функции дельта z = f(x+дельта x, y+ дельта у) – f(x,y)/ Частное приращение ф ункции дельта z по x = f(x+rx)-f(x,y)
Вообще, полное приращение функции не равно сумме частных приращений. Пример. z = xy. дельта z по x =(x+ дельта x)y-xy=y дельта x, дельта z по y=x(y+ дельта y) – xy =x дельта y.
Вопрос 10
· Частные производные и полный дифференциал функции нескольких переменных. Для функции двух переменных z=f(x,y) частной производной по переменной x назыв производная этой функции по x при постоянной у. Для функции двух переменных z=f(x,y) частной производной по переменной y назыв производная этой функции по y при постоянной x.Если функция z= f (x y) дифференцируема в точкеP0(x0,y0), тоглавная, линейная относительно приращения аргументов, часть ее полного приращения называется полным дифференциалом функции. Произведение 
dx называют частным дифференциалом функции f(x,y) по х и обозначают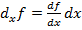 
. Сумму частных дифференциалов функции z=f(x, y) называют ее полным дифференциалом и обозначают df= 
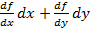. Полный диффер функции многих независимых переменных = сумме частных дифференциалов: df= 
Вопрос 11
· Первообразная функция и неопределенный интеграл.
Зная закон движения тела, можно, продифференцировав функцию перемещения тела по времени, в любой момент найти его скорость. Часто требуется решить обратную задачу, то есть найти перемещение тела, зная, как изменяется его скорость. Эта и подобные задачи решаются при помощи интегрирования – операции, обратной дифференцированию.
Функция F, заданная на некотором промежутке D, называется первообразной функции f, заданной на том же промежутке, если для любого x?D. Fштрих(x)=f(x)
Так, функция f=x3/3 является первообразной функцииf(x) =x2 в чем можно убедиться, поставив эти функции в определение первообразной. Функция f=x3/3+1 также является первообразной функции f(x)=x2. Если функция F является первообразной функции f, то все функции вида F + C, где C – константа, и только они являются первообразными функции f. Таким образом, для любой функции ее первообразная F определяется неоднозначно. Для того, чтобы задать ее однозначно, нужно указать точку A (x 0; y 0), удовлетворяющую уравнению y = F (x). Неопределенным интегралом от функции называется множество всех первообразных этой функции.Всякая непрерывная функция на интервале имеет на этом интервале первообразную, а значит и неопределенный интеграл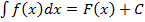 
. Всякая непрерывная функция на интервале имеет на этом интервале первообразную, а значит и неопределенный интеграл.
Вопрос 12
· Основные свойства неопределенного интеграла. Основные формулы интегрирования. Производная от неопределенного интеграла равна подынтегральной функции. 
Дифференциал от неопределенного интеграла равен подынтегральному выражению.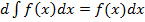 
.. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной константы. 
. Постоянный множитель можно выносить за знак интеграла.. Неопределенный интеграл от суммы конечного числа функций равен сумме интегралов от слагаемых функций. 
, 
, 
, 
, 
, 
, 
, 
.
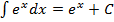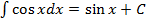Вопрос13
· Методы нахождения неопределенных интегралов (приведение к табличному виду, метод замены переменной, интегрирование по частям).
Замена переменной: пусть функция х=фи от t определена диффиринцируема на промежутке t и x – множество её значений, функция y=f(x) определена на множестве x и имеет на это множество первообразную, тогда: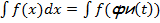 
* фи штрих от tdt. Метод интегрирования по частям: Пусть функции u=u от x и v= v от x дифференцируемы на промежутке х, существует 
Тогда существует интеграл 
. И справедлива формула: 
.
Вопрос 14
· Определенный интеграл. Свойства определённого интеграла. Если интегральная сумма имеет предел I, который не зависит ни от способа разбиения отрезка (a,b), ни от выбора точек Z, то этот предел называется определенным интегралом от функции y=f(x) на отрезке (a,b) и обозначается 
Cв-ва:1) Определенный интеграл не зависит от обозначения переменной интегрирования, т.е. 
2) Определенный интеграл от суммы конечного числа непрерывных функций заданных на отрезке (a,b) равен сумме определенных интегралов от слагаемых функций: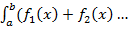 
= 
3) Постоянный множитель R подынтегральной функции можно выносить за знак определенного интеграла: 
dx=R , 4) Если верхний и нижний пределы интегрирования поменять местами, то определенный интеграл сохранит абсолют величину и изменит свой знак на противоположный: 
, 5) 
Вопрос 15
· Применение определенного интеграла к вычислению площадей фигур и работы переменной силы. Пусть функция f(x) непрерывна на участке [a,b]. Если f(x)>0, то площадь криволинейной трапеции, ограниченной линиями y=f(x), y=0, x=a, x=b, численно равна интегралу S= 
.Если f(x)≤0, то площадь ровна S= 
. Если кривая f(x) пересекает ось 0х, то отрезок [a,b] нужно разбить на части, в пределах которых f(x) не меняет знака. К каждой части применяют интегрирование и сумма частей будет равна площади.
Пусть материальная точка М перемещается вдоль оси Ох под действием переменной силы F = F(х), направленной параллельно этой оси. Работа, произведенная силой при перемещении точки М из положения х = а в положение х = b (а <bЬ), находится по формуле
A = 
Пример. Какую работу нужно затратить, чтобы растянуть пру-'—' жину на 0,05 м, если сила 100 Н растягивает пружину на 0,01 м?[5]
Решение: По закону Гука упругая сила, растягивающая пружину, пропорциональна этому растяжению х, т. е. F = kх, где k — коэффициент пропорциональности. Согласно условию задачи, сила F = 100 Н растягивает пружину на х = 0,01 м; следовательно, 100 = k 0,01, откуда k = 10000; следовательно, F =10000х.
Искомая работа на основании формулы
равна
A = = 
=5000x2│0.050=12.5 Дж
Вопрос 16
· Связь между определенным и неопределенным интегралами. Правило Ньютона-Лейбница.
при совпадении пределов интегрирования интеграл обращается в нуль, то сразу увидим, что 
, Отсюда вытекает, что 
и потому 
В частности, при x = b находим: 
Эта формула (называемая формулой Ньютона-Лейбница) сводит вопрос о вычислении определенного интеграла любой непрерывной функции к нахождению для нее первообразной функции. По существу этим перекинут мост между двумя частями математического анализа - дифференциальным исчислением (к которому, собственно, надо отнести и понятие первообразной функции) и интегральным исчислением, которое изучает в основном пределы интегральных сумм. К концу XVII в. оба эти исчисления были разработаны уже весьма обстоятельно, но то, что они связаны между собой, еще не было выяснено. Заслугой Ньютона и Лейбница является именно установление факта этой связи. Видим, что в основе ее лежит предложение, составляющее содержание теоремы, почему мы и назвали эту теорему основной теоремой математического анализа. Ввиду чрезвычайной важности установленного результата придадим ему форму следующего правила: Правило. Для вычисления определенного интеграла от непрерывной функции надо найти для нее первообразную функцию и составить разность значений этой последней функции при верхнем и нижнем пределах интегрирования.
Вопрос 18
· Этапы решения задач при использовании дифференциальных уравнений. 1.Перевод условий на язык математики. 2.Решение задачи. 3. Оценка результатов.
Вопрос 17
· Понятие об обыкновенных дифференциальных уравнениях.
Дифференциальное уравнение - это уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значения её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, ее производные и независимые переменные.
Все дифференциальные уравнения можно разделить на обыкновенные дифференциальные уравнения (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Порядком или степеньюдифференциального уравнения называется наибольший порядок производных, входящих в дифференциальное уравнение.
Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени. Формулировка второго закона Ньютона для материальной точки дает простейший пример обыкновенного дифференциального уравнения второго порядка с неизвестной функцией координат точки и временем, выступающим в роли независимой переменной.
Обыкновенное дифференциальное уравнение (ОДУ) -ого порядка — это уравнение вида 
где y=y(x) — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной x, штрих означает дифференцирование по x.
Решением дифференциального уравнения называется n раз дифференцируемая функция y(x), удовлетворяющая уравнению во всех точках своей области определения. Обычно существует целое множество таких функций (такое параметризованное семейство рещений называется общим решением дифференциального уравнения), и для выбора одного из них требуется наложить на него дополнительные условие: например, потребовать, чтобы решение принимало в данной точке данное значение. Полученное единственное решение называется частным решением. Общее решение обыкновенного дифференциального уравнения n -ого порядка может быть выражено в виде Y=f(x,C1,Cn))
Вопрос 19
· Дифференциальные уравнения первого порядка с разделяющимися переменными. Общие и частные решения дифференциальных уравнений.
Простейшие дифференциальные уравнения первого порядка — класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию. К нему относятся уравнения в полных дифференциалах, уравнения с разделяющимися переменными, однородные уравнения первого порядка и линейные уравнения первого порядка. Все эти уравнения можно проинтегрировать в конечном виде. eсли в уравнении P(t,x)dt + Q(t,x)dx=0: P(t,x) T1(t)X1(x), Q(t,x) = T2(t)X2(x), то это уравнение с разделяющимися переменными. Частным решением дифференциального уравнения на интервале (альфа бетта) называется каждая функция y(x), которая при подстановке в уравнение вида обращает его в верное тождество на интервале (альфа бетта). Зная общее решение однородного дифференциального уравнения и любое частное решение неоднородного уравнения, можно получить общее решение неоднородного уравнения в виде суммы общего решения однородного уравнения и частного решения неоднородного.
Вопрос 20
· Составление и решение дифференциальных уравнений первого порядка на примерах задач медико-биологического содержания: закон растворения лекарственных форм вещества из таблетки, закон размножения бактерий и др. Скорость растворения лек. форм в-ва таблетки пропорциональна количеству лек. форм в-ва в таблетке. Пусть m-кол-во в-ва в таблетке,оставшееся ко времени растворения t. Тогда dm/dt=-km. K- константа скорости растворения. Разделим и прологарифмируем уравнение. В итоге m= 
. Отсюда выражают k= 
.
· З-н размнож. бакт. Скорость размножения некоторых бакт пропорциональна кол-ву бакт в данный момент.dx/dt=-kx, x= 
(х-кол-во бакт в данный момент).
Вопрос 24
• Законы распределения дискретных и непрерывных случайных величин.Законом распределения дискретной случайной величины наз.соответствие между ее возможными значениями и их вероятностями.Закон распределения дискретной случайной величины может быть задан в виде таблицы.Такая таблица может быть конечной или бесконечной.Также таблицы в которых указанны значения случайной величины и их вероятности, называют рядом распределения.(Для придания ряду распределения более наглядного вида используют его графическое изображение).
Вопрос 21
Законы сложения и умножения вероятностей.Теорема сложения. Сумма двух событий А и В называют событие С=А+В, заключающееся в наступлении события А, или события В, или событий А и В одновременно. Суммой нескольких событий называют событие, которое состоит в осуществлении хотя бы одного из этих событий. Событие А+В+С заключается в осуществлении хотя бы одного из следующих событий: А,В,С, А и В, А и С, В и С, А и В и С. Теорема. Вероятность наступления одного из двух несовместимых событий А и В равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В). Теорема. Сумма вероятностей несовместимых событий, образующих полную группу событий, равна единице. Противоположные события. Два события наз. противоположными, если они несовместны и образуют полную группу.Если событие обозначают А, то противоположное событие обозначают А. Законы умножение вероятностей. (Бывают зависимые и независимые). Два события А и В наз.независимыми, если вероятность осуществления события А не зависит от того, как осуществилось событие В или нет. Теорема.Вероятность произведения двух независимых событий А и В равна произведению вероятностей этих событий:Р(А+В)=Р(А)*Р(В). Событие В наз.зависимым от события А,если вероятность осуществления события В зависит от того,осуществилось или нет событие А.Теорема. Вероятность произведения двух независимых событий А и В равна произведению одного из них на условную вероятность второго, вычисленную при условии, что первое событие осуществилось: Р(АВ)=Р(А)*Р(В/А).Формула Бернулли:Р=n/m(n-m) p^m q^(n-m),где р-вероятность осуществления события,q-противоположного,n-независимые повторные испытания,m-кол-во раз.
Вопрос 20
· Случайное событие, вероятность случайного события. Случа́йное собы́тие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности. Случайное событие, которое никогда не реализуется в результате случайного эксперимента, называется невозможным и обозначается символом перечеркнутый круг. Случайное событие, которое всегда реализуется в результате случайного эксперимента, называется достоверным и обозначается символом Ω. Математически случайное событие — подмножество пространства элементарных исходов случайного эксперимента; элемент алгебры или сигма-алгебры событий F, которая в свою очередь задаётся аксиоматически и вместе с пространством элементарных событий Ω и вероятностью P образует вероятностное пространство Ω, F,P..
Вероятность случайного события Событие называется случайным, если в результате испытания (опыта) оно может произойти, а может и не произойти. Примеры. Испытание бросание монеты, случайное событие выпадение герба. Испытание участие в игре Русское лото, случайное событие - выигрыш. Испытание прыжок с парашютом, случайное событие удачное приземление. Испытание рождение ребенка, случайное событие пол ребенка мужской. Испытание наблюдение за погодой в течение дня, случайное событие в течение дня был дождь. Как видим наступление случайного события в результате испытания, вообще говоря, нельзя предсказать заранее в принципе. Этот факт непредсказуемость наступления можно в некоторых случаях считать главным отличительным свойством случайного события. Тем не менее, имеется возможность некоторые случайные события подвергнуть анализу методами математики. Пусть некоторое испытание произведено раз и в результате этого связанное с ним случайное событие (обозначим его через А) произошло раз. Тогда относительной частотой случайного события А, назовем отношение к. Другими словами. Для многих случайных событий относительная частота обладает свойством устойчивости, то есть в различных длинных серия испытаний относительные частоты одного и того же случайного события мало отличаются друг от друга. Случайные события, относительные частоты которых, обладают свойством устойчивости, называются регулярными. Устойчивость относительной частоты была обнаружена и многократно подтверждена экспериментально естествоиспытателями в 17-19 веках. Наиболее впечатляющим является результат К. Пирсона, который бросал монету 12000 раз, затем осуществил еще одну серию бросаний 24000 раз. В этих сериях он подсчитывал количество выпадений герба и получил значения относительной частоты для него 0,5016 и 0,5005, отличающиеся друг от друга на 0,0011. Для случайных событий обладающих свойством устойчивости, относительную частоту наступления
Вопрос 22
· Дискретные и непрерывные случайные величины. Величину,которая в результате испытания примет только одно возможное значение,наз.случайной.Случайные величины обозначают большими буквами латинского алфавита, а их значения маленькими.Вероятность случайных величин обозначают буквами с соответствующими им индексами:Р(Х= 
)=Р()= 
и т.д.Дискретной(прерывной)наз.случайную величину,принимающую отдельные друг от друга возможные значения с определенными вероятностями,которые можно пронумеровать.Число возможных значений дискретной случайной величины может быть конечным и бесконечным.Непрерывной наз.величину,которая может принимать все значения из некоторого конечного или бесконечного интервала.Число возможных значений непрерывной случайной величины бесконечно.
Вопрос 25
· Числовые характеристики случайных величин:математическое ожидание,мода,медиана,дисперсия,среднее квадратическое отклонение. Математическим ожиданием дискретной случайной величины Х называется сумма произведений всех возможных значений величины Х на вероятности этих значений:М(Х)= 
. Свойства матем.ожид.:1.Математическое ожидание постоянной величины С равно этой постоянной:М(С)=С. 2.Постоянный множитель С можно выносить за знакматематического ожидания:М(СХ)=СМ(Х). 3.Математическое ожидание алгебраической суммы случайных величин равно алгебраической сумме их математических ожиданий:М(X 
Y)=М(X) М(Y).
Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:M(XY)=M(X)*M(Y).Модой дискретного распределения называют такое значение 
случайной величины,что предшествующее и следующее за ним значения имеют вероятности, меньше Р().Дисперсией дискретной случайной величины называют математическое ожидание квадрата разности случайной величины Х и ее математического ожидания µ.Дисперсию обозначают D(X) или 
.D(Х)= 
µ).Свойства дисперсии случ.величины:1.Дисперсия постоянной величины С равна 0. 2.Постоянный множитель можно выносить за знак дисперсии,возводя его в квадрат:D(СХ)= 
D(Х). 3.Дисперсия двух независимых случайных величин равна сумме дисперсий этих величин:D(X+Y)=D(X)+D(Y). 4.Дисперсия разности двух независимых величин X и Y равна сумме их дисперсий:D(X-Y)=D(X)+D(Y).Средним квадратическом отклонением случайной величины называют корень квадратный из ее дисперсии.
Вопрос 26
· Примеры различных законов распределения. Нормальный закон распределения. Непрерывная случайная величина Х имеет равномерное распределение вероятностей на отрезке 
,если ее плотность вероятности на 
a,b 
постоянна, а вне равна нулю.Нормальный закон распределения(закон Гаусса).Закон распределения вероятностей непрерывной случайной величины Х называют нормальным,если плотность вероятности определяется формулой: f(x)=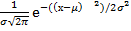 
,где 
- соответственно среднее квадратическое отклонение и математическое ожидание случайной величины Х.
Вопрос 27
· Задачи математической статистики. Математическая статистика – раздел прикладной математики, примыкающий к теории вероятностей. В математической статистике рассматриваются приближенные методы отыскания законов и характеристик по результатам экспериментов. Разработка методов регистрации, описания и анализа экспериментальных данных составляют предмет математической статистики. На практике результаты наблюдений и обработки содержат больший или меньший элемент случайности. При этом нужно определить, какие черты наблюдаемого явления относятся к постоянным, а какие являются случайными.
· Выборочный метод. Генеральная совокупность и выборка.
Совокупность, состоящая из всех объектов, которые могут быть к ней отнесены, наз.генеральной.Число объектов генеральной совокупности называют ее объемом и обозначают N. Множество объектов, случайно отобранных из генеральной совокупности, наз.выборочной совокупностью или выборкой. Число объектов выборки наз.ее объемом и обозначают n.В зависимости от техники отбора объектов из генеральной совокупности выборки делятся на повторные и бесповторные. Если выборку отбирают по одному объекту, который обследуют и снова возвращают в генеральную совокупность, то выборка наз.повторной.Если объекты выборки не возвращаются в генеральную совокупность, то выборка наз.бесповторной.
Вопрос 28
· Статистическое распределение (дискретный и интервальный ряд распределения).Полигон и гистограмма. Наблюдаемые значения признака х1,х2, …, хk называют вариантами, а последовательность вариант,записанную в возрастающем порядке,-вариационным рядом.p= 
.Таблицу,содержащую значения вариант признака и их частоты или относительные частоты, называют статистическим дискретным рядом распределения или статистическим распределением выборки. В случае большого количества вариант и непрерывного распределения признака статистическое распределение признака можно задать в виде последовательности интервалов и соответствующих им частот или относительных частот. p=m/n. Таблицу,содержащую частичные интервалы и их частоты или относительные частоты,называют статистическим интервальным рядом распределения.Для графического изображения статистического распределения используются полигоны и гистограммы.Полигон-ломаная,отрезки которой соединяют точки.Гистограмма-ступентчатая фигура,состоящая из прямоугольников.
Вопрос 29
· Эмпирическая ф-ция распределения. Эмпирической ф-цией распределения называют ф-цию F*(x),определяющую для каждого значения х относительную частоту события Х 
: F*(x)=m(x)/n,где m(х) чисто наблюдений, при которых значение признака Х меньше х;n-объем выборки.В отличии от эмпирической ф-ции распределения F*(x) выборки ф-цию распределения F(x) генеральной совокупности называют теоретической ф-цией.Различие между эмпирической F*(x) и теоретической F(x) ф-циями состоит в том, что F(x) определяет вероятность события Х х, F*(x)-относительную частоту этого же события.Поэтому эмпирическую ф-цию распределения выборки F*(x) можно использовать для приближенного представления теоретической ф-ции распределения генеральной совокупности.Ф-ция F*(x) облад.свойствами:1.Значения эмпирической ф-ции принадлежат отрезку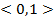 
.2. F*(x)-неубывающая ф-ция.
Вопрос 30
· Выборочные характеристики и точечные оценки характеристик генеральной совокупности:выборочная средняя,оценка дисперсии,оценка среднеквадратического отклонения(стандартное отклонение), оценка среднеквадратического отклонения выборочной средней(ошибка среднего). Точечной называют оценку,которая определяется одним числом.Для того чтобы оценка давала хорошее приближение,она должна удовлетворять определенным требованиям:быть несмещенной,эффективной и состоятельной.Точечная оценка 
*параметра наз.несмещенной,если ее математическое ожидание равно оцениваемому параметру при любом объеме выборки,т.е.М( *)= .Оценку,математическое ожидание которой не равно оцениваемому параметру,наз.смещенной.За меру точности несмещенной оценки * для параметра принимают дисперсиюD( *).Оценку с наименьшей дисперсией наз.наилучшей.Эффективность-отношение дисперсий наилучшей оценки и данной несмещенной оценки.Примером состоятельной оценки явл.любая несмещенная оценка,дисперсия которой при n 
стремиться к нулю.Выборочной средней наз.среднее арифметическое значений х1,х2,…,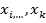 
признака выборочной совокупности: х= 
/n.Оценка дисперсии: 
= 
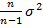.Оценка среднеквадратического отклонения: 
Вопрос 31
Доверительным интервалом называется интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром, такой, что он содержит данный параметр с заданной вероятностью α.Наиболее распространенным является оценка математического ожидания a случайной величины X, распределенной по нормальному закону, при известном среднем квадратическом отклонении σ. В этом случае для оценки математического ожидания a служит интервал: 
, t 
где 
– точность оценки, n – объём выборки, – выборочное среднее, t – аргумент функции Лапласа.
Вопрос 32
· Оцкнка случ погрешн при прямых и косвен измерениях. Случайными наз неопределенные по вел-не и природе погрешности измерений,зависящие от измерительного устройства и внешних условий(вибрация, колебания температуры,..) По форме представления Абсолютная погрешность — Δ X является оценкой абсолютной ошибки измерения. Величина этой погрешности зависит от способа её вычисления, который, в свою очередь, определяется распределением случайной величины Xmeas. При этом неравенство: Δ X > | Xmeas − Xtrue |, где Xtrue — истинное значение, а Xmeas — измеренное значение, должно выполняться с некоторой вероятностью, близкой к 1. Если случайная величина Xmeas распределена по нормальному закону, то обычно за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина. Относительная погрешность — погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или