Рассмотрим полностью целочисленную задачу линейного программирования (13.4) – (13.7), в которой n 1 = n.
Пусть 
– оптимальный опорный план задачи 
на целочисленность. Если они все целые, то 
. Если хотя бы одна координата, допустим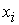 
, будет нецелой, поступим следующим образом.
Обозначим через N совокупность небазисных переменных и на основании последней симплексной таблицы выразим целевую функцию и все переменные 
через небазисные переменные 
:
. (13.10)
Так как 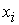– нецелая величина, обозначим ближайшее целое число, не превосходящее 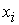, через [ 
] (целая часть 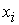) и определим дробную часть числа ({ }):{ }= – 
.
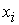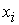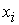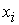Очевидно, { 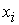}>0.
Теорема 13.5. Пусть 
– допустимое решение задачи 
. Тогда соотношение
,
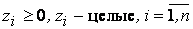(13.11)
определяют правильное отсечение.
Доказательство. Запишем выражение (13.10) в виде
Используя выражение (13.11), получим
или
.
На основании предположения теоремы о допустимости решения задачи 
– целые. Величины 
целые по определению. Следовательно, 
тоже целое.
Докажем, что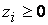 
. Предположим, что 
. Это значит, что
.
По определению дробной части 
. По условию теоремы x – допустимое решение задачи , поэтому 
. Следовательно, 
, 
. Отсюда 
, или, что то же самое, 
. Итак, – нецелое, а это противоречит только что доказанному. Следовательно, предположение неверное. Теорема доказана.
Следствие. Любое оптимальное решение X(D, F) задачи (D, F), не являющиеся допустимым решением задачи не удовлетворяет условию правильного отсечения (13.11).
Доказательство. Пусть X (D, F) – оптимальное решение задачи (D, F), 
–дробное. Покажем, что не удовлетворяет условию отсечения. Из оптимальности плана следует, что 
. Поэтому 
. Учитывая это, подставим в выражение (13.11):
что противоречит условию .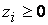
Важной проблемой метода отсечения является нарастание количества дополнительных ограничений по мере решения вспомогательных задач, оптимальные планы которых будут содержать нецелые координаты, т.е. возникает проблема размерности. Гомори предложил прием, ограничивающий размеры рассматриваемых расширенных симплексных таблиц числом (n +2)(k +1), где n – количество переменных задач 
, k – число ее небазисных переменных. Этот прием основан на том, что дополнительные ограничения (правильные отсечения) 
интересуют нас лишь как способ отсечения нецелочисленного оптимального решения 
и перехода от задачи 
к задаче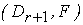 
. Заметим, что переменная 
выводится из базиса сразу же после введения ограничения:
,
.
Идею Гомори проиллюстрируем на конкретном примере.
Пример. Решить полностью целочисленную задачу линейного программирования:
максимизировать 
при условиях
Отбрасывая условие целочисленности, решаем задачу симплексным методом.
Решение задачи :
| Номер итерации | Базисные переменные |
| 
| 
| 
| 
| 
| |||||||||
|
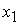
| -1 | |||||||||||||||
|
| ||||||||||||||||
| F | -7 | -9 | ||||||||||||||
| I |
| -1/3 | 1/3 | – | ||||||||||||
|
| 22/3 | -1/3 | 9/2 | |||||||||||||
| F | -10 | |||||||||||||||
| II |
| 7/2 | 7/22 | 1/22 | ||||||||||||
|
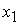
| 9/2 | -1/22 | 3/22 | |||||||||||||
| F | 28/11 | 15/11 | ||||||||||||||
После II итерации получаем в последней симплексной таблице оптимальное решение 
. Это решение не целочисленное. Поэтому переходим к построению задачи 
. С нецелочисленным значением 
две строки – первая и вторая. Номер k выбираем из условия
.
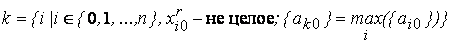В нашем случае 
. Тогда для образования сечения выбирается первая строка, т.е. k = 1. Запишем первое сечение Гомори:
.
Так как {7/2} = 1/2, {7/22} = 7/22, {1/22} = 1/22, получаем
.
Перенеся члены с переменными в правую часть и введя неотрицательную балансовую переменную 
, получим сечение в форме 3-го дополнительного уравнения 
. (13.12)
Присоединив его к предыдущим двум, придем к задаче 
. Ее решение можно начинать с окончательной симплексной таблицы для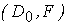 
, добавив уравнение (13.12).
Решение задачи :
| Номер итерации | Базисные переменные |
|
|
|
|
| 
| 
| 
|
|
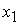
| 7/2 | 7/22 | 1/22 | ||||||
|
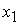
| 9/2 | -1/22 | 3/22 | – | 11/3 | ||||
|
| 1/2 | 7/22 | 1/22 | -1 | 11/7 | ||||
| F | 28/11 | 15/11 | |||||||
| I |
| -1 | |||||||
|
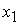
| 32/7 | 1/7 | -1/7 | ||||||
|
| 11/7 | 1/7 | -22/7 | ||||||
| F |
В уравнении (13.12) переменная может быть базисной, однако коэффициент при ней равен –1, поэтому в исходной для задачи таблице базисное решение не является опорным 
. Значит, необходимо получить исходное опорное решение.
Выделим третью дополнительную строку и для столбцов, имеющих в ней положительные элементы (в нашем случае для 3-го и 4-го), вычислим отношения 
. Если найдется столбец, для которого min{ } соответствует выделенной строке, то данные столбец и строку выбираем в качестве разрешающих, после чего переменная сразу же выводится из базиса и новое решение становится опорным. Если такого столбца нет, то в качестве разрешающих выбираются столбец с наименьшим элементом в выделенной строке и строка по min{ }. После этого начинается процесс преобразования симплексной таблицы.
В данном случае min{ } соответствует выделенной строке 3-го столбца. Поэтому, выбрав за разрешающие 3-ю строку и 3-й столбец, сразу получим опорное решение, которое одновременно и оптимально: 
. Так как оно опять не целочисленное, то перейдем к построению задачи 
.
Соответствующие сечение следующее:
.
Так как 
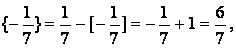имеем новое,4-е уравнение
.
Введя неотрицательную балансовую переменную 
, получим сечение 4-го дополнительного уравнения для задачи :
После выполнения I итерации имеем опорное решение 
которое одновременно и оптимальное и целочисленное. Таким образом, 
, 
.
Решение задачи :
| Номер итерации | Базисные переменные |
|
|
|
|
|
| 
|
| 
|
|
| - | |||||||||
|
| 32/7 | 1/7 | -1/7 | - | ||||||
|
| 11/7 | 1/7 | -22/7 | - | ||||||
|
| 4/7 | 1/7 | 6/7 | -1 | 2/3 | |||||
| F | ||||||||||
| I |
| |||||||||
|
| -1 | |||||||||
|
| -4 | |||||||||
|
| -7 | |||||||||
| F |
Дадим геометрическую интерпретацию решения задачи. На рис. 13.2 построена область допустимых решений задачи и показано определение ее оптимального решения. При решении задачи введено первое сечение Гомори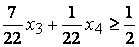 
. Исключив из него переменные и с помощью исходных уравнений, получим 
. Этому неравенству соответствует граничная прямая 
, отсекающая из области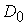 
найденное нецелочисленное решение 
, но сохраняющая все целочисленные решения.
Для новой области 
находим оптимальное решение задачи 
; при переходе к задаче строим второе сечение 
, которое после исключения базисных переменных и примет вид 
. В новой области оптимальное решение оказывается искомым целочисленным.
При определенных условиях удается доказать теорему о конечности первого алгоритма Гомори, которую мы приведем без доказательства.
Теорема 13.6. Пусть множество оптимальных планов задачи ограничено и выполняются следующие условия:
1) гарантирована целочисленность целевой функции 
(например, все 
– целые) и строка целевой функции учитывается при выборе строки для построения правильного отсечения:
2) справедливо по крайней мере одно из двух утверждений: либо целевая функция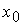 
ограничена снизу на 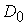, либо задача 
имеет хотя бы один план 
.
Тогда первый алгоритм Гомори требует лишь конечного числа больших итераций.
Метод Отсечений
Из вышеизложенного следует, что вид неравенства, определяющего отсечение, зависит от выбора производящей строки. Следовательно, одна и та же симплексная таблица порождает различные отсечения. Эффективность отсечения характеризуется размерами области, отсекаемой от многогранника допустимых решений. Математически это можно выразить следующим образом. Рассмотрим неравенства
(13.24)
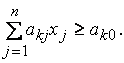(13.25)
Будем говорить, что отсечение (13.24) более эффективно, чем отсечение (13.25), если 
для всех j, причем хотя бы при одном j выполняется строгое неравенство.
Использование данного определения эффективности отсечения связано с существенными трудностями вычислительного характера. На практике отсечения обычно строят на основе производящей строки, которой соответствует 
или 
.
Оптимальное значение целевой функции (F = 63) задачи , рассмотренное в предпоследнем примере, достигается в точке 
. Поскольку значение F является целым, соответствующая строка не может быть выбрана в качестве производящей. Так как 
, первое практическое правило не позволяет осуществить выбор производящей строки. Применим второе правило. Запишем отсечения, соответствующие производящим строкам с базисными переменными и :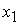
.
.
Так как
,
в качестве производящей строки следует выбрать строку с базисной переменной 
.
Оптимальное значение целевой функции 
задачи достигается в точке 
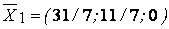. Так как 
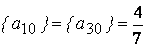, первое практическое правило не применимо. Запишем отсечения, соответствующие производящим строкам с базисными переменным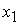и и :
;
.
Второе практическое правило также не применимо. В этом случае для образования сечения выбирается первая их данных строк.
Основные недостатки методов отсечений.
1. Ни один тип отсечений не обеспечивает высокой эффективности соответствующих вычислительных процедур.
2. Методы отсечений не подходят для решения целочисленных задач больших размерностей.
Наиболее общий вывод о возможности использования методов отсечений, по-видимому, заключается в признании того факта, что указанные методы не обеспечивают эффективного решения общей задачи целочисленного программирования.
В основе комбинаторных методов лежит идея перебора всех допустимых целочисленных решений. Наиболее известным из них является метод ветвей и границ, который также опирается на процедуру решения задачи с ослабленными ограничениями. При таком подходе из рассматриваемой задачи получаются две подзадачи путем специального разбиения пространства решений и отбрасывания областей, не содержащих допустимых целочисленных решений. В случае, когда целочисленные переменные являются булевыми, применяются комбинаторные методы. Булевы свойства переменных существенно упрощают поиск решения.
Метод ветвей и границ
Впервые метод ветвей и границ был предложен в 1960 г. А. Лэндом и А. Дойгом применительно к задаче целочисленного линейного программирования. Фактически «второе рождение» этого метода связано с работой Дж. Литтла, К. Мурти, Д. Суини и С. Кэрела. В ней же было предложено и принятое теперь название метода: «метод ветвей и границ». Он применим как к полностью, так и частично целочисленным задачам.
Приведем описание идеи данного метода. Рассматривается целочисленная (частично целочисленная) задача линейного программирования:
минимизировать
(13.26)
при условиях
(13.27)
(13.28)
(13.29)
Многогранное множество (13.27) – (13.28) предполагается ограниченным. Как в методах отсечения, процесс начинается с решения задачи линейного программирования (13.26) – (13.28). Если полученный при этом оптимальный план 
не удовлетворяет условиям целочисленности (13.29), то значение целевой функции 
на этом плане дает нижнюю границу для исходного оптимума, т.е.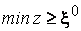 
. Пусть 
– целочисленная переменная, значение 
которой в оптимальном плане 
задачи является дробным 
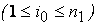. Интервал
не содержит допустимых целочисленных компонентов решения. Поэтому в оптимальном плане значение должно удовлетворять одному из неравенств: 
.
Если границы изменения заранее не заданы, то их можно вычислить, решив для этого две вспомогательные задачи линейного программирования, заключающиеся в максимизации и минимизации при условиях (13.27) – (13.28). Введение их в задачу без учета ограничения (13.29) порождает две не связанные между собой задачи. В этом случае говорят, что задача разветвляется (или разбивается) на две подзадачи. Осуществляемый в процессе ветвления учет ограничения (13.29) позволяет исключить части многогранника допустимых решений, не содержащие точки с целыми координатами. Теперь каждая подзадача решается как задача линейного программирования (с целевой функцией исходной задачи) с условиями (13.27) и дополнительным ограничением 
. Если полученный оптимум оказывается допустимым для целочисленной задачи, такое решение следует зафиксировать как наилучшее. При этом нет необходимости продолжать «ветвление» подзадачи, поскольку улучшить найденное решение, очевидно, не удастся. В противном случае подзадача вновь разбивается на две подзадачи при условии целочисленности переменных, значения которых в оптимальном решении не являются целыми. Как только полученное допустимое целочисленное решение одной из подзадач оказывается "лучше" имеющегося, оно фиксируется вместо зарегистрированного ранее. Процесс ветвления продолжается до тех пор, пока каждая подзадача не приведет к целочисленному решению или пока не будет установлена возможность улучшения имеющегося решения. Зафиксированное допустимое решение и будет оптимальным.
Эффективность вычислений можно повысить, введя в рассмотрение понятие границы, на основании которого делается вывод о необходимости дальнейшего дробления каждой из подзадач. Если оптимальное решение подзадачи без требования целочисленности обеспечивает "худшее" значение целевой функции по сравнению с имеющимся, эту подзадачу далее рассматривать не следует.
Вышеизложенное можно представить в виде некоторого дерева задач, в котором вершина 
отвечает исходному плану , а каждая из соединенных с ней ветвью вершина отвечает оптимальному плану задачи (13.26) – (13.28) при дополнительном условии . Каждой из вершин приписывается граница 
, равная минимальному (максимальному – в случае максимизации) значению z для соответствующей задачи. Ясно, что 
для всех k.
Опишем формально данный алгоритм.
1. Задание множества 
. Множество 
задается условиями (13.27) – (13.29).
2. Задание множества 
. Множество (
определяется условиями (13.27) – (13.28) и дополнительным условием
(j = 1, 2,…, n). (13.37)
3. Вычисление границ (оценок). Для множества оценка 
, где 
– оптимальный план задачи линейного программирования (13.26) – (13.28). Для множества оценка 
, где 
– оптимальный план задачи линейного программирования (13.26), (13.27), (13.30). Если множество оказывается пустым, то полагаем 
(
– в случае максимизации).
4. Вычисление планов. Если удовлетворяет условию целочисленности (13.29), то – оптимальный план задачи (13.26) – (13.29). Если удовлетворяет условию целочисленности (13.29), то – оптимальный план задачи (13.26), (13.27), (13.29), (13.30) и исходной задачи (13.27) – (13.29).
5. Ветвление. Оно необходимо в том случае, когда план 
не удовлетворяет условию целочисленности (13.29). Пусть 
– один из нецелочисленных компонентов этого плана 
. Тогда множество 
разбивается на два множества: 
, где
.
Замечание 1. Если все коэффициенты в соотношении (13.26) нецелые при 
и равны нулю при 
, то оценку 
можно заменить более сильной:
где ] a [ – наименьшее целое число, не меньшее чем а.
Замечание 2. Вопрос о наилучшем способе выбора переменной ветвления или последовательности решения конкретных задач в настоящее время не решен.
Пример. Максимизировать
(13.31)
при условиях
(13.32)
– целые. (13.33)
0-й шаг. Оптимальный план задачи (13.31) – (13.33) следующий: 
. Имеем 
. План не удовлетворяет условию целочисленности (13.33). Возьмем его не целочисленный компонент 
и разобьем на два множества:
, где
, 
.
1-й шаг. Решим две ЗЛП, состоящие из в максимизации функции (13.31) по 
и 
.
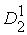Решение задачи 
:
| Номер итерации | Базисные переменные |
| 
|
|
|
| 
|
|
|
| -1 | |||||||
|
| ||||||||
|
| - | |||||||
| F | -7 | -9 | ||||||
| I |
| -1/3 | 1/3 | - | ||||
|
| 22/3 | -1/3 | 9/2 | |||||
|
| ||||||||
| F | -10 |
| II |
| 10/3 | ||||||
|
| 11/3 | |||||||
|
| ||||||||
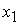
| F |
Максимум достигается при 
.
Решение задачи 
:
| Номер итерации | Базисные переменные |
|
|
|
|
|
|
|
|
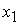
| -1 | - | ||||||
|
| ||||||||
|
| -1 | |||||||
| F | -7 | -9 | ||||||
| I |
| -1 | 11/3 | |||||
|
| ||||||||
|
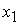
| -1 | - | ||||||
| F | -9 | |||||||
| II |
| -3 | -10 | |||||
|
| ||||||||
|
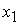
| -1 | |||||||
| F |
Максимум достигается при 
, 
и 
.
Производим разветвление по :
,
где 
, 
.
Переобозначения: 
.
2-й шаг. Решаем две задачи линейного программирования, заключающиеся в максимизации функции (13.31) по множествам 
.
Решение задачи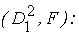 
| Номер итерации | Базисные переменные |
| 
|
|
|
|
|
|
|
| -1 | – | ||||||
|
| ||||||||
|
| – | |||||||
| F | -7 | -9 | ||||||
| I |
| 22/7 | 1/7 | 7/2 | ||||
|
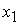
| 1/7 | 1/7 | ||||||
|
| ||||||||
| F | -8 | |||||||
| II |
| 11/7 | ||||||
|
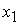
| 32/7 | |||||||
|
| &nb
Поиск по сайту©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-08-20 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |