В контрольной работе № 2 все задачи составлены из двух разделов «Введение в математический анализ» и «Производная функции». Решению примеров по математическому анализу предшествует очень большая теоретическая часть, без которой решение не возможно. С ней можно ознакомиться в учебном пособии «Высшая математика в задачах» ч.- I (Агафонова В.Н., Курган, КГУ, 2006 г., стр. 186-270.). Изучить все теоремы о бесконечно больших и бесконечно малых функциях, основные теоремы о пределах, правила предельного перехода и все неопределенные случаи, которые могут быть и как они раскрываются.
1. При вычислении предела от дроби, в числителе и знаменателе, которой содержатся бесконечно большие многочлены целых или дробных степеней встречаемся с неопределенностью  . Она раскрывается делением числителя и знаменателя дроби на наивысшую степень переменной, входящей в ее числитель или знаменатель. При этом может быть три случая:
. Она раскрывается делением числителя и знаменателя дроби на наивысшую степень переменной, входящей в ее числитель или знаменатель. При этом может быть три случая:

Отсюда можно сделать следующие выводы:
а) если степени в числители и знаменатели дроби, то предел всегда конечный,  и равен отношению коэффициентов при старших степенях переменных числителя и знаменателя;
и равен отношению коэффициентов при старших степенях переменных числителя и знаменателя;
б) если в числители степень меньше,  чем в знаменателе, предел всегда равен 0;
чем в знаменателе, предел всегда равен 0;
в) если в числителе степень больше чем в знаменателе  , то конечного предела нет, дробь будет бесконечно большой и предел ее равен
, то конечного предела нет, дробь будет бесконечно большой и предел ее равен  .
.
Замечание 1.
Если в числители или в знаменателе имеется несколько слагаемых с одинаковой наивысшей степенью, то коэффициенты при старших степенях суммируются.
Примеры:
1) 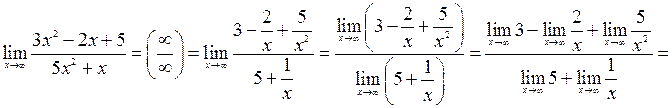

Пояснения. Разделим числитель и знаменатель на  . Применим теорему о пределе частного, т.е. вычислим предел в числителе и предел в знаменателе, затем применим теорему о пределе алгебраической суммы. Учитывая, что предел постоянной равен самой постоянной, а остальные слагаемые в числителе и знаменателе являются бесконечно малыми пределы которых равны 0, переходим к пределу и получаем ответ.
. Применим теорему о пределе частного, т.е. вычислим предел в числителе и предел в знаменателе, затем применим теорему о пределе алгебраической суммы. Учитывая, что предел постоянной равен самой постоянной, а остальные слагаемые в числителе и знаменателе являются бесконечно малыми пределы которых равны 0, переходим к пределу и получаем ответ.
2) 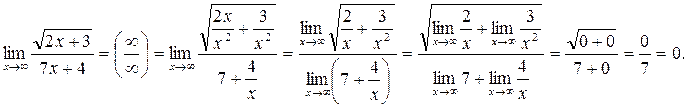
Следующая неопределенность  , которая раскрывается несколькими способами: разложением числителя и знаменателя на множители, освобождением от иррациональности, с помощью первого замечательного предела
, которая раскрывается несколькими способами: разложением числителя и знаменателя на множители, освобождением от иррациональности, с помощью первого замечательного предела  , с помощью эквивалентных абсолютно малых.
, с помощью эквивалентных абсолютно малых.
3)

Пояснения. Разлагаем на множители числитель и знаменатель дроби. В знаменатели сумму кубов разлагаем по формуле: 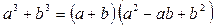 . В числителе квадратный трехчлен разлагаем на множители, решая квадратное уравнение
. В числителе квадратный трехчлен разлагаем на множители, решая квадратное уравнение  . Корни находим по теореме Виета:
. Корни находим по теореме Виета: 

Данная дробь существует в точке  , поэтому подставляем вместо
, поэтому подставляем вместо 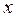 предельное значение.
предельное значение.
4) 
 .
.
Для раскрытия неопределенности домножаем числитель и знаменатель дроби на выражение, сопряженное числителю.
5)

Числитель дроби свертываем по формуле:
 .
.
Далее пользуемся эквивалентными бесконечно малыми  ;
;  .
.
6)

В числители дроби разность логарифмов заменяем логарифмом дроби (потенцируем). Затем пользуемся эквивалентными бесконечно малыми:  .
.
При раскрытии неопределенности  применяем второй замечательный предел:
применяем второй замечательный предел:
 ,
,
 .
.
Если нет этой неопределенности, то второй замечательный предел не работает. Особенность этого предела состоит в том, что второе слагаемое в скобках и показатель степени обратны по величине и одинаковы по знаку, первое слагаемое в скобках равно 1.
7)


Пояснения. В основании степени прибавляем и вычитаем 1. Затем приводим к общему знаменателю дробь и вычитаемую единицу. Затем подбираем показатель степени, обращенной второй дроби, но, чтобы не изменилось значение данного выражения, в показателе умножаем на дробь 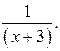 Так как возводить в степень можно при любом порядке сомножителей, стоящих в показателе степени, то расставляем скобки, указывающие этот порядок. Затем пользуемся правилом предельного перехода:
Так как возводить в степень можно при любом порядке сомножителей, стоящих в показателе степени, то расставляем скобки, указывающие этот порядок. Затем пользуемся правилом предельного перехода:

Этим правилом можно пользоваться только в том случае, если пределы в основании степени и в показатели оба конечны и одновременно не равны 0, т.е. если  и
и  .
.  и
и  одновременно не равно 0.
одновременно не равно 0.
8)


2. Непрерывность функции, точки разрыва, их классификация.
Определение. Функция  называется непрерывной в точки
называется непрерывной в точки  , если в этой точке для нее справедливо равенство
, если в этой точке для нее справедливо равенство  . В этом определении содержатся три условия, которым должна удовлетворять непрерывная функция:
. В этом определении содержатся три условия, которым должна удовлетворять непрерывная функция:
а) функция в точке  должна быть определена;
должна быть определена;
б) функция в точке  должна иметь конечный предел;
должна иметь конечный предел;
в) этот предел должен совпадать со значением функции в точке  .
.
Если нарушено хотя бы одно из трех перечисленных условий, функция в точке  будет разрывна. Разрыв может быть трех видов: разрыв I рода, II рода и разрыв III рода – «устранимый разрыв».
будет разрывна. Разрыв может быть трех видов: разрыв I рода, II рода и разрыв III рода – «устранимый разрыв».
1. Разрыв I рода в точке  будет в том случае, если функция не определена в точке
будет в том случае, если функция не определена в точке  , но имеет конечные, различные, односторонние пределы, т.е.
, но имеет конечные, различные, односторонние пределы, т.е.  ,
,
 ,
, 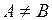 . (рисунок 1а).
. (рисунок 1а).
2. Разрыв III рода, так называемый «устранимый» разрыв, будет в том случае, если функция в точке не определена, но имеет одинаковые конечные односторонние пределы, т.е.  . (рисунок 1б).
. (рисунок 1б).
3. Все точки разрыва, не относящиеся к точкам разрыва I и III рода, являются точками разрыва II рода. В этом случае оба односторонние пределы могут быть бесконечными или один из них конечный, а другой бесконечный или не существует. (рисунок 1в, 1г).
(Графики)
Пример. Задана функция 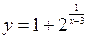 и два значения аргумента
и два значения аргумента  и
и  . Требуется:
. Требуется:
1) Установить, является ли данная функция непрерывной или неразрывной для каждого из данных значений аргумента;
2) В случае разрыва определить, какого он рода;
3) Все рассуждения обосновать.
Решение:
Исследуем точку 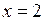 .
.
1. Функция в точке 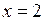 определена
определена 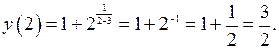
2. Вычислим предел функции в точке 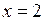 .
. 
Функция в точке 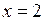 определена, поэтому при вычислении предела подставляем предельные значения аргумента
определена, поэтому при вычислении предела подставляем предельные значения аргумента 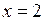 . Предел в точке
. Предел в точке 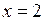 существует конечный, равный
существует конечный, равный  .
.
3. 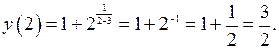
Значение функции в точке 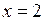 совпадает со значением предела
совпадает со значением предела 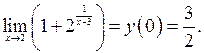
Все три условия непрерывности выполнены, значит, в точке 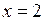 функция непрерывна.
функция непрерывна.
Исследуем точку  .
.
В этой точке функция неопределенна, т.е. не существует (показатель степени является дробью, которая не существует, так как знаменатель ее равен нулю в точке  ).
).
Нарушено первое условие непрерывности, поэтому в точке  функция терпит разрыв, исследуем на характер разрыва. Находим односторонние пределы функции в точке
функция терпит разрыв, исследуем на характер разрыва. Находим односторонние пределы функции в точке  .
.

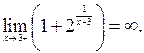
Предел справа является бесконечным, поэтому функция в точке  имеет разрыв II рода.
имеет разрыв II рода.
(График – рисунок 2)
3. Производная функции и ее приложения.
Изучить теорию по данной теме, без которой невозможно решать предлагаемые задачи с понятием производной, с основными теоремами и правилами дифференцирования, с понятием дифференциала, кроме литературы, указанной в методичке, можно ознакомиться в методических указаниях «основы дифференциального исчисления функции одной переменной» (авторы Вержбалович Т.А., Самойлова Л.В. Курган, КГУ, 2010 г.).
3.1 Основные теоремы о производных.
Если  и
и  дифференцируемые в точке
дифференцируемые в точке 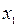 имеют место равенства:
имеют место равенства:
1)  (3.1)
(3.1)
2)  (3.2)
(3.2)
3)  (3.3)
(3.3)
4)  (3.4)
(3.4)
3.2 Производная сложной функции  и
и  , тогда
, тогда  , т.е. функция
, т.е. функция 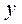 в конечном итоге зависит от
в конечном итоге зависит от  , а
, а  - это промежуточная переменная. Если функция
- это промежуточная переменная. Если функция  имеет производную в точке
имеет производную в точке  , а функция
, а функция  имеет производную в точке
имеет производную в точке  . Если существуют производные
. Если существуют производные 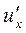 и
и  , тогда справедливо равенство:
, тогда справедливо равенство:  ,
,
т.е. производная сложной функции равна произведению производной функции по промежуточной переменной на производную промежуточной переменной по независимой. Так как производная сложной функции встречается чаще, то таблицу производных элементарных функций лучше сразу запоминать для сложного аргумента.
3.3 Таблица производных основных элементарных функций.
1)  ;
;
2)  ;
;
3) 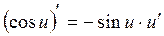 ;
;
4)  ;
;
5)  ;
;
6)  ;
;
7) 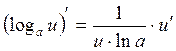 ;
;
8)  ;
;
9)  ;
;
10)  ;
;
11)  ;
;
12)  ;
;
13)  ;
;
14)  ;
;
15)  ;
;
16) 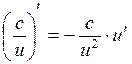 .
.
Очень часто встречаются производные от квадратичного корня и производная от дроби с постоянным числителем, поэтому удобно в этих случаях пользоваться формулами (15), (16).
Найти производные функций:
Пример 1.
 Это степенная функция со сложным основанием. Находим производную по формуле (1), затем по формуле (2).
Это степенная функция со сложным основанием. Находим производную по формуле (1), затем по формуле (2). 
Пример 2.
 . Так как функция логарифмическая со сложным аргументом, то применяем формулу (6).
. Так как функция логарифмическая со сложным аргументом, то применяем формулу (6). 
продолжаем дифференцировать по формуле (10).

 .
.
Пример 3.
 . Находим производную от дроби по формуле (3).
. Находим производную от дроби по формуле (3). 
 .
.
Пример 4.
 . Для нахождения производной применяем метод логарифмического дифференцирования.
. Для нахождения производной применяем метод логарифмического дифференцирования.
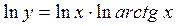 .
. 
После логарифмирования дифференцируем обе части по  .
.  .
.  Пояснения. Дифференцируем левую часть равенства по правилу дифференцирования сложной функции, т.к.
Пояснения. Дифференцируем левую часть равенства по правилу дифференцирования сложной функции, т.к.  зависит от
зависит от  .
.  (сначала по
(сначала по  , затем умножаем на производную
, затем умножаем на производную  по
по  , т.е.
, т.е.  . Правую часть дифференцируем как произведение. Затем из полученного равенства находим
. Правую часть дифференцируем как произведение. Затем из полученного равенства находим  .В ответ
.В ответ  подставляем из условия задачи. Логарифмическое дифференцирование применяется для функций
подставляем из условия задачи. Логарифмическое дифференцирование применяется для функций  .
.
Пример 5.
 . Это неявная функция, т.к.
. Это неявная функция, т.к.  не выражен через
не выражен через  . Дифференцируем по тем же формулам, что и явную, только производную от
. Дифференцируем по тем же формулам, что и явную, только производную от  находим по правилу дифференцирования сложной функции.
находим по правилу дифференцирования сложной функции.
 .
.
 .
.
Слагаемые с  переносим в одну сторону, без
переносим в одну сторону, без  - в другую. Группируем
- в другую. Группируем  и находим из полученного равенства.
и находим из полученного равенства.
 .
.  .
.
3.4 Производная от функций, заданных параметрически.
Если  и
и  являются функциями, зависящими от одного параметра
являются функциями, зависящими от одного параметра  , то это задание называется параметрическим:
, то это задание называется параметрическим:


Производная от таких функций  находится по формуле:
находится по формуле:
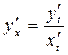 . (3.5)
. (3.5)
Пример 6.
Найти производную от функции, заданной параметрически: 



Если производную первого порядка продолжать дифференцировать дальше, то получим производную второго порядка  .
.
Пример 7.
Найти  .
. 

 .
.
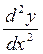 вычисляем по формуле (3.6)
вычисляем по формуле (3.6)
 .
.
3.5 Приложения производной. Геометрический смысл производной.
Численное значение производной в точке 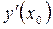 равно угловому коэффициенту касательной, проведенной в точке
равно угловому коэффициенту касательной, проведенной в точке  к графику функции
к графику функции  с положительным направлением оси
с положительным направлением оси  .
.  . Это используется для составления уравнения касательной. Оно имеет вид:
. Это используется для составления уравнения касательной. Оно имеет вид:
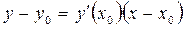 (3.7)
(3.7)
Пример 8. Составить уравнение касательной к кривой  в точке с абсциссой
в точке с абсциссой  .
.
Решение:
Находим ординату точку касания:  . Подставляем координату
. Подставляем координату  в уравнение кривой. Точка касания
в уравнение кривой. Точка касания  . Находим
. Находим  .
.
Находим угловой коэффициент касательной  . Подставляем
. Подставляем  и
и  в уравнение (3.7)
в уравнение (3.7)


 - это уравнение касательной.
- это уравнение касательной.
3. Применение производных к вычислению пределов. Правило Лопиталя.
Пусть функции  и
и  дифференцируемы в окрестности точки
дифференцируемы в окрестности точки  и
и  . Если
. Если  или
или  , т.е. частные
, т.е. частные
в точке 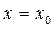 представляет собой неопределенность вида
представляет собой неопределенность вида  или
или  , то если существует предел отношения производных функций
, то если существует предел отношения производных функций  , то существует
, то существует
предел отношения самих функций и они между собой равны, т.е.
 (3.8)
(3.8)
Если частное  в точке
в точке 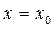 также есть неопределенность
также есть неопределенность  или
или  и производные
и производные  и
и  удовлетворяют соответствующим условиям, то можно перейти к отношению вторых производных и т.д. Если имеются неопределенности
удовлетворяют соответствующим условиям, то можно перейти к отношению вторых производных и т.д. Если имеются неопределенности 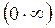 или
или  , то их следует с помощью эквивалентных преобразований привести к неопределенности
, то их следует с помощью эквивалентных преобразований привести к неопределенности  или
или  и затем применить правило Лопиталя. В случае неопределенности вида
и затем применить правило Лопиталя. В случае неопределенности вида  ,
, 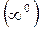 или
или 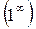 следует прологарифмировать функцию, определяющую этот предел и найти предел ее логарифма.
следует прологарифмировать функцию, определяющую этот предел и найти предел ее логарифма.
Вычислить пределы, применяя правило Лопиталя.
Пример 9.
 .
.
Пример 10. 
 .
.
Пример 11.
 Пример 12.
Пример 12.
 .
.
Обозначим вычисленный предел за  и прологарифмируем данное равенство.
и прологарифмируем данное равенство.

 Символы
Символы  и
и  поменяем местами на основе свойств непрерывности функции.
поменяем местами на основе свойств непрерывности функции.


Путем эквивалентных преобразований пришли к равенству  т.е.
т.е.  . Решая простейшее логарифмическое уравнение получим
. Решая простейшее логарифмическое уравнение получим 
- это вычисляемый предел.
Контрольная работа № 1
Элементы линейной алгебры и аналитической геометрии.
Векторная алгебра.
1-10 Даны векторы  = { a 1; a 2; a 3};
= { a 1; a 2; a 3};  = {b1; b2; b3};
= {b1; b2; b3};  ={c1; c2; c3};
={c1; c2; c3};  ={d1; d2; d3} в некотором базисе. Показать, что векторы
={d1; d2; d3} в некотором базисе. Показать, что векторы  ,
,  ,
,  образуют базис, и найти координаты вектора
образуют базис, и найти координаты вектора  в этом базисе.
в этом базисе.
1.  ={1;2;3};
={1;2;3};  ={-1;3;2};
={-1;3;2};  ={7;-3;5};
={7;-3;5};  ={6;10;17}.
={6;10;17}.
2.  ={4;7;8};
={4;7;8};  ={9;1;3};
={9;1;3};  ={2;-4;1};
={2;-4;1};  ={1;-13;-13}.
={1;-13;-13}.
3.  ={8;2;3};
={8;2;3};  ={4;6;10};
={4;6;10};  ={3;-2;1};
={3;-2;1};  ={7;4;11}.
={7;4;11}.
4.  ={10;3;1};
={10;3;1};  ={1;4;2};
={1;4;2};  ={3;9;2};
={3;9;2};  ={19;30;7}.
={19;30;7}.
5.  ={2;4;1};
={2;4;1};  ={1;3;6};
={1;3;6};  ={5;3;1};
={5;3;1};  ={24;20;6}.
={24;20;6}.
6.  ={1;7;3};
={1;7;3};  ={3;4;2};
={3;4;2};  ={4;8;5};
={4;8;5};  ={7;32;14}.
={7;32;14}.
7.  ={1;-2;3};
={1;-2;3};  ={4;7;2};
={4;7;2};  ={6;4;2};
={6;4;2};  ={14;18;6}.
={14;18;6}.
8.  ={1;4;3};
={1;4;3};  ={6;8;5};
={6;8;5};  ={3;1;4};
={3;1;4};  ={21;18;33}.
={21;18;33}.
9.  ={2;7;3};
={2;7;3};  ={3;1;8};
={3;1;8};  ={2;-7;4};
={2;-7;4};  ={16;14;27}.
={16;14;27}.
10.  ={7;2;1};
={7;2;1};  ={4;3;5};
={4;3;5};  ={3;4;-2};
={3;4;-2};  ={2;-5;-13 }.
={2;-5;-13 }.
11-20 Даны координаты вершин пирамиды А1А2А3А4. Средствами векторной алгебры и аналитической геометрии найти:
1) длину ребра А1А2;
2) угол между ребрами А1А2 и А1А4;
3) площадь грани А1А2А3;
4) объем пирамиды;
5) уравнение прямой А1А2;
6) уравнение плоскости А1А2А3;
7) уравнение высоты, опущенной из вершины А4 на грань А1А2А3.
11. А1(4;2;5), А2(0;7;2), A3(0;2;7), A4(1;5;0).
12. A1(4; 4; 10), A2(4;10;2), A3(2;8;4), A4(9;6;4).
13. A1(4;6;5), A2(6;9;4), A3(2;10;10;), A4(7;5;9).
14. A1(3;5;4), A2(8;7;4), A3(5;10;4), A4(4;7;8).
15. A1(10;6;6), A2(-2;8;2), A3(6;8;9), A4(7;10;3).
16. A1(1;8;2), A2(5;2;6), A3(5;7;4), A4(4;10;9).
17. A1(6;6;5), A2(4;9;5), A3(4;6;11), A4(6;9;3).
18. A1(7;2;2), A2(5;7;7), A3(5;3;1), A4(2;3;7).
19. A1(8;6;4),A2(10;5;5), A3(5;6;8), A4(8;10;7).
20. A1(7;7;3), A2(6;5;8), A3(3;5;8), A4(8;4;1).
21-30 Найти точку М1, симметричную точке М относительно плоскости.
21. М (-1; 0; -1), 2x + 6y – 2z + 11 = 0.
22. М (0; 2; 1), 2x + 4y – 3 = 0.
23. М (2; 1; 0), y + z + 2 = 0.
24. М (-1; 2; 0), 4x – 5y – z – 7 = 0.
25. М (2; -1; 1), x – y + 2z – 2 = 0.
26. М (1; 1; 1), x + 4y + 3z + 5 = 0.
27. М (1; 2; 3), 2x + 10y + 10z – 1 = 0.
28. М (1; 0; -1), 2y + 4z – 1 = 0.
29. М (3; -3; -1), 2x – 4y – 4z – 13 = 0.
30. М (-2; -3; 0), x + 5y + 4 = 0.
31-40 Дана система линейных уравнений. Доказать ее совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.
31.  32.
32. 
33.  34.
34. 
35.  36.
36. 
37.  38.
38. 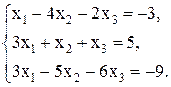
39.  40.
40. 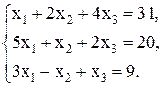
Контрольная работа №2