Экспоненциальным (или показательным) называется непрерывное распределение вероятностей, плотность которого определяется по формуле:
, (3.19)
для х >0 и f (x)=0 для x <0, а число l называется параметром экспоненциального распределения. По формуле (3.4) легко найти интегральную функцию экспоненциального распределения:
, (3.20)
для х >0 и F (x)=0 для х <0.
Для экспоненциального распределения среднее значение случайной величины равно ее стандартному отклонению и равно 1/l.
В Excel экспоненциальное распределение вычисляется функцией ЭКСПРАСП(х; l; тип), где тип ={ложь, истина}. Если указать ложь, то будет вычислена плотность экспоненциального распределения по формуле (3.19), а если указать вместо тип – истина, то будет вычислена интегральная функция (3.20).
Распределение Вейбулла.
Распределением Вейбулла называется непрерывное распределение вероятностей, плотность которого определяется формулой:
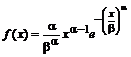, (3.21)
где a и b - параметры распределения Вейбулла. По формуле (3.4), используя (3.21), можно найти интегральную функцию распределения Вейбулла:
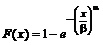. (3.22)
Если a=1 и b=1/l, то распределение Вейбулла совпадает с экспоненциальным, т.е. (3.21) совпадает с (3.19), а (3.22) – с (3.20).
В Excel распределение Вейбулла вычисляется функцией ВЕЙБУЛЛ(х; a; b; тип), где параметр тип определяет, какую функцию вычислять плотность или интегральную функцию. Если в качестве этого параметра указать ложь, то будет вычислена плотность (3.21), а если – истина, то интегральная функция (3.22).
Гамма-распределение.
Гамма-распределением (g-распределением) называется распределение непрерывной случайной величины, плотность которого определяется формулой:
, (3.23)
где a, b - параметры g-распределения, 
- гамма-функция Эйлера.
Если b=1, то g-распределение называется стандартным. Если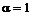 
и b=1/l, то плотность g-распределения (3.23) совпадает с экспоненциальным (3.19).
Если a= k /2, где k - целое положительное число, 
, то g-распределение (3.23) совпадает с распределением Пирсона (3.13) с k степенями свободы.
В Excel g-распределение вычисляется функцией ГАММАРАСП(х; х; a; b; тип), где параметр тип такой же, как и для предыдущих функций: если тип =истина, то вычисляется интегральная функция g-распределения, а если тип =ложь, то вычисляется плотность (3.23).
В Excel можно вычислить обратную и интегральную функции g-распределения функции ГАММАОБР(p;a; b), где p - вероятность, для которой следует найти аргумент х интегральной функции g-распределения.
В формулу (3.23) входит гамма-функция Эйлера, определяемая равенством:
. (3.24)
В Excel имеется функция ГАММАНЛОГ(a), вычисляющая ln(G(a)). С помощью этой функции можно вычислить непосредственно гамма-функцию (3.24) по формуле: =EXP(ГАММАНЛОГ(a)).
Практические задания
3.1. Графики функции нормального распределения
Построить на одном рисунке графики функции нормального распределения для s=3 и различных значений а: -2; 0; 2; 5. На другом рисунке построить графики функции нормального распределения для а =2 и различных значений s: 1; 3; 4,6.
Для выполнения этого задания проделайте следующие пункты.
1. Сначала постройте графики F (x) нормального распределения для фиксированного s и различных а. Это позволит увидеть изменение формы кривой с изменением среднего значения.
2. В ячейку А1 наберите: -10. Выделите эту ячейку и выполните команду Правка ® Заполнить ® Прогрессия.
3. В появившемся диалоговом окне Прогрессия установите:
· в поле Шаг: 0,5;
· в поле Предельное значение: 10;
· в группе Расположение активизируйте переключатель по столбцам и нажмите ОК.
В результате интервал ячеек А1:А41 будет заполнен числами от –10 до 10 с шагом 0,5. Эти числа будут значениями переменной х, для которой будем вычислять F (x).
4. В ячейку В1 поместите значение функции нормального распределения для числа, содержащегося в А1, и а =-2, s=3. Для этого в В1 следует набрать формулу: =НОРМРАСП(А1; -2; 3; истина). Далее в ячейку С1 наберите формулу: =НОРМРАСП(А1; 0; 3; истина); в ячейку D1 – формулу: =НОРМРАСП(А1; 2; 3; истина); в ячейку Е1 - формулу: =НОРМРАСП(А1; 5; 3; истина).
5. Заполнить все ячейки этими формулами по столбцам проще всего с помощью таблицы подстановки. Для этого выделите диапазон А1:Е41 и выполните команду Данные ® Таблица подстановки. В появившемся диалоговом окне Таблица подстановки поместите курсор в поле Подставлять значения по строкам в, а затем щелкните мышью по ячейке А1 и нажмите ОК. В результате получится таблица, содержащая для каждого х значение F (x) при s=3 и а =-2 (в столбце В); а =0 (в столбце С); а =2 (в столбце D) и а =5 (в столбце Е).
6. Сразу, не снимая выделения с таблицами, вызовите Мастер диаграмм и выберите в нем Тип: Точечная и Вид: точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров и нажмите Готово.
7. Самостоятельно отредактируйте полученную диаграмму и приведите ее к следующему виду:
Из этого рисунка видно, что с увеличением среднего значения а и фиксированном стандартном отклонении s кривая интегральной функции распределения перемещается параллельным переносом слева направо (без деформации формы).
8. Теперь постройте графики интегральной функции распределения для фиксированного а =0 и различных s, указанных в задании.
9. Перейдите на другой рабочий лист и с помощью автозаполнения, точно также, как и в п.2-3, заполните столбец А значениями х.
10. В ячейку В1 наберите формулу: =НОРМРАСП(А1; 0; 1,5; истина); в С1 - формулу: =НОРМРАСП(А1; 0; 3; истина); в D1 – формулу: =НОРМРАСП(А1; 0; 4,5; истина).
11. Повторите процедуру п.5-6 для использования таблиц подстановки и построение диаграммы.
12. Полученную диаграмму приведите к виду:
Из этого рисунка видно, что кривая интегральной функции распределения при фиксированном среднем значении а и с увеличением стандартного отклонения s деформируется, растягиваясь симметрично относительно центральной точки с координатами (0; 0,5).
3.2. Графики биномиального распределения
Построить на одном рисунке графики биномиального распределения (3.8) для фиксированной вероятности р =0,2 и различных значений числа испытаний n: 5; 10; 20; 50. На другом рисунке построить графики этой же функции для фиксированного числа испытаний n =20 и различных значений вероятности р: 0,1; 0,25; 0,5; 0,75; 0,9.
Для выполнения этого задания проделайте следующие пункты.
1. Перейдите на следующий рабочий лист.
2. В ячейку А1 наберите число 0, и заполните ячейки ниже целыми числами до 20 с помощью автозаполнения. Тогда в интервале ячеек А1:А21 будут содержаться значения m, для которых будет вычисляться вероятность по формуле Бернулли (3.8).
3. В ячейку В1 наберите формулу: =БИНОМРАСП(А1; 5; 0,2; ложь); в С1 – формулу: =БИНОМРАСП(А1; 10; 0,2; ложь); в D1 - формулу: =БИНОМРАСП(А1; 20; 0,2; ложь); в Е1 - формулу: =БИНОМРАСП(А1; 50; 0,2; ложь).
4. Теперь с помощью Таблиц подстановки по процедуре, описанной в задании 3.1 п.5 создайте таблицу значений распределения Бернулли. Полученная после этого таблица должна занимать диапазон А1:Е21 и содержать значения вероятностей, вычисленных по формуле Бернулли для р =0,2 и различных чисел испытаний n: 5; 10; 20 и 50, соответственно.
5. Не сбрасывая выделения с этой таблицы, вызовите Мастер диаграмм и выберите: Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров и нажмите Готово.
6. Самостоятельно приведите полученную диаграмму к следующему виду:
Из этого рисунка видно, что при фиксированной вероятности наступления события А с увеличением числа независимых испытаний n кривые «расплываются»: максимумы уменьшаются, смещаясь вправо. Это означает, что с увеличением числа испытаний n, наивероятнейшее число появлений события А (т.е. такое число m, для которого вероятность 
максимальная) смещается в сторону больших значений.
7. Теперь постройте аналогичным образом графики функции по формуле Бернулли (3.8) для фиксированного числа независимых испытаний n =20 и различных вероятностей р, указанных в условии задания.
8. Перейдите на следующий рабочий лист и заполните столбец А точно также, как и в п.2 этого здания.
9. В ячейку В1 наберите формулу: =БИНОМРАСП(А1; 20; 0,1; ложь); в ячейку С1 – формулу: =БИНОМРАСП(А1; 20; 0,25; ложь); в D1 - формулу: =БИНОМРАСП(А1; 20; 0,5; ложь); в Е1 - формулу: =БИНОМРАСП(А1; 20; 0,75; ложь); в F1 - формулу: =БИНОМРАСП(А1; 20; 0,9; ложь).
10. С помощью Таблицы подстановки заполните этими формулами все ячейки ниже до 21-й строки. Тогда диапазон А1:F21 будет содержать значения вероятностей, вычисленных по формуле Бернулли для n =20 и p =0,1 (в столбце В); p =0,25 (в столбце С); p =0,5 (в столбце D); p =0,75 (в столбце Е); и p =0,9 (в столбце F).
11. Повторив действия п.5 этого задания, постройте графики биномиального распределения по полученной таблице и приведите его к виду:
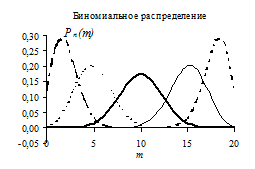
Из этого рисунка видно, что распределение Бернулли для фиксированного числа испытаний n симметрично относительно изменения вероятности p, причем, при p =0,5 наивероятнейшее число есть m = n /2.
3.3. Графики распределения Пуассона
Построить на одном рисунке графики распределения Пуассона (3.10) для различных значений параметра l: 0,1; 0,5; 1; 2; 5; 10.
Для выполнения этого задания проделайте следующие пункты.
1. Перейдите на следующий рабочий лист.
2. В ячейку А1 наберите число 0, и заполните ячейки ниже целыми числами до 20 с помощью автозаполнения. Тогда в интервале ячеек А1:А21 будут содержаться значения m, для которых будет вычисляться вероятность по формуле Пуассона (3.10).
3. В ячейку В1 наберите формулу: =ПУАССОН(А1; 0,1; ложь); в С1 – формулу: =ПУАССОН (А1; 0,5; ложь); в D1 – формулу: =ПУАССОН(А1; 1; ложь); в Е1 – формулу: =ПУАССОН(А1; 2; ложь); в F1 – формулу: =ПУАССОН(А1; 5; ложь); в G1 – формулу: =ПУАССОН(А1; 10; ложь).
4. Теперь с помощью Таблиц подстановки по процедуре, описанной в задании 3.1 п.5 создайте таблицу значений распределения Пуассона. Полученная после этого таблица должна занимать диапазон А1:Е21 и содержать значения вероятностей, вычисленных по формуле Пуассона для р =0,2 и различных чисел испытаний n: 5; 10; 20 и 50, соответственно.
5. Не сбрасывая выделения с этой таблицы, вызовите Мастер диаграмм и выберите: Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров и нажмите Готово.
6. Самостоятельно приведите полученную диаграмму к следующему виду:
Из этого рисунка видно, что изменение формы кривых распределения Пуассона (3.10), с ростом параметра l похоже на динамику кривых распределения Бернулли (3.8).
3.4. Графики распределения Стьюдента
Построить на одном рисунке графики интегральной функции распределения Стьюдента для чисел степеней свободы 2; 4; 10 и стандартной функции нормального распределения. На другом рисунке построить графики плотности стандартного нормального распределения и плотности распределения Стьюдента по формуле (3.15) для чисел степеней свободы 2; 4.
Для выполнения этого задания проделайте следующие пункты.
1. Перейдите на новый рабочий лист.
2. В столбце А разместите значения переменной х от 0 до 10 через 0,5 с помощью автозаполнения, начиная с ячейки А1.
3. В ячейку В1 поместите формулу: =1-СТЬЮДРАСП(А1; 2; 1); в ячейку С1 - формулу: =1-СТЬЮДРАСП(А1; 4; 1); в ячейку D1 - формулу: =1-СТЬЮДРАСП(А1; 10; 1); в ячейку Е1 - формулу: =НОРМСТРАСП(А1).
4. С помощью Таблиц подстановки заполните диапазон А1:Е1 данными, необходимыми для построения графиков.
5. Проделывая действия, описанные в предыдущих заданиях, постройте графики на одной диаграмме и приведите ее к следующему виду:
Жирной сплошной линией на этом рисунке выделена кривая стандартного нормального распределения. Видно, что с ростом числа степеней свободы k интегральная функция распределения Стьюдента быстро стремится к интегральной функции стандартного нормального распределения (3.7).
6. Теперь постройте на одном рисунке графики плотности стандартного нормального распределения и плотности распределения Стьюдента для различных значений числа степеней свободы k, указанных в задании.
7. Перейдите на следующий рабочий лист. Заполните ячейки столбца А, начиная с А1, числами от –6 до 6 через 0,5, используя процедуру автозаполнения.
8. В какую-либо справа ячейку, например, в Н1, поместите число степеней свободы 2, а в ячейку Н2 - число степеней свободы 4.
9. В ячейку I1 поместите нормировочный множитель плотности распределения Стьюдента. Для этого наберите в эту ячейку формулу: =EXP(ГАММАНЛОГ((H1+1)/2))/(КОРЕНЬ(ПИ()*H1)*EXP(ГАММАНЛОГ(H1/2))). Затем скопируйте эту формулу в ячейку I2. В результате в ячейке I1 должно получиться число 0,35355339, а в I2 – число 0,375.
10. В ячейку В1 поместите плотность распределения Стьюдента (3.15). Для этого наберите в эту ячейку формулу: =(1+А1^2/H1)^(-(H1+1)/2)*I1, в ячейку С1 наберите формулу: =(1+A1^2/H2)^(-(H2+1)/2)*I2.
11. В ячейку D1 поместите стандартную плотность нормального распределения (3.5). Для этого в D1 наберите формулу: =НОРМРАСП(А1; 0; 1; ложь).
12. Выделите диапазон ячеек А1:D25 и с помощью Таблиц подстановки заполните его значениями набранных функций. Затем вызовите Мастер диаграмм и постройте графики. Полученную диаграмму приведите к виду:
Жирной сплошной линией выделена кривая плотности стандартного нормального распределения (3.5). Видно, что с ростом k к этой линии стремятся кривые плотности распределения Стьюдента (3.15).