Глава 6
ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКИХ МЕТОДОВ
ПРИ РАСЧЁТАХ РАЗРАБОТКИ
В практических задачах моделирования процессов разработки нефтяных и газовых месторождений получение точных и даже приближённых решений оказывается весьма затруднительным, а в ряде случаев и невозможным. Причины тому сложная конфигурация месторождений; неоднородность по площади и разрезу; тектонические нарушения геологической структуры и др. Приведённые ранее решения некоторых задач используются для качественных и количественных оценок интегральных показателей разработки при проектировании и оценки использования тех или иных систем разработки.
Модель разработки нефтяного месторождения обычно представляется математически в виде системы, состоящей из алгебраических, дифференциальных, интегральных уравнений или соотношений. Для того чтобы провести расчёт на основе уже созданной модели разработки месторождения, необходимо сначала решить соответствующие математические задачи. Только получив решение этих задач, можно осуществлять сам расчёт в цифрах. Точные оценки поведения залежи в процессе разработки осуществляется с помощью ЭВМ на основе численных методов решения задач фильтрации.
Методы получения точных решений задач
Математической физики
Многие задачи разработки нефтяных и газовых месторождений сводятся к решению классических уравнений математической физики. В ряде случаев можно получать решения задач математической физики, в точности удовлетворяющие исходным уравнениям, начальным и граничным условиям. Такие решения называются точными. К числу методов, дающих точные решения задач разработки нефтяных месторождений, относится хорошо известный из курса математики метод разделения переменных (метод Фурье), методы функций комплексного переменного, интегральных преобразований, получения автомодельных решений и др.
Методы функций комплексного переменного являются классическими методами решения задач установившейся фильтрации несжимаемой жидкости в плоских пластах. Рассмотрим эти методы при установившемся притоке жидкости к источникам (скважинам).
1. Уравнение неразрывности массы жидкости, фильтрующейся в плоском пласте, имеет, исходя из (4.12), следующий вид:
. (6.1)
Подставляя в это уравнение формулу закона Дарси
; 
(6.2)
получаем уравнение Лапласа
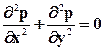. (6.3)
Введем потенциал фильтрации в виде
.
В этом случае вместо уравнения (6.3) получим
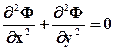. (6.4)
Введем комплексный потенциал
; 
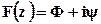. (6.5)
Входящая в выражение (6.5) функция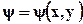 
– функция линий тока. В теории плоского потенциала доказывается, что комплексный потенциал 
и функция линий тока удовлетворяют условиям Коши – Римана
; 
. (6.6)
Таким образом, любая аналитическая функция комплексного переменного описывает некоторое плоское течение в пласте.
Рисунок 6.1 – Схема бесконечной цепочки скважин в плоском пласте: 1 – скважины; 2 – полоса шириной 2а
Допустим, что в неограниченном плоском пласте (рисунок 6.1) по оси х располагается бесконечная цепочка источников (скважин). Каждая из скважин находится на расстоянии 2s от соседней. Для того чтобы найти решение задачи о течении жидкости в пласте, достаточно рассмотреть течение жидкости только в одной полосе шириной 2а, расположенной по обе стороны от оси у.
Получить формулу притока жидкости к одному источнику можно было бы путем суммирования бесконечного числа решений для источников, расположенных на расстояниях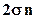 
(
) от рассматриваемого источника, находящегося в начале координат. Однако более компактно это можно сделать, применив конформное преобразование полосы, расположенной в плоскости , в неограниченную плоскость комплексного переменного 
. Такое конформное преобразование дает функция
. (6.7)
При конформном преобразовании, осуществляемом функцией (6.7), любой точке полосы 
соответствует определенная точка плоскости z.
Можно с достаточным приближением считать, что вместо точечного источника в плоскости z существует скважина радиусом rс, где потенциал равен Фс. Тогда примем, что на расстоянии rк от центра скважины потенциал равен Фк. Для дебита скважины в плоскости z можно написать формулу Дюпюи
. (6.8)
Если перейти к некоторой плоскости z, то при больших значениях у течение в полосе будет параллельным оси у. Для этой оси имеем
.
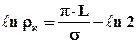При значительных расстояниях по оси у имеем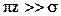 
. Тогда можно положить
.
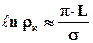При незначительных 
.
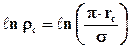Подставляя приведённые значения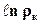 
и 
в формулу (6.8), получаем
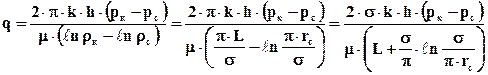. (6.9)
По формуле (6.9) можно определить дебит одной скважины из бесконечной цепочки скважин, расположенных в неограниченном пласте, при условии, что на некотором, достаточно большом расстоянии z от оси х давление равно рк, а в скважинах малого радиуса rс оно составляет рс.
2. Рассмотрим решение одной из основных задач теории теплопроводности, весьма необходимое при расчётах тепловых методов разработки нефтяных месторождений. Пусть имеем полубесконечный стержень площадью течения S, полностью теплоизолированный от окружающей среды. Начальная температура при 
во всем стержне была равна То, а при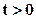 
на границе стержня 
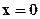(рисунок 6.2) она стала равной Т1, оставаясь при 
равной То. Требуется определить распределение температуры по координате х в различные моменты времени t.
Будем исходить из уравнения сохранения энергии, рассматривая теплоперенос в стержне только за счёт теплопроводности. Для скорости теплопереноса uт за счёт теплопроводности имеем следующее уравнение:
Рисунок 6.2 – Схема распространения температуры за счёт теплопроводности в полубесконечном стержне: 1 – полубесконечный стержень площадью сечения S; 2 – распределение температуры в стержне в момент времени t
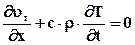, (6.10)
где с – удельная теплоемкость вещества в стержне; r – плотность вещества.
Скорость переноса тепла uт за счёт теплопроводности можно определить по формуле закона Фурье
, (6.11)
где lт – коэффициент теплопроводности.
Подставляя (6.11) в (6.10), получаем
; 
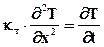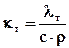. (6.12)
Уравнение (6.12) есть уравнение теплопроводности при прямолинейном распространении тепла, а входящий в него коэффициент kт называется коэффициентом температуропроводности. В соответствии с условиями задачи
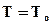при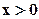 
, ; , 
,
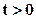(6.13)
при , .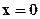
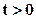Рассмотрим функцию 
, определяемую следующим образом:
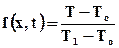. (6.14)
Тогда начальное и граничное условия (6.13) запишутся следующим образом:
при , ; , ,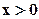
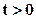(6.15)
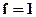при , .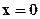
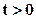Функция , очевидно, также удовлетворяет уравнению теплопроводности (6.12), как и 
, т.е.
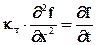. (6.16)
Для получения решения рассматриваемой задачи применим преобразование Лапласа. В результате получим выражение для скорости переноса тепла на границе 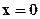. С учётом выражения (6.11) находим
;
(6.17)
.
Поток тепла qт через течение стержня площадью S при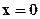
. (6.18)
3. Рассмотрим приток жидкости (нефти) с постоянным дебитом q к точечному стоку, расположенному в однородном бесконечно простирающемся плоском пласте толщиной h при упругом режиме. Сток находится в центре координат, и течение к нему в пласте радиальное. В начальный момент времени пластовое давление постоянно и составляет рк. При 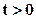из точечного стока отбирается из пласта нефть с дебитом 
, а пластовое давление остается равным рк только при 
. Требуется определить распределение давления в пласте в любой момент времени.
Уравнение неразрывности массы фильтрующегося в пласте вещества имеет в рассматриваемом случае следующий вид:
. (6.19)
Учитывая закон Дарси и сжимаемость пласта (сжимаемость пород пласта и насыщающей их жидкости), из (6.19) получаем уравнение упругого режима в следующем виде:
; 
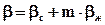, (6.20)
где bс и bж – сжимаемость соответственно пород пласта и насыщающей пласт жидкости. Остальные обозначения такие же, что и принятые выше в формуле закона Дарси. Введём функцию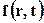 
следующим образом:
(6.21)
и подставим ее в уравнение (6.11). В результате получим
. (6.22)
Здесь k – пьезопроводность пласта. Поскольку сток точечный (
), то для него имеем следующее граничное условие:
.
Следовательно, граничное и начальное условия будут
;
(6.23)
.
Известно, что рассматриваемое решение задачи зависит от одной переменной 
. В таких случаях считают, что решение автомодельное, т.е. подобное самому себе.
Приближённые методы
Из приближённых методов расчёта в теории разработки нефтяных месторождений наиболее распространены метод эквивалентных фильтрационных сопротивлений Ю.П. Борисова и метод интегральных соотношений Г.И. Баренблатта. Первый из указанных методов используют при расчёте установившихся течений жидкостей в плоских пластах со скважинами, а второй – в расчётах перераспределения давления жидкости при упругом режиме, неустановившегося движения газа и реже – задач диффузии, теплопроводности и конвекции. Метод интегральных соотношений хорошо разработан только для решения одномерных задач.
Рассмотрим вначале метод эквивалентных фильтрационных сопротивлений. Справедливость этого метода можно показать на примере конкретного решения о притоке жидкости к бесконечной цепочке скважин. Так, перепишем формулу (6.9) следующим образом:
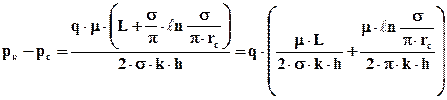. (6.24)
Первый член выражения, стоящего в скобках (6.24), характеризует фильтрационное сопротивление при движении жидкости в полосе шириной 2а на расстоянии от 0 до L, а второй член – фильтрационное сопротивление при радиальном движении жидкости от кругового контура 
до окружности радиуса rс. Борисов Ю.П. назвал фильтрационное сопротивление 
– внешним, а 
– внутренним и предположил, что и в более сложных случаях установившихся плоских фильтрационных течений фактические фильтрационные сопротивления можно разделить на эквивалентные внешние и внутренние.
Метод эквивалентных фильтрационных сопротивлений позволяет рассчитывать с достаточной для практики точностью дебиты и давления в пластах при различных системах разработки.
Рассмотрим однорядную систему разработки со схемой расположения скважин, показанной на рисунке 6.3. При этом происходит поршневое вытеснение нефти водой из пласта толщиной h. Вязкость нефти в пластовых условиях составляет mн, а вязкость воды mв. Абсолютная проницаемость пласта k, а относительные проницаемости для нефти и воды, являющиеся постоянными согласно модели поршневого вытеснения нефти водой, равны соответственно kн и kв,радиус добывающей скважины rс, радиус нагнетательной скважины rнс. Вода в процессе вытеснения нефти в момент времени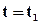 
дошла до расстояния 
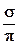от нагнетательной скважины (рисунок 6.3). При этом расстояния между добывающими и нагнетательными скважинами равны. Дебит одной добывающей скважины, равный рас-
Рисунок 6.3 – Схема распределения давления в элементе однорядной системы разработки: 1 – нагнетательные скважины; 2 – добывающие скважины; 3 – элемент однорядной системы разработки; 4 – эпюра пластового давления в сечении АА'
ходу одной нагнетательной скважины, постоянен и составляет q. Требуется определить перепад давления между нагнетательной и добывающей скважинами.
Рассмотрим течение в одном элементе пласта (рисунок 6.3, заштрихованный квадрат) шириной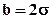 
. Обозначим давление на расстоянии от нагнетательной скважины, равном 
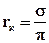, через 
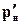. В соответствии с условием задачи и формулой Дюпюи
.
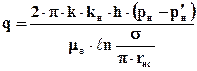Согласно методу эквивалентных фильтрационных сопротивлений течение в рассматриваемом элементе складывается из трёх: радиального (течение воды) от нагнетательной скважины радиусом rнс до контура радиусом 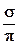, прямолинейного (течение нефти) от галереи 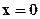, где давление 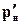, до галереи 
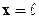, где давление 
и радиального (течение нефти) – от контура радиусом 
, где давление также равно , до добывающей скважины радиусом rс. Учитывая, что ввиду симметрии прямолинейное течение происходит с расходом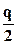 
(вправо и влево от нагнетательной скважины уходит жидкость с расходом 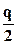), получаем
.
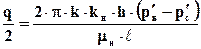Наконец, для дебита добывающей скважины имеем формулу
.
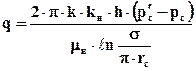Перепишем приведённые выше выражения относительно перепадов давлений в виде
; 
; 
.
Сложим эти выражения. В результате получим требующийся ответ
.
Рассмотрим ту же задачу, что и (6.12) – (6.13), но решим ее методом интегральных соотношений Г.И. Баренблатта, согласно которому приближённое решение задачи представляется в виде многочлена. Далее считаем, что приближённое распределение температуры удовлетворяет не исходному дифференциальному уравнению, а интегральным соотношениям, получаемым в результате умножения левой и правой частей уравнения на координату в степени n и их интегрирования. При использовании описываемого приближённого метода принимают, что всякое незначительное изменение температуры в случае теплопроводности или давления в случае упругого режима распространяется не мгновенно, а существует в ограниченной «возмущённой» области. Для рассматриваемой задачи интегральное соотношение имеет вид
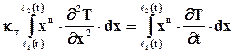, (6.25)
где n – любое, обычно целое число, начиная с нуля. Положим в качестве первого приближения 
и возьмём решение в виде
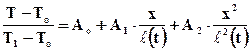. (6.26)
Выполним граничные и начальное условия, которые при приближённом решении задачи имеют несколько иной вид, чем при точном решении, а именно:
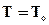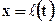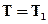при 
; 
при 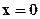. (6.27)
Должно также всегда выполняться условие 
. При решении задачи приближённым методом необходимо также дополнительно выполнять условие
. (6.28)
Соблюдая приведённые условия, получаем
; 
; 
.
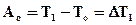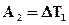Таким образом,
. (6.29)
Для определения 
подставляем (6.29) в (6.25) при , считая 
. В результате получим уравнение
.
Отсюда
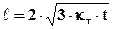, (6.30)
т.е. задача решена.
Определим, как и в примере 2, скорость уноса тепла при 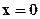. Имеем
. (6.31)
Сравнивая приведённое приближённое выражение с точным (6.18), находим, что скорость уноса тепла, определенная приближённым методом, будет больше точной в 
раз, т.е. всего примерно на 2 %.
Численные методы
Основным численным методом, используемым в разработке, является конечно-разностный метод решения дифференциальных уравнений в частных производных, для которого имеется большое количество программ для ЭВМ, разработанных в различных институтах (ВНИИ, ОАО «БашНИПИнефть», ОАО «РосНИПИтермнефть» и др.) и отечественных и зарубежных фирмах (ЮКОС, Лукойл, Shell и др.).
В современных расчётах разработки реальных нефтяных месторождений чаще всего применяют конечно-разностные методы. При использовании этих методов дифференциальные уравнения, описывающие процессы разработки нефтяных месторождений, представляют в конечно-разностной форме. Конечно-раз-ностные уравнения решают с помощью быстродействующих электронно-вычисли-тельных машин-компьютеров. Удобные для использования точные решения задач разработки нефтяных месторождений практически обычно получают только для одномерных случаев (прямолинейное и радиальное течения). При необходимости же рассчитать процессы разработки пластов с учётом их сложной геометрической формы, получить точные и даже приближённые решения не удается. В таких случаях решить задачу можно, применяя численные методы.
Хотелось бы отметить, что решение дифференциальных уравнений в частных производных можно назвать целой областью математики, которую необходимо изучать несколько лет, и поэтому полученные в этом разделе сведения носят весьма ограниченный характер. Однако он должен дать возможность ориентироваться при использовании программ для ЭВМ при численном решении задач фильтрации.
Например, пусть задана некоторая конфигурация месторождения (рассматривается двумерный случай) (рисунок 6.4). При на контуре Г известно 
и режим водонапорный. Известно распределение по всем ячейкам значений проницаемости 
и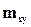 
. Вытеснение водой нефти поршневое, т.е. жидкости (нефть и вытесняющая ее вода) не смешиваются. Известны моменты времени ввода в эксплуатацию каждой k-той скважины (стока) и ее режим работы (
; 
). Предполагается, что пласт расположен на одной глубине по всей площади, имеет одинаковую мощность и изотропен в разрезе. Вязкость нефти и законтурной воды известны.
Рисунок 6.4 – Схема разбиения области со сложной конфигурацией на конечно-разностные ячейки: 1 – контур области; 2 – ячейка А
Необходимо рассчитать перераспределение давления в области со сложной конфигурацией при упругом режиме с момента пуска первой скважины до некоторого момента времени и определить продвижение границы водонефтяного контакта (ВНК).
Вот такая очень упрощенная задача, в которой не учитывается пространственная неоднородность, не учитывается смешение нефти и вытесняющей ее воды, не принимается различие пласта по мощности по площади месторождения, не учитывается качество вскрытия пластов в каждой скважине и многое другое. Современные программы для ЭВМ позволяют решать гораздо более сложные задачи.
Основой численных методов решения дифференциальных уравнений в частных производных являются:
1) дискретизация области и выбор сетки решения (плоской и пространственной);
2) замена уравнений на соответствующие разностные операторы;
3) составление системы алгебраических уравнений согласно математической постановке задачи (вид уравнения и граничные условия);
4) численное решение системы алгебраических уравнений (по шагам времени и по «молекулам»);
5) оценка устойчивости решений.
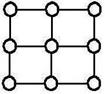
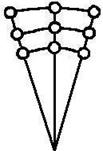
Дискретизация области подразумевает её разбиение с помощью сеток. Для плоскости сетки представляют собой
| 
| |
| прямоугольная | полярная | |
| 
| |
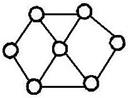
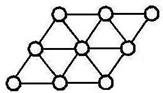
| треугольная |
Эти сетки выбираются с целью наилучшего приближения к границам или чтобы повысить точность вычисления в какой-либо интересующей области.
В зависимости от вида сетки записываются и конечно-разностные операторы (часто называют молекулы, так как их изображают в виде строгих формул), которые заменяют соответствующие дифференциальные операторы
; 
; 
; 
; 
…
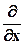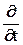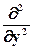Для примера будем рассматривать прямоугольную сетку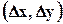 
и выпишем молекулы. Возьмем и рассмотрим одну ячейку (рисунок 6.4).
В этом двумерном случае уравнение упругого режима имеет вид
. (6.32)
Область течения нефти в плоском пласте разбивается на множество ячеек с размерами Dх, Dу и h соответственно по осям х, у и z. Рассмотрим ячейку А, которая при бесконечном дроблении (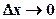
, 
) превращается в точку А. Будем считать, что в этой ячейке давление равно pij. При замене в уравнении (6.32) бесконечно малых приращений конечными выражения для производных преобразуются следующим образом
;
;
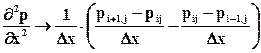; (6.33)
;
.
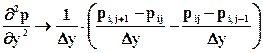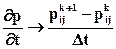Подставляя (6.33) в дифференциальное уравнение (6.32), получаем
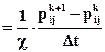. (6.34)
Здесь 
– давление в ячейке А в момент времени t;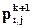 
– давление в той же ячейке в момент времени 
.
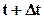Граничные и начальные условия при решении задач численными методами также приводят к соответствующей конечно-разностной форме. Соотношение (6.34) представляет собой алгебраическое уравнение. Таким образом, при использовании конечно-разностных методов вместо дифференциальных решают алгебраические уравнения.
Последнее соотношение представляет собой алгебраическое уравнение. Подобные соотношения можно составить для каждой ячейки, двигаясь по узлам сетки.
Граничные и начальные условия при решении задач численными методами также приводят к соответствующей конечно-разностной форме. Учёт граничных условий состоит в том, что если в узел попадает граница, то значение функции на границе попадает в молекулу, а если пересечение сетки с границей не в узле, то используются специальные аппроксимационные молекулы. Схематично это можно проиллюстрировать на следующем рисунке.
Методы решения соответствуют методам решения больших систем алгебраических уравнений, разработанных в специальных разделах математики.
Устойчивость решения – это воспроизводимость его при разных путях решения, используемых молекул и методов решения алгебраических уравнений, шаге сетки и шаге времени.
Так, для уравнения пьезопроводности
при 
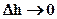, если 
и тогда погрешность вычислений будет порядка h2.
Это, в принципе, все те немногие сведения и примеры, которые достаточно знать для того, чтобы представлять, что такое численные методы и как они могут использоваться при решении задач разработки месторождений.
Аналоговые методы
Одним из методов решения задач теории фильтрации при разработке месторождений является метод аналогового моделирования. Его основой является математическая аналогия записи основных моделей разных процессов. Согласно закону Ома, для силы тока ix и iy в направлениях х и у имеем выражения
; 
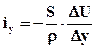, (6.35)
где S – площадь поперечного сечения электрического проводника; r – удельное электрическое сопротивление; DU – приращение электрического напряжения.
Сравним выражения (6.35) с формулой закона Дарси, представленной в конечно-разностной форме. Имеем
; 
. (6.36)
Выражения (6.35) и (6.36) совпадают, если давление жидкости заменить электрическим напряжением, скорости фильтрации – силой электрического тока, a 
– величиной 
. Указанные взаимно заменяемые величины – аналоги друг друга. Так, сила тока – аналог скорости фильтрации, электрическое напряжение – аналог давления, электрическая проводимость – аналог фильтрационной проводимости.
Следовательно, если написать
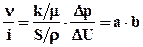, отсюда 
;
(6.37)
; 
,
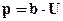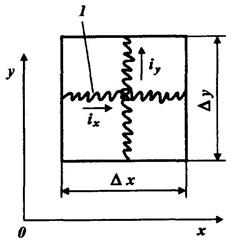
где а и b – коэффициенты пропорциональности, которые позволяют, проводя измерения тока и напряжения, получить соответствующие параметры фильтрации.
В случае двумерной фильтрации имеем аналоговую ячейку.
Рисунок 6.5 – Ячейка А: 1 – электрические сопротивления
В случае упругого режима аналогом коэффициента сжимаемости пласта b является электрическая емкость С. Можно записать:
; 
; 
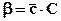, (6.38)
где а, b и с – коэффициенты пропорциональности.
Тогда
(6.39)
и уравнение пьезопроводности можно записать в виде
; 
. (6.40)
Следовательно, собрав соответствующую электрическую цепь для ячейки пласта с соответствующими k и m сопротивлениями и конденсаторами между ячейками, получим электрогидродинамическую аналогию (ЭГДА) поля пьезопроводности.
Процессы, описываемые уравнением (6.40), можно моделировать на специальных устройствах, называемых электроинтеграторами, подключая к каждой ячейке соответствующие электрические сопротивления и электрические емкости. По формулам (6.39) проводим пересчёт электрических параметров, экспериментально определяемых на электроинтеграторах, на соответствующие фильтрационные параметры. Электроинтеграторы позволяют моделировать задачу пьезопроводности. При этом граничные и начальные условия моделируются для давлений в виде напряжений, а потоки – в виде токов.
В настоящее время в связи со стремительным ростом производительности и объёмов памяти ЭВМ ЭГДА используют достаточно редко, так как для больших размеров и широкого диапазона вариации свойств создание ЭГДА весьма трудоёмко и дорого.
Модель пласта с модифицированными относительными
Проницаемостями
Относительные проницаемости – важнейшие характеристики, определяющие внутрипластовые потоки нефти, воды и газа, а, следовательно, обводненность продукции, текущую и конечную нефтеотдачу пластов.
Исходные измерения относительных проницаемостей производят на лабораторных установках путем осуществления фильтрации соответствующих флюидов через образцы пород пласта. Однако эти измерения относительных проницаемостей производятся на выбуренных из пласта образцах пород, имеющих, естественно, небольшие размеры. Так, диаметры и длины образцов цилиндрической формы составляют всего несколько сантиметров. При компьютерных расчётах разработки пластов приходится использовать конечно-разностные ячейки размером по площади пласта 
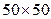м, 
м,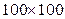 
м и более, в зависимости от размеров объекта разработки, требуемой точности расчётов и вычислительных возможностей компьютеров. При указанных выше размерах вычислительных ячеек потоки внутри них нефти, воды и газа будут значительно более сложными, чем потоки в образцах пород, изучаемых в лабораторных условиях, из-за значительно большей неоднородности пород, охватываемых конечно-разностной ячейкой. Также нельзя использовать неоднородность породы в ее образце-керне при расчётах разработки реальных пластов. Так, например, если площадь разрабатываемого объекта составляет 50 км2 (
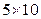км2 или 
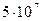м2), а толщина 10 м, то его объём составит 
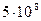м3 или 
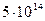с