Свойства неопределенного интеграла (свойства первообразной).
1. 
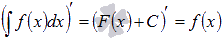
Производная результата интегрирования равна подынтегральной функции.
2. 
Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.
3. 
, где k – произвольная константа.
Коэффициент можно выносить за знак неопределенного интеграла.
4. 
Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.
2) Основные методы интегрирования.
1. Метод разложения, или непосредственное интегрирование –основан на применении свойств 3, 4 неопределенного интеграла.
2. Метод замены переменной –основан на использовании формулы
где z –новая переменная, связанная с x соотношением 
, 
непрерывная монотонная функция, имеющая непрерывную производную. Справедливость этой формулы следует из того, что равны дифференциалы ее левой и правой частей (проверьте).
3. Метод интегрирования по частям.
Если 
и 
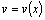–функции, имеющие непрерывные производные, то 
, тогда 
; проинтегрировав это равенство и учитывая свойство 2 неопределенного интеграла, получим формулу интегрирования по частям:
Иногда эту формулу приходится применять последовательно несколько раз.
3) Понятие определенного интеграла, его свойства.
Определённым интегралом от непрерывной функции f (x) на конечном отрезке [ a, b ] (где 
) называется приращение какой-нибудь её первообразной на этом отрезке.
Свойства определённого интеграла
Теорема 1. Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е.
Это свойство содержится в самом определении определённого интеграла. Однако его можно получить и по формуле Ньютона-Лейбница:
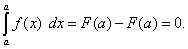
Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования, т.е.
(40)
Пусть F (x) – первообразная для f (x). Для f (t) первообразной служит та же функция F (t), в которой лишь иначе обозначена независимая переменная. Следовательно,
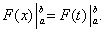
На основании формулы (39) последнее равенство означает равенство интегралов
и
Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла, т.е.
(41)
Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций, т.е.
(42)
Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если
то
(43)
Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е.
(44)
Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке 
внутри его, т.е.
(45)
Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
Теорема 9. Если верхний предел интегрирования больше нижнего и функции 
и 
непрерывны, то неравенство
можно почленно интегрировать, т.е.
(46)
Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.
4) Интеграл с переменным верхним пределом. Основная формула интегрального исчисления.
Пусть на отрезке [ a, b ] задана непрерывная функция f (x), тогда для любого x 
[ a, b ] существует функция:
задаваемая интегралом с переменным верхним пределом, стоящим в правой части равенства.
На интеграл с переменным верхним пределом распространяются все правила и свойства определённого интеграла.
Основная формула интегрального исчисления позволяет сводить вычисление определенного интеграла к вычислению значений первообразной (неопределенного интеграла) с использованием всего развитого аппарата вычислений неопределенных интегралов.
5) Замена переменной и формула интегрирования по частям в определенном интеграле.
6) Геометрические приложения определенного интеграла.
7) Понятие несобственного интеграла.
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий.
· Область интегрирования является бесконечной. Например, является бесконечным промежутком {\displaystyle [a,+\infty)} 
.
· Функция {\displaystyle f(x)} является неограниченной в окрестности некоторых точек области интегрирования.
Если интервал {\displaystyle [a,b]} конечный и функция интегрируема по Риману, то значение несобственного интеграла совпадает с значением определённого интеграла.
8) Евклидово пространство Е^n. Понятие функции нескольких переменных.
9) Предел и непрерывность функций нескольких переменных.
10) Частные производные функции нескольких переменных. Понятие дифференциала функции нескольких переменных.
11) Производная сложной функции нескольких переменных.
12) Частные производные и дифференциалы высших порядков функции нескольких переменных.
13) Понятие и необходимые условия локального экстремума функций нескольких переменных.
14) Достаточное условие локального экстремума функции нескольких переменных.
15) Понятие квадратичной функции. Критерии…
16) Достаточное условие локального экстремума ф-ии нескольких переменных. (частные случаи для ф-ий 2-х переменных ƶ=ϕ(x,y))
17) Понятие условного экстремума функции нескольких переменных.
18) Сведения к задаче о безусловном экстремуме. Метод множителей Лагранжа.
19) Достаточное условие условного экстремума для ф-ии 2-х переменных {ƶ=f(x,y) g(x,y)=c