Понятие предела последовательности
Постановка задачи. Пользуясь определением предела последовательности, доказать, что

План решения.
1. По определению число  называется пределом числовой последовательности
называется пределом числовой последовательности 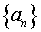 , если
, если 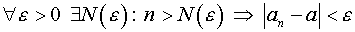 .
.
Это означает, что  неравенство
неравенство  имеет решение
имеет решение  .
.
2. Находим, при каких  справедливо неравенство
справедливо неравенство
 ,
,
т.е. решаем это неравенство относительно  .
.
3. Если решение имеет вид  , то
, то  – предел числовой последовательности
– предел числовой последовательности 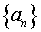 .
.
Замечание. Если решение неравенства  нельзя представить в виде
нельзя представить в виде  , то число
, то число  не является пределом последовательности.
не является пределом последовательности.
Задача 1. Доказать, что  (указать
(указать  ).
).

Покажем, что для любого 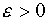 существует такой номер
существует такой номер  , что
, что  для всех
для всех  .
.
 .
.
 .
.
Из последнего неравенства следует, что можно выбрать  (квадратные скобки означают целую часть) и при любых
(квадратные скобки означают целую часть) и при любых  будет выполняться неравенство
будет выполняться неравенство  . Значит, по определению предела последовательности
. Значит, по определению предела последовательности
 .
.
Вычисление пределов вида 
Постановка задачи. Вычислить предел
 ,
,
где
 ,
,
 .
.
План решения.
Здесь  – многочлен степени
– многочлен степени 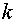 (бесконечно большая последовательность порядка
(бесконечно большая последовательность порядка 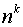 ) и
) и  – многочлен степени
– многочлен степени  (бесконечно большая последовательность порядка
(бесконечно большая последовательность порядка  ).
).
1. Вынесем в числителе множитель 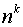 , получим
, получим 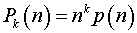 , где
, где  .
.
2. Вынесем в знаменателе множитель  , получим
, получим  , где
, где  .
.
3. Имеем
 .
.
4. Получаем, что
если  , то
, то  ;
;
если  , то
, то  ;
;
если  , то по теореме о пределе частного
, то по теореме о пределе частного
 .
.
Задача 2. Вычислить пределы числовых последовательностей.

Вычисление пределов вида 
Постановка задачи. Вычислить предел
 ,
,
где  – бесконечно большая последовательность порядка
– бесконечно большая последовательность порядка  и
и  – бесконечно большая последовательность порядка
– бесконечно большая последовательность порядка  (
( ).
).
План решения.
1. Вынесем в числителе множитель  , получим
, получим  , где
, где  .
.
2. Вынесем в числителе множитель  , получим
, получим  , где
, где  .
.
3. Имеем
 .
.
4. Получаем, что
если  , то
, то  ;
;
если  , то
, то  ;
;
если  , то по теореме о пределе частного
, то по теореме о пределе частного
 .
.
Задача 3. Вычислить пределы числовых последовательностей.

Вычисление пределов вида
Постановка задачи. Вычислить предел
 ,
,
где  – бесконечно большая последовательность порядка
– бесконечно большая последовательность порядка  и
и  – бесконечно большая последовательность порядка
– бесконечно большая последовательность порядка  (
( ).
).
План решения.
1. Вынесем в числителе множитель  , получим
, получим  , где
, где  .
.
2. Вынесем в числителе множитель  , получим
, получим  , где
, где  .
.
3. Имеем
 .
.
4. Получаем, что
если  , то
, то  ;
;
если  , то
, то  ;
;
если  , то по теореме о пределе частного
, то по теореме о пределе частного
 .
.
Замечание. Иногда необходимо привести выражение, стоящее после знака предела, к соответствующему виду.
Задача 4. Вычислить пределы числовых последовательностей.

Вычисление пределов вида
Постановка задачи. Вычислить предел
 ,
,
где  – бесконечно большая последовательность порядка
– бесконечно большая последовательность порядка  и
и  – бесконечно большая последовательность порядка
– бесконечно большая последовательность порядка  (
( ).
).
План решения.
1. Вынесем в числителе множитель  , получим
, получим  , где
, где  .
.
2. Вынесем в числителе множитель  , получим
, получим  , где
, где  .
.
3. Имеем
 .
.
4. Получаем, что
если  , то
, то  ;
;
если  , то
, то  ;
;
если  , то по теореме о пределе частного
, то по теореме о пределе частного
 .
.
Замечание. Иногда необходимо привести выражение, стоящее после знака предела, к соответствующему виду.
Задача 5. Вычислить пределы числовых последовательностей.

Вычисление пределов вида 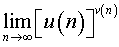
Постановка задачи. Вычислить предел последовательности
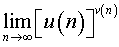 ,
,
где 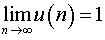 и
и  .
.
План решения.
1. Преобразуем выражение под знаком предела так, чтобы использовать второй замечательный предел, т.е. выделим единицу:
 ,
,
где  – бесконечно малая последовательность при
– бесконечно малая последовательность при  . Так как
. Так как  при
при  , то
, то
 .
.
2. Если  (
( ) и
) и  , то
, то
 .
.
Следовательно, если существует предел
 ,
,
то окончательно имеем
 .
.
Задача 6. Вычислить пределы числовых последовательностей.

Понятие предела функции
Постановка задачи. Пользуясь определением предела функции в точке, доказать, что
 .
.
План решения.
Число  называется пределом функции
называется пределом функции 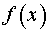 в точке
в точке  , если
, если 
 :
:  . Это значит, что
. Это значит, что  неравенство
неравенство  имеет решение
имеет решение  .
.
Задача 7. Доказать (найти 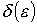 ), что:
), что:

Здесь функция  не определена при
не определена при  .
.
Необходимо доказать, что при произвольном 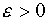 найдется такое
найдется такое 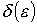 , что будет выполняться неравенство
, что будет выполняться неравенство
 , (1)
, (1)
если  . Но при
. Но при 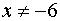 неравенство (1) эквивалентно неравенству
неравенство (1) эквивалентно неравенству

или
 . (2)
. (2)
Таким образом, при произвольном 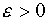 неравенство (1) будет выполняться, если будет выполняться неравенство (2) (здесь
неравенство (1) будет выполняться, если будет выполняться неравенство (2) (здесь  ). А это значит, что заданная функция при
). А это значит, что заданная функция при 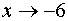 имеет пределом число
имеет пределом число 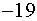 .
.
Понятие непрерывности функции в точке
Постановка задачи. Пользуясь определением, доказать, что функция 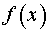 непрерывна в точке
непрерывна в точке  .
.
План решения.
Функция 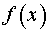 называется непрерывной в точке
называется непрерывной в точке 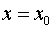 , если
, если 
 :
:  . Это значит, что
. Это значит, что  неравенство
неравенство 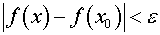 имеет решение
имеет решение 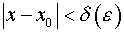 .
.
Задача 8. Доказать, что функция 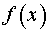 непрерывна в точке
непрерывна в точке  (найти
(найти  ).
).
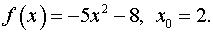
Покажем, что при любом 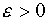 найдется такое
найдется такое  , что
, что 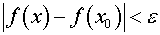 при
при 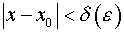 .
.
Имеем
 .
.
Следовательно
 ,
,
 .
.
Т.е. неравенство 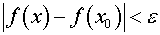 выполняется при
выполняется при  .
.
Вычисление пределов вида
Постановка задачи. Вычислить предел
 ,
,
где
 ,
,
 .
.
План решения.
1. Возможны три случая.
1) Если  , то функция
, то функция  непрерывна в точке
непрерывна в точке  и
и
 .
.
2) Если  и
и  , то
, то
 .
.
3) Если  и
и  , то разлагая многочлены на множители, получаем
, то разлагая многочлены на множители, получаем
 ,
,
где  и
и  .
.
2. Поскольку в определении предела функции при  аргумент не может принимать значение, равное
аргумент не может принимать значение, равное  , то в последнем случае можно сократить множитель
, то в последнем случае можно сократить множитель  . Получаем
. Получаем
 .
.
Замечание. Если число  является кратным корнем многочленов
является кратным корнем многочленов  и
и 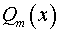 , то
, то  ,
, 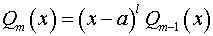 и
и
 ,
,
где  и
и 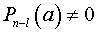 . В зависимости от чисел
. В зависимости от чисел 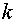 и
и  получим один из трех перечисленных в первом пункте случаев.
получим один из трех перечисленных в первом пункте случаев.
Задача 9. Вычислить пределы функций.

Вычисление пределов вида 
Постановка задачи. Вычислить предел
 ,
,
где 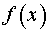 и
и 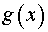 – бесконечно малые функции в точке
– бесконечно малые функции в точке  .
.
План решения.
Способ 1. Непосредственное вычисление пределов.
В зависимости от примера необходимо воспользоваться приемом домножения числителя и знаменателя на сопряженное выражение (если в дроби присутствуют радикалы) либо одной из следующих формул, приведя предварительно выражение к соответствующему виду:
 ,
,
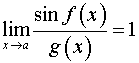 (первый замечательный предел),
(первый замечательный предел),
 (второй замечательный предел),
(второй замечательный предел),
 ,
,
 ,
,
 .
.
Во всех приведенных выше формулах  при
при  .
.
Способ 2. Замена на эквивалентные бесконечно малые.
1. Нужно заменить 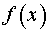 и
и 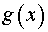 на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки
на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки  . Поэтому сначала сделаем замену переменной
. Поэтому сначала сделаем замену переменной  и будем искать предел при
и будем искать предел при  (если
(если  , то замену делать не надо).
, то замену делать не надо).
2. Преобразуем выражение под знаком предела, пользуясь алгебраическими и тригонометрическими формулами, и заменяем в произведении и частном бесконечно малые функции эквивалентными.
Таблица эквивалентных бесконечно малых:
| Функция | Эквивалентная бесконечно малая |

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|
Задача 10. Вычислить пределы функций.
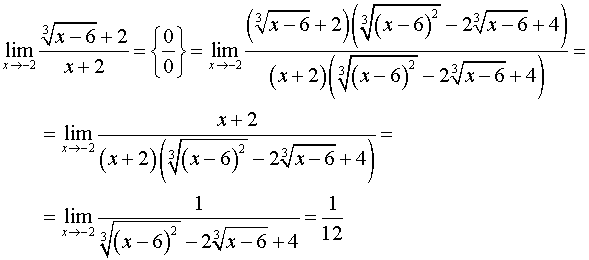
Вычисление пределов вида 
Постановка задачи. Вычислить предел
 ,
,
где 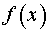 и
и 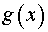 – бесконечно малые функции в точке
– бесконечно малые функции в точке  .
.
План решения.
Способ 1. Непосредственное вычисление пределов.
В зависимости от примера необходимо воспользоваться приемом домножения числителя и знаменателя на сопряженное выражение (если в дроби присутствуют радикалы) либо одной из следующих формул, приведя предварительно выражение к соответствующему виду:
 ,
,
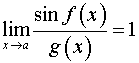 (первый замечательный предел),
(первый замечательный предел),
 (второй замечательный предел),
(второй замечательный предел),
 ,
,
 ,
,
 .
.
Во всех приведенных выше формулах  при
при  .
.
Способ 2. Замена на эквивалентные бесконечно малые.
1. Нужно заменить 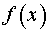 и
и 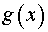 на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки
на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки  . Поэтому сначала сделаем замену переменной
. Поэтому сначала сделаем замену переменной  и будем искать предел при
и будем искать предел при  (если
(если  , то замену делать не надо).
, то замену делать не надо).
2. Преобразуем выражение под знаком предела, пользуясь алгебраическими и тригонометрическими формулами, и заменяем в произведении и частном бесконечно малые функции эквивалентными.
Таблица эквивалентных бесконечно малых:
| Функция | Эквивалентная бесконечно малая |

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|
Задача 11. Вычислить пределы функций.
Способ 1.

Способ 2.

Вычисление пределов вида 
Постановка задачи. Вычислить предел
 ,
,
где 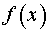 и
и 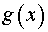 – бесконечно малые функции в точке
– бесконечно малые функции в точке  .
.
План решения.
Способ 1. Непосредственное вычисление пределов.
В зависимости от примера необходимо воспользоваться приемом домножения числителя и знаменателя на сопряженное выражение (если в дроби присутствуют радикалы) либо одной из следующих формул, приведя предварительно выражение к соответствующему виду:
 ,
,
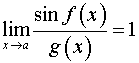 (первый замечательный предел),
(первый замечательный предел),
 (второй замечательный предел),
(второй замечательный предел),
 ,
,
 ,
,
 .
.
Во всех приведенных выше формулах  при
при  .
.
Способ 2. Замена на эквивалентные бесконечно малые.
1. Нужно заменить 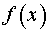 и
и 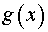 на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки
на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки  . Поэтому сначала сделаем замену переменной
. Поэтому сначала сделаем замену переменной  и будем искать предел при
и будем искать предел при  (если
(если  , то замену делать не надо).
, то замену делать не надо).
2. Преобразуем выражение под знаком предела, пользуясь алгебраическими и тригонометрическими формулами, и заменяем в произведении и частном бесконечно малые функции эквивалентными.
Таблица эквивалентных бесконечно малых:
| Функция | Эквивалентная бесконечно малая |

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|
Задача 12. Вычислить пределы функций.
Способ 1.

Способ 2.

Вычисление пределов вида 
Постановка задачи. Вычислить предел
 ,
,
где 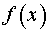 и
и 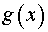 – бесконечно малые функции в точке
– бесконечно малые функции в точке  .
.
План решения.
Способ 1. Непосредственное вычисление пределов.
В зависимости от примера необходимо воспользоваться приемом домножения числителя и знаменателя на сопряженное выражение (если в дроби присутствуют радикалы) либо одной из следующих формул, приведя предварительно выражение к соответствующему виду:
 ,
,
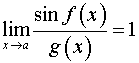 (первый замечательный предел),
(первый замечательный предел),
 (второй замечательный предел),
(второй замечательный предел),
 ,
,
 ,
,
 .
.
Во всех приведенных выше формулах  при
при  .
.
Способ 2. Замена на эквивалентные бесконечно малые.
1. Нужно заменить 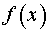 и
и 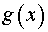 на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки
на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки  . Поэтому сначала сделаем замену переменной
. Поэтому сначала сделаем замену переменной  и будем искать предел при
и будем искать предел при  (если
(если  , то замену делать не надо).
, то замену делать не надо).
2. Преобразуем выражение под знаком предела, пользуясь алгебраическими и тригонометрическими формулами, и заменяем в произведении и частном бесконечно малые функции эквивалентными.
Таблица эквивалентных бесконечно малых:
| Функция | Эквивалентная бесконечно малая |

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|
Задача 13. Вычислить пределы функций.
Способ 1.
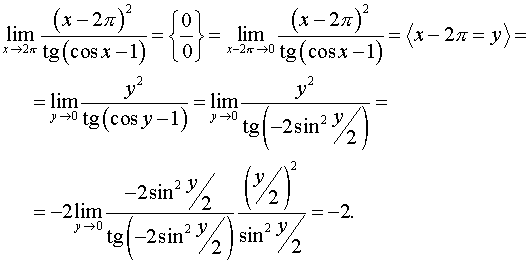
Способ 2.

Вычисление пределов вида 
Постановка задачи. Вычислить предел
 ,
,
где 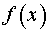 и
и 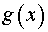 – бесконечно малые функции в точке
– бесконечно малые функции в точке  .
.
План решения.
Способ 1. Непосредственное вычисление пределов.
В зависимости от примера необходимо воспользоваться приемом домножения числителя и знаменателя на сопряженное выражение (если в дроби присутствуют радикалы) либо одной из следующих формул, приведя предварительно выражение к соответствующему виду:
 ,
,
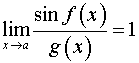 (первый замечательный предел),
(первый замечательный предел),
 (второй замечательный предел),
(второй замечательный предел),
 ,
,
 ,
,
 .
.
Во всех приведенных выше формулах  при
при  .
.
Способ 2. Замена на эквивалентные бесконечно малые.
1. Нужно заменить 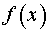 и
и 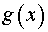 на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки
на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки  . Поэтому сначала сделаем замену переменной
. Поэтому сначала сделаем замену переменной  и будем искать предел при
и будем искать предел при  (если
(если  , то замену делать не надо).
, то замену делать не надо).
2. Преобразуем выражение под знаком предела, пользуясь алгебраическими и тригонометрическими формулами, и заменяем в произведении и частном бесконечно малые функции эквивалентными.
Таблица эквивалентных бесконечно малых:
| Функция | Эквивалентная бесконечно малая |

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|
Задача 14. Вычислить пределы функций.
Способ 1.

Способ 2.

Вычисление пределов вида 
Постановка задачи. Вычислить предел
 ,
,
где 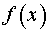 и
и 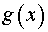 – бесконечно малые функции в точке
– бесконечно малые функции в точке  .
.
План решения.
Способ 1. Непосредственное вычисление пределов.
В зависимости от примера необходимо воспользоваться приемом домножения числителя и знаменателя на сопряженное выражение (если в дроби присутствуют радикалы) либо одной из следующих формул, приведя предварительно выражение к соответствующему виду:
 ,
,
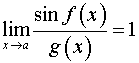 (первый замечательный предел),
(первый замечательный предел),
 (второй замечательный предел),
(второй замечательный предел),
 ,
,
 ,
,
 .
.
Во всех приведенных выше формулах  при
при  .
.
Способ 2. Замена на эквивалентные бесконечно малые.
1. Нужно заменить 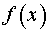 и
и 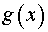 на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки
на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки  . Поэтому сначала сделаем замену переменной
. Поэтому сначала сделаем замену переменной  и будем искать предел при
и будем искать предел при  (если
(если  , то замену делать не надо).
, то замену делать не надо).
2. Преобразуем выражение под знаком предела, пользуясь алгебраическими и тригонометрическими формулами, и заменяем в произведении и частном бесконечно малые функции эквивалентными.
Таблица эквивалентных бесконечно малых:
| Функция | Эквивалентная бесконечно малая |

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|
Задача 15. Вычислить пределы функций.
Способ 1.

Способ 2.

Вычисление пределов вида
Постановка задачи. Вычислить предел
 ,
,
где  и
и  .
.
План решения.
Способ 1.
С помощью некоторых преобразований приводим предел ко второму замечательному пределу.
Способ 2.
1. Преобразуем выражение под знаком предела:
 .
.
2. Поскольку показательная функция 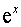 непрерывна, то можно перейти к пределу под знаком этой функции. Имеем
непрерывна, то можно перейти к пределу под знаком этой функции. Имеем
 .
.
3. Вычисляем предел показателя
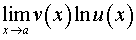
одним из перечисленных выше способов и записываем окончательный ответ.
Замечание. Оба способа по своей с