ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ПЕРЕМЕННЫЙ ТОК
С момента открытия факта, что всякий ток порождает магнитное поле (Эрстед, 1820 г.) делались многочисленные попытки вызвать обратное явление – возбудить ток в контуре (в замкнутой цепи) с помощью магнитного поля. Эта задача была решена Фарадеем, открывшим в 1831 г. явление электромагнитной индукции.
Явление состоит в следующем: при изменении потока магнитной индукции через площадь, ограниченную любым проводящем контуром, в этом контуре возникает электрический ток. Этот ток называется индукционным. При этом явление совершенно не зависит от способа изменения потока магнитной индукции.
Поток магнитной индукции Ф определяется соотношением:
Ф = B·S·cosα, (1)
где В – индукция магнитного поля, [В] = Тл; S – площадь поверхности, ограниченной контуром, [S] = м2; α – угол, который образует нормаль к плоскости контура с направлением вектора индукция магнитного поля  , [α] = рад; [Ф] = Вб.
, [α] = рад; [Ф] = Вб.
Как видно из соотношения (1), возбудить индукционный ток мо-жно либо путём изменения величины индукция магнитного поля – В, либо изменением геометрической формы контура, т.е. площади, либо изменением его положения в пространстве, т.е. изменением угла α.
Ленц (1833 г.) установил общее правило для определения направления индукционного тока: индуцированный в контуре ток имеет такое направление, что его собственное магнитное поле компенсирует изменение потока магнитной индукции через плоскость контура, которое вызвало этот индукционный ток. Это правило является следствием закона сохранения энергии и подтверждается опытами. Величина электродвижущей силы индукции ξ i равна скорости изменения потока магнитной индукции, взятой со знаком минус:
 . (2)
. (2)
Данное выражение называется законом Фарадея. Знак минус математически выражает правило Ленца.
Из закона Фарадея можно дать определение единице потока магнитной индукции – Веберу: если поток магнитной индукции через площадь, ограниченную контуром, изменяется на 1Вб за 1 сек, то в контуре индуцируется ЭДС, равная 1В.
В случае явления электромагнитной индукции имеет место превращение одних видов энергии в другие. При изменении геометрии контура (например, с квадрата на окружность) механическая энергия превращается в энергию электрического индукционного тока. В свою очередь энергия электрического тока превращается в тепловую, нагревая проводник, образующий контур.
Какова же природа ЭДС индукции?
 ЭДС индукции обусловлена силой Лоренца, если м-поле неподвижно (рис.3) и обусловлена вихревым электрическим полем, возникшим в результате изменяющегося м-поля (рис.4). Вихревое эл. поле не отличается от электростатического поля электрических зарядов по своему действию на электрический заряд
ЭДС индукции обусловлена силой Лоренца, если м-поле неподвижно (рис.3) и обусловлена вихревым электрическим полем, возникшим в результате изменяющегося м-поля (рис.4). Вихревое эл. поле не отличается от электростатического поля электрических зарядов по своему действию на электрический заряд  в данной точке пространства. Но по своей структуре, т.е. в целом, эти поля резко отличаются друг от друга. Электростатическое поле имеет “источники поля” – электрические заряды. Линии напряжённости его не замкнуты. В этом поле работа по перемещению заряда между двумя фиксированными точками зависит только от положения этих точек, но не от формы пути. Электрическое поле э-м. индукции (вихревое поле) не имеет источников. Линии напряжённости этого поля замкнуты подобно линиям м-поля. Работа по замкнутому контуру не равна 0.
в данной точке пространства. Но по своей структуре, т.е. в целом, эти поля резко отличаются друг от друга. Электростатическое поле имеет “источники поля” – электрические заряды. Линии напряжённости его не замкнуты. В этом поле работа по перемещению заряда между двумя фиксированными точками зависит только от положения этих точек, но не от формы пути. Электрическое поле э-м. индукции (вихревое поле) не имеет источников. Линии напряжённости этого поля замкнуты подобно линиям м-поля. Работа по замкнутому контуру не равна 0.
ЯВЛЕНИЕ САМОИНДУКЦИИ
Магнитное поле контура, в котором сила тока изменяется, индуцирует ток не только в других контурах, но и в себе самом. Это явление получило название самоиндукции.
Опытным путём установлено, что магнитный поток вектора магнитной индукции поля, создаваемого текущим в контуре током, пропорционален силе этого тока:
Ф = LI, (3)
где L – индуктивность контура. Постоянная характеристика контура, которая зависит от его формы и размеров, а так же от магнитной проницаемости среды, в которой находится контур. [L] = Гн (Генри,
1Гн = Вб/А).
Если за время dt ток в контуре изменится на dI, то магнитный поток, связанный с этим током, изменится на dФ = LdI в результате чего в этом контуре появится ЭДС самоиндукции:
 . (4)
. (4)
Знак минус показывает, что ЭДС самоиндукции (а, следовательно, и ток самоиндукции) всегда препятствует изменению силы тока, который вызвал самоиндукцию.
Наглядным примером явления самоиндукции служат экстратоки замыкания и размыкания, возникающие при включении и выключении электрических цепей, обладающей значительной индуктивностью.
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
Магнитное поле обладает потенциальной энергией, которая в момент его образования (или изменения) пополняется за счёт энергии тока в цепи, совершающего при этом работу против ЭДС самоиндукции, возникающей вследствие изменения поля.
Работа dA за бесконечно малый промежуток времени dt, в течении которого ЭДС самоиндукции  и ток I можно считать постоянными, равняется:
и ток I можно считать постоянными, равняется:
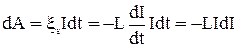 . (5)
. (5)
Знак минус указывает, что элементарная работа совершается током против ЭДС самоиндукции. Чтобы определить работу при изменении тока от 0 до I, проинтегрируем правую часть, получим:
 . (6)
. (6)
Эта работа численно равна приросту потенциальной энергии ΔWп магнитного поля, связанного с этой цепью, т.е. A = -ΔWп.
Выразим энергию магнитного поля через его характеристики на примере соленоида. Будем считать, что магнитное поле соленоида однородно и в основном расположено внутри его. Подставим в (5) значение индуктивности соленоида, выраженное через его параметры и значение силы тока I, выраженное из формулы индукции магнитного поля соленоида:
 , (7)
, (7)
где N – общее число витков соленоида; ℓ – его длина; S – площадь сечения внутреннего канала соленоида.
 , (8)
, (8)
После подстановки имеем:
 . (9)
. (9)
Разделив обе части на V, получим объёмную плотность энергии поля:
 (10)
(10)
или, с учётом, что  получим,
получим, 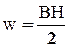 . (11)
. (11)
ПЕРЕМЕННЫЙ ТОК