Занятие 7
ОСНОВЫРЕГРЕССИОННОГО АНАЛИЗА
Цель работы: изучить основные приёмы проведения регрессионного анализа с помощью функций MS Excel и с использованием инструмента Пакета анализа «Регрессия».
Регрессионный анализ – статистический метод исследования зависимости случайной величины Y от переменных 
(j = 1, 2,…, k), рассматриваемых как неслучайные величины. Зная уравнение регрессии, можно при любых значениях Х, подставляя их в уравнение, приближённо оценить значение Y. Объясняющие переменные 
рассматриваются как неслучайные величины независимо от истинного закона распределения, а случайная величина Y имеет нормальный закон распределения с условным математическим ожиданием, являющимся функцией от :
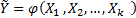
с постоянной, независящей от аргументов, дисперсией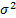 
.
Построение уравнения линейной регрессии
Пример 1. Построить уравнение линейной регрессии 
для следующих данных:
| x | |||||
| y | 1,9 | 1,7 | 1,8 | 1,5 | 1,3 |
Проверить значимость коэффициентов регрессии и уравнения регрессии. Построить доверительный интервал для генерального коэффициента βyx. Принять α = 0,05.
Решение.
Коэффициенты b 0 и b 1 вычисляются по формулам:
; 
Введём исходные данные в ячейки A2:A6 (значения x) и в ячейки B2:B6 (значения y).
Для вычисления коэффициентов линейной регрессии в MS Excel используется функция ЛИНЕЙН(известные_значения_y, известные_значения_х, конст, статистика).
Аргументы функции: известные_значения_ y: множество значений результативного признака Y; известные_значения_ x: множество значений факторных признаков Xi; конст: логическое значение, которое указывает, требуется ли, чтобы свободный член b0 был равен 0; если конст имеет значение ИСТИНА, или опущена, то коэффициент b0 вычисляется обычным образом; статистика ‒ логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии; если статистика имеет значение ИСТИНА, то функция ЛИНЕЙН рассчитывает дополнительную статистику.
Выделим диапазон A9:B9 и введём в него функцию: =ЛИНЕЙН(B2:B6;A2:A6;1;0). Нажмём комбинацию клавиш < Ctrl >+< Shift >+< Enter > и в ячейках A9 и B9 получим результат: -0,14 (b 1) и 2,2 (b 0) (рис.1). То есть, уравнение приближённой регрессии имеет вид: 
.
После того, как уравнение регрессии найдено, необходимо провести статистический анализ результатов, который заключается в проверке значимости всех коэффициентов уравнения регрессии в сравнении с ошибкой воспроизводимости и адекватности уравнения.
Для проверки значимости отдельных коэффициентов регрессии (выдвигаются гипотезы Н 0: b j=0) используется t -критерий Стъюдента, наблюдаемое значение которого находят по формуле:
,
Рис. 1.
,
где: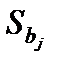 
- стандартная ошибка коэффициента уравнения регрессии bj. 
находится как корень квадратный из дисперсии соответствующего коэффициента регрессии:
; 
;
; 
.
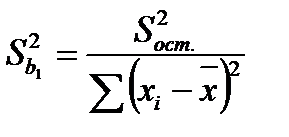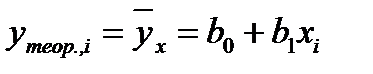Критическое значение tкр. находится с использованием функции СТЪЮДЕНТРАСПОБР для уровня значимости α и числа степеней свободы n - 2. Гипотеза Н 0 отвергается с вероятностью ошибки α, если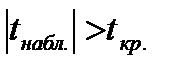 
. Из этого следует, что соответствующий коэффициент регрессии значим. В противном случае коэффициент регрессии незначим, и соответствующая переменная в модель не включается. Оставшиеся коэффициенты пересчитываются заново.
Выделим диапазон B11:С15 и введём в него формулу: =ЛИНЕЙН(B2:B6;A2:A6;1;1). Нажмём комбинацию клавиш < Ctrl >+< Shift >+< Enter > и в ячейках B11:С15 получим следующие результаты: в ячейке В11 ‒ коэффициент b 1, в ячейке С11 ‒ коэффициент b 0. В ячейках В12, С12 ‒ стандартные ошибки коэффициентов уравнения регрессии 
.
Для построенной модели вычисляется коэффициент детерминации:
‒ регрессионные остатки.
В ячейке С13 вычисляется стандартная ошибка регрессионных остатков по формуле:
В таблице также выводится сумма квадратов регрессии (ячейка В15) и сумма квадратов остатков (ячейка С15), которые вычисляются по формулам:
Рассчитаем дисперсию регрессии по формуле:
,
где: k ‒ число факторов.
В таблице приводится наблюдаемое значение критерия Фишера (ячейка В14), которое находится по формуле:
,
а также число степеней свободы остаточной дисперсии (ячейка С14).
Проверим значимость коэффициентов регрессии и самого уравнения.
Рассчитаем наблюдаемое значение критерия:
; 
.
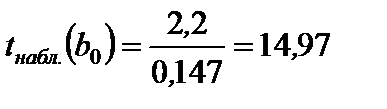Критическое значение найдём с помощью функции: СТЪЮДЕНТРАСПОБР(0,05;3). Результат: tкр. =3,182. Так как и для первого, и для второго коэффициента выполняется условие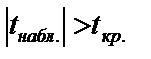 
, то оба коэффициента регрессии значимы.
Проверка значимости уравнения регрессии проводится с использованием критерия Фишера. Наблюдаемое значение критерия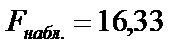 
. По уровню значимости α для числа степеней свободы df1=k и df2=n-k-1 находим критическое значение Fкр. с использованием функции: FРАСПОБР(0,05;1;3). Результат: Fкр. =10,13. Так как Fнабл. > Fкр., то нулевая гипотеза Н 0 о незначимости отклоняется и уравнение признаётся значимым.
Найдём уравнение линейной регрессии с использованием инструмента Пакета анализа «Регрессия ».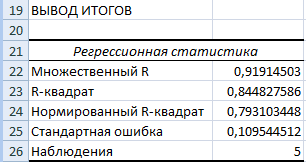 
Вызовем инструмент «Регрессия» и в диалоговом окне введём следующие данные: Входной интервал Y: $B$2:$B$6; Входной интервал Х: $А$2:$А$6; Выходной интервал: $А$19; отметим галочками все пункты в разделе Остатки. Нажмём кнопку Ок. Результат состоит из четырёх таблиц и 2-х графиков.
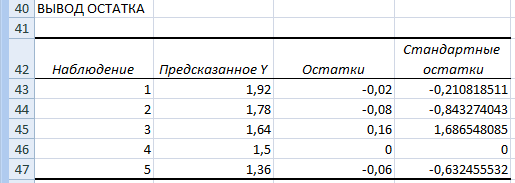
Доверительный интервал приведён в ячейках F36:G36.
Пример 2. Построить уравнение регрессии 
по следующим данным:
| X | 5,1 | 7,5 | 5,6 | 5,6 | 5,4 | 6,7 | 6,9 | 7,7 | 6,6 | 6,5 | 6,3 | 7,2 |
| Y | 0,9 | 15,9 | 11,5 | 0,0 | 0,8 | 7,2 | 7,2 | 15,7 | 0,6 | 13,5 | 13,2 | 15,1 |
Проверить значимость коэффициентов регрессии и уравнения регрессии. Построить доверительный интервал для генерального коэффициента βyx. Найти доверительные границы для уравнения регрессии и построить соответствующие графики. Принять α=0,05. Указание: при решении задачи использовать функции MS Excel.
Решение.
Записать исходные данные в диапазон А2:В13 (рис.3). В ячейках А1:С1 и D2:D13 ввести для наглядности обозначения.
В ячейку Е2 ввести формулу:
=(СУММ(А2:А13)*СУММ(В2:В13)-12*СУММПРОИЗВ(А2:А13;В2:В13))/
(СУММ(А2:А13)^2-12*СУММКВ(А2:А13)).
В ячейку Е3 ввести формулу:
=СРЗНАЧ(В2:В13)-Е2*СРЗНАЧ(А2:А13).
В ячейках Е2, Е3 получатся коэффициенты уравнения регресси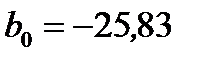и 
и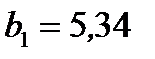 
. Уравнение регрессии имеет вид:
.
В ячейки Е4:Е16 ввести формулы, как показано в таблице.
| D | E | |
| xср. = | =СРЗНАЧ(А2:А13) | |
| yср. = | = СРЗНАЧ(В2:В13) | |
| s2 ост.= | =СУММКВРАЗН(С2:С13;В2:В13)/10 | |
| sb1 = | =КОРЕНЬ(Е6/СУММ((А2:А13-Е4)^2)) | |
| sb0 = | =КОРЕНЬ(Е6*СУММКВ(А2:А13)/(12*CУММКВ(А2: А13)-CУММ(А2:А13)^2)) | |
| tb1 = | =ABS(E2)/E7 | |
| tb0 = | = ABS(E3)/E8 | |
| tкрит. | =СТЪЮДРАСПРОБР(0,05;10) | |
| F = | =10*СУММ((С2:С13-Е5)^2)/СУММ((C2:C13-B2:D13)^2) | |
| Fкрит. = | =FРАСПОБР(0,05;1;10) | |
| Дов. инт. для betayx | ||
| нижн. гран. | =E2-E11*E7 | |
| верх. гран. | =E2+E11*E7 |
Указание. После ввода формул в ячейки Е7 и Е12 следует нажать комбинацию клавиш Ctrl+Shift+Enter, так как используются формулы массива.
Результаты вычислений представлены в таблице.