Физический смысл производной.
Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:
8. Дифференциал функции, его геометрический смысл, применение в приближенных вычислениях.Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).
Это записывается так:
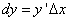
или
или же
Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину 
(см. рисунок).
Почему дифференциал можно использовать в приближенных вычислениях?
Дифференциал, 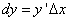является главной, линейной относительно 
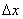частью приращения функции; чем меньше 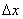, тем большую долю приращения составляет эта часть. В этом можно убедиться, мысленно передвигая перпендикуляр, опущенный из точки P (см. рисунок) к оси Ox, ближе к началу координат. Поэтому при малых значениях 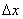(и при 
) приращение функции можно приближенно заменить его главной частью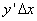 
, т.е.
О разных формах записи дифференциала
Дифференциал функции в точке x и обозначают
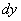
или
Следовательно,
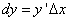(1)
или
, (2)
поскольку дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.
9. Исследование функции на экстремумы, необходимое и достаточное условия экстремума. Точка 
называется точкой максимума (минимума) функции 
,если существует такая окрестность точки , что для всех 
из этой окрестности выполняется неравенство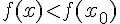 
, 
. На рис.9 изображены точки: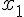 
- точка максимума, 
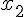- точка минимума.
Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Минимум или максимум функции называется экстремумом функции.
Рассмотрим условия существования экстремума функции.
Необходимое и достаточные условия существования экстремумов функции одной переменной
Из теоремы Ферма следует, что если х = х0 точкаэкстремума, то производная в этой точке равна нулю
f /(x0) =0.
Следует также отметить, что, иногда, в точке экстремума функция может быть недифференцируемой, т.е. в этой точке производная не существует.
- Необходимое условие существования экстремума функции: если х = х0 - точка экстремума, то f /(x0) =0 или f /(x0) не существует.
Точки, в которых f /(x0) обращается в нуль или не существует, называется критическими.
- Достаточное условие существования экстремума функции: если функция y=f(x) непрерывна в точке х = х0 и ее окрестности, дифференцируема в этой окрестности, кроме, быть может, самой точки, и производная
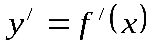при переходе через точку х = х0 меняет свой знак, то функция имеет экстремум при х = х0.
При этом х = х0 - точка максимума, если знак меняется с «+ » на «- », и х = х0 - точка минимума, если знак меняется с «- » на «+ ».
10. Исследование функции на выпуклость и вогнутость, точки перегиба графика функции. График дифференцируемой функции 
называется выпуклым (или выпуклым вниз) на интервале xÎ(a;b), если он расположен выше любой касательной, проведенной к графику на этом интервале.
График функции называется вогнутым (или выпуклым вверх) на интервале xÎ(a;b), если он расположен ниже любой касательной, проведенной к графику на этом интервале.
Точка графика непрерывной функции , отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
В простейших случаях область определения функции можно разбить на конечное число интервалов с постоянным направлением выпуклости.
При xÎ(a;х0) график вогнутый, при xÎ(х0;b) выпуклый, М0(х0;y0) – точка перегиба.
Достаточное условие выпуклости, вогнутости.
Если функция 
является дважды дифференцируемой и ее 
сохраняет знак при всех xÎ(a;b), то график функции имеет постоянное направление выпуклости на этом интервале:
при <0 – выпуклость вверх (вогнутость),
при >0 – выпуклость вниз, или просто выпуклость.
Необходимое условие для точки перегиба.
Если x0 – абсцисса точки перегиба графика функции , то 
или 
не существует.
Необходимое условие не является достаточным. Точки, принадлежащие графику функции , в которых или не существует, называются подозрительными на перегиб.
Достаточное условие для точек перегиба.
Если вторая производная при переходе через точку х0, подозрительную на перегиб, изменяет знак, то точка графика с абсциссой х0 является точкой перегиба. Если не изменяет знак при переходе через точку х0, то перегиба нет.
11. Асимптоты кривых. Схема полного исследования функции и построение графика. Асимптоты функции
Асимптотой функции называют прямую, к которой приближаются точки графика функции при бесконечном удалении их от начала координат.
Вертикальные асимптоты
Вертикальные асимптоты определяются точками разрыва функции и границами области определения. График функции, непрерывной на всей числовой прямой, вертикальных асимптот не имеет. Некоторые особенности поведения функции в окрестности вертикальных асимптот представлено на рисунке. Вертикальные асимптоты определяются точками разрыва второго рода В этом случае f (x 0 ± 0) = ± ∞, или f (x 0 ± 0) = + ∞, или f (x 0 ± 0) = − ∞. Следует отметить, что в этом случае может отмечаться всё разнообразие поведения функции в окрестности точки разрыва. Например, на рис. 8.2 приведён график элементарной функции
. 
Рис. 8.2. Точка разрыва второго рода для данной функции определяется только справа